bzoj3561 莫比乌斯反演

DZY Loves Math VI

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 518  Solved: 344
[Submit][Status][Discuss]

Description

给定正整数n,m。求

 

 

Input

一行两个整数n,m。

Output

一个整数，为答案模1000000007后的值。

Sample Input

5 4

Sample Output

424

HINT

数据规模：

1<=n,m<=500000，共有3组数据。

Source

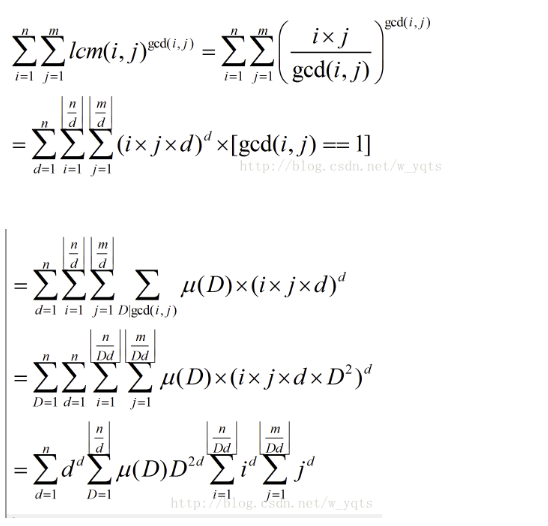
 #pragma GCC optimize(2)
 #pragma G++ optimize(2)
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstdio>
 #include<cstring>

 #define ll long long
 #define inf 1000000000
 #define mod 1000000007
 #define N 500007
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')f=-;ch=getchar();}
     while(isdigit(ch)){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int n,m,ans,tot;
 int miu[N],p[N];
 int a[N],sum[N];
 bool flag[N];

 void prepration()
 {
     miu[]=;
     for (int i=;i<=n;i++)
     {
         if (!flag[i]){p[++tot]=i;miu[i]=-;}
         for (int j=;j<=tot&&p[j]*i<=n;j++)
         {
             flag[i*p[j]]=;miu[i*p[j]]=-miu[i];
             if (i%p[j]==){miu[i*p[j]]=;break;}
         }
     }
 }
 inline int mul(int x,int y)
 {
     if (y==) return x;
     int t=mul(x,y>>);
     t=(ll)t*t%mod;
     if (y&) t=(ll)t*x%mod;
     return t;
 }
 int main()
 {
     n=read();m=read();if (n<m) swap(n,m);
     prepration();
     for (int i=;i<=n;i++) a[i]=;
     for (int d=;d<=m;d++)
     {
         int x=mul(d,d),y=;
         for (int i=;i<=n/d;i++)
         {
             a[i]=(ll)a[i]*i%mod;sum[i]=(sum[i-]+a[i])%mod;
         }
         for (int D=;D<=n/d;D++)if (miu[D])
         {
             int t=mul(D,*d);
             y=(y+(ll)t*miu[D]%mod*sum[n/d/D]%mod*sum[m/d/D]%mod)%mod;
         }
         ans=(ans+(ll)x*y%mod)%mod;
     }
     printf("%d",ans);
 }