Laplace算子和Laplacian矩阵

1 Laplace算子的物理意义

Laplace算子的定义为梯度的散度。

在Cartesian坐标系下也可表示为：

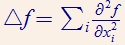
或者，它是Hessian矩阵的迹：

以热传导方程为例，因为热流与温度的梯度成正比，那么温度的梯度的散度就是热量的损失率。

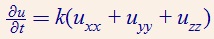
由此可见，Laplace算子可用于表现由于物质分布不均引起的物质输送。

2 Laplace算子的数学意义

现在，在一维空间中简单分析上面的式子：

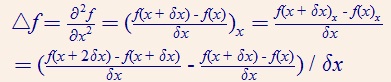
也可以写作：

把分子第一项和第二项分别按泰勒展开：

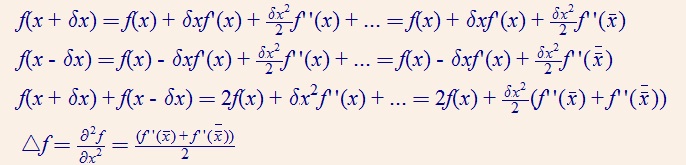
可以看出Laplace算子实际上是一个使函数取平均的算子。多维空间相似。

3 Laplace方程

若Laplace算子右边为零，称为Laplace方程。Laplace方程的解称为调和函数。若右边是一个函数，称为泊松方程。

4 Laplace算子在图像处理的运用

图像处理是以像素作为基础离散化，如下：

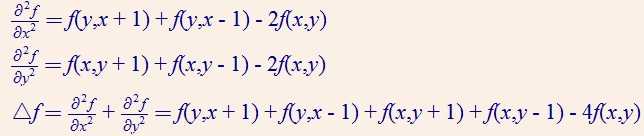
5 Laplacian 矩阵

是一种用于表示图的矩阵。 它的维度是 |V|-by-|V| ( |V| 是节点的数目 )。 James Demmel提供了一种由Incidence matrix转化为Laplacian矩阵的方法。

In(G)是一个 |V|-by-|E| 矩阵( |E| 是边的数目 ), 设边e=(i,j)，这一列除了第i行（为+1）和第j行(为-1)外都为零。 需要说明的是，根据这个定义，对于无向图 e=(i,j) 和 e=(j,i) 是等价的， 看似会生成很多不同的In图（根据每条边不同的取向）。但是实际上可以证明，无论边的方向怎么取，由In图生成的L图都是唯一的。 也就是说， e=(i,j) 和 e=(j,i) 怎么取是无关紧要的。 如何使用In图生成L图：

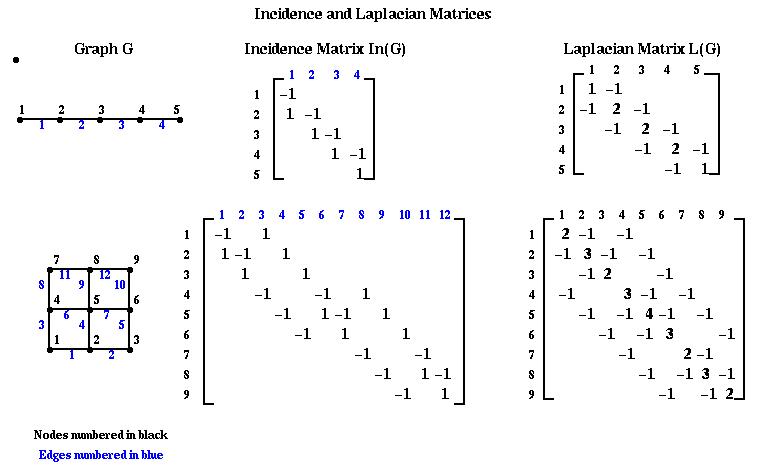
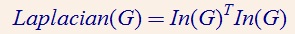
可得知Laplacian矩阵的两个重要性质：一是为对称阵。二是存在一个为零的特征值（秩为|V|-1）。三是一个半正定矩阵。 注意Laplace算子是负定的。

在求解含Laplacian矩阵的方程组时，常常要求为正定矩阵。观察发现这是因为Laplacian矩阵每列相加等于零。这时只需要手动更改第一行和第一列（比如第一个元素设为1，其余设为零），破坏其结构，令秩等于|V|就可以了。

对于非正定矩阵，左乘个transpose of the matrix, 推导如下：

Ax – b = 0

最小化 ||Ax – b||^2，展开后对x求导数：

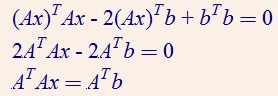
可转化为正定方程组。

6 Laplace算子和Laplacian矩阵的关系

Laplace算子可以推广到多维情况计算。Laplacian矩阵主要用于三维以下的图形学计算，可以表现复杂的几何结构。而Lapace方程使用了Laplace算子来表示Laplacian矩阵。