Kuhn-Munkres算法 (剪辑)（备用）

KM算法是通过给每个顶点一个标号（叫做顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。

设顶点Xi的顶标为A[i]，顶点Yi的顶标为B[i]，顶点Xi与Yj之间的边权为w[i,j]。

在算法执行过程中的任一时刻，对于任一条边(i,j)， A[i]+B[j]>=w[i,j]始终成立。KM算法的正确性基于以下定理：
　　若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图（概念很重要））有完备匹配，那么这个完备匹配就是二分图的最大权匹配。
　　这个定理是显然的。因为对于二分图的任意一个匹配，如果它包含于相等子图，那么它的边权和等于所有顶点的顶标和（显然这是最大的）；如果它有的边不包含于相等子图，那么它的边权和小于所有顶点的顶标和。所以相等子图的完备匹配一定是二分图的最大权匹配。
　　初始时为了使A[i]+B[j]>=w[i,j]恒成立，令A[i]为所有与顶点Xi关联的边的最大权，B[j]=0。如果当前的相等子图没有完备匹配，就按下面的方法修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止。
　　我们求当前相等子图的完备匹配失败了，是因为对于某个X顶点，我们找不到一条从它出发的交错路。这时我们获得了一棵交错树（概念很重要），它的叶子结点全部是X顶点。现在我们把交错树中X顶点的顶标全都减小某个值d，Y顶点的顶标全都增加同一个值d，那么我们会发现：
1.两端都在交错树中的边(i,j)，A[i]+B[j]的值没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。
2.两端都不在交错树中的边(i,j)，A[i]和B[j]都没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。（意思是说，对于整个图而言，如果不属于相等子图，则还不属于相等子图，如果属于相等子图，因为不变，所以还属于相等子图）
3.X端不在交错树中，Y端在交错树中的边(i,j)，它的A[i]+B[j]的值有所增大。它原来不属于相等子图，现在仍不属于相等子图。d应该等于min{A[i]+B[j]-w[i,j]|Xi在交错树中，Yi不在交错树中}。

举个简单的例子：

已知K5,5的权矩阵为
y1 y2 y3 y4 y5
x1 3 5 5 4 1
x2 2 2 0 2 2
x3 2 4 4 1 0
x4 0 1 1 0 0
x5 1 2 1 3 3

初始化：其中K5,5的顶划分为X={xi},Y={yi},i=1,2,3,4,5.
(1)取可行顶标l(v)为
l(yi)=0,i=1,2,3,4,5；l(x1)=max(3,5,5,4,1}=5,l(x2)=max{2,2,0,2,2}=2,l(x3)=max(2,4,4,1,0}=4,l(x4)=max{0,1,1,0,0}=1,l(x5)=max{1,2,1,3,3}=3.
(2) Gl及其上之匹配见图7.12。

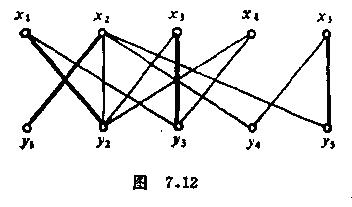
这个图中ο(G-x2)=3,由Tutte定理知无完备匹配。需要修改顶标。

Tutte定理：一个图G有完备匹配，其充要条件是，对于图中任意点集U，去掉U后剩下的具有奇数个顶点的连通分量个数（记作o(G-U)）不超过U中的顶点数。
当相等子图中U={x2}，去掉U后有三个连通分量{y1}, {x1,x3,x4,y2,y3}, {x5,y4,y5}，均为奇数个顶点，故o(G-x2)=3，比U中的顶点数1大。所以相等子图没有完备匹配。
(3)
找交错树。对于x4中，交错树有：x1-y2-x4和x1-y2-x3-y3-x4.则需要找的d就是从在交错树中的x集合（1,3,4）和不在交错树种
的y集合（1,4,5）中去lx[i]+ly[j]-map[i][j]的最小值。得到的值为1.则x1,x2,x3,x4,x5的顶标分别修改成
4,2,3,0,3；y1,y2,y3,y4,y5的顶标分别修改成0,1,1,0,0。

修改之后发现可以进入相等子图的边有(x1,y4), (x4,y1), (x4,y4), (x4,y5)

然后我们在刚才基础上继续寻找交错树，我们可以发现交错树有多种情况：

1.x4-y4

2.x4-y5

3.x4-y1-x2-y4

4.x4-y2-x1-y4

这样我们找到的完备匹配分别是：

1.x1-y2,x2-y1,x3-y3,x4-y4,x5-y5.

2.x1-y2,x2-y1,x3-y3,x4-y5,x5-y4.

3.x1-y2,x2-y4,x3-y3,x4-y1,x5-y5.

4.x1-y4,x2-y1,x3-y3,x4-y2,x5-y5.

对应的最大权值分别为：

1.5+2+4+0+3=14

2.5+2+4+0+3=14

3.5+2+4+0+3=14

4.4+2+4+1+3=14

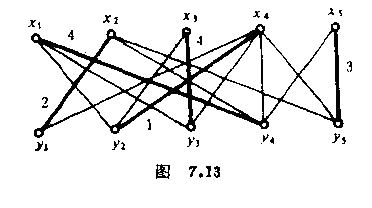
(4) 用修改后的顶标l得Gl及其上面的一个完备匹配如图7.13（第四种情况）。图中粗实线给出了一个最佳匹配，其最大权是4+2+4+1+3=14

　　以上就是KM算法的基本思路。但是朴素的实现方法，时间复杂度为O(n4)——需要找O(n)次增广路，每次增广最多需要修改O(n)次顶标，每次修改顶标时由于要枚举边来求d值，复杂度为O(n2)。
实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数slack，每次开始找增广路时初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack[j]变成原值与A[i]+B[j]-w[i,j]的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有的slack值都减去d。（else后面的是因为Lx[i］变小了d
而slack[j] = min{Lx[i] + Ly[j] -w[i][j]} 所以slack[j](j不属于T)受影响也要减小d）