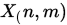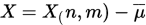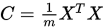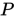PCA降维技术
PCA降维技术
Time: 2017-2-28
主成分分析(PCA)
主成分分析(Principal Component Analysi)是一种掌握可以提取主要特征对的方法,它可以从多元失误中解析出主要影响因素。计算朱成福的目的是将高维数据投影到低维空间。主要是用于降维,提取数据的主要特征分量。
降维,当然以为着信息的丢失,但是鉴于数据本身常常存在相关性,我们可以想办法在降维的同时将信息的随时尽量降低。
PCA Algorithm
主要思想:
利用较少数据的特征对样本进行描述以达到降低特征空间维数的目的,根据样本点在多维空间的位置分布,以样本点在空间中变化最大方向,即方差最大方向,作为差别矢量来实现数据的特征提取。具体可以参考这篇文章 关于K-L变换的部分。
在PCA中,我们要做的是找到一个方向向量,当我们把所有的数据都投射到该向量上时,我们希望投射的平均均方误差尽可能的小。方向向量是一个经过原点的向量,而投射误差是从特征向量向该方向向量垂线的长度。大致的情形如下图

具体步骤:
step 1. 数据:
step 2. 零均值化
step 3. 计算出协方差矩阵
step 4. 计算出协方差矩阵的特征值与特征向量, 可以使用SVD分解来实现
step 5. 取特征值最大的前K个特征向量组成矩阵
step 6. 计算PCA:, Y为降维后的结果
在step 2, 对原始数据进行均值化处理后,不仅消除了指标量纲和数量的影响,而且能更加全面地反映原始数据中各指标的变异程度和相互影响程度的信息
而关于协方差矩阵主要是因为,对于
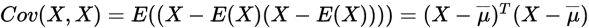 ,当计算自相关(
,当计算自相关(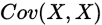 )而协方差计算的主要是数据的相关性质,所以我们可以减少相关性,从而来实现对数据的降维。关于为什么需要使用协方差矩阵可以看这篇文章
)而协方差计算的主要是数据的相关性质,所以我们可以减少相关性,从而来实现对数据的降维。关于为什么需要使用协方差矩阵可以看这篇文章需要注意的是PCA主要是减少投射的平均均方误差,这里需要和线性回归做区别,线性回归主要减少的是最小均方误差。如下图

实例
假设有5条数据,两个特征属性,矩阵的形式如下:

按照上面的算法来实现:
[1]

[2] 均值化:我们可以知道

[3] 计算协方差矩阵

[4] 求特征值 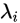 以及特征向量可得
以及特征向量可得
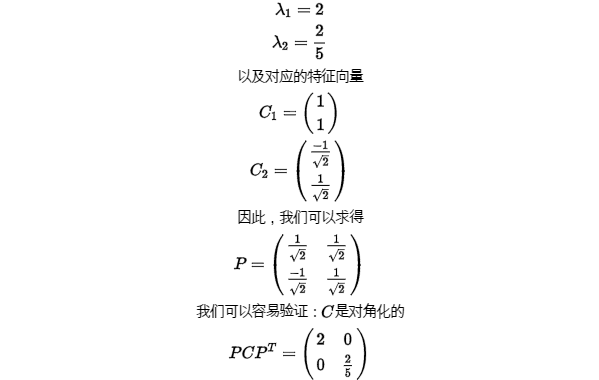
[5] 这里我们取最大的一列,可得到
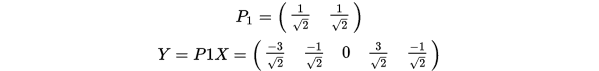
最后我们得到了最终的降维结果如下图

为了更好的观察,把Andrew Ng的课件图拿了过来:

PCA降维技术的更多相关文章
- 机器学习算法-PCA降维技术
机器学习算法-PCA降维 一.引言 在实际的数据分析问题中我们遇到的问题通常有较高维数的特征,在进行实际的数据分析的时候,我们并不会将所有的特征都用于算法的训练,而是挑选出我们认为可能对目标有影响的特 ...
- 降维技术---PCA
数据计算和结果展示一直是数据挖掘领域的难点,一般情况下,数据都拥有超过三维,维数越多,处理上就越吃力.所以,采用降维技术对数据进行简化一直是数据挖掘工作者感兴趣的方向. 对数据进行简化的好处:使得数据 ...
- [机器学习之13]降维技术——主成分分析PCA
始终贯彻数据分析的一个大问题就是对数据和结果的展示,我们都知道在低维度下数据处理比较方便,因而数据进行简化成为了一个重要的技术.对数据进行简化的原因: 1.使得数据集更易用使用.2.降低很多算法的计算 ...
- 数据降维技术(2)—奇异值分解(SVD)
上一篇文章讲了PCA的数据原理,明白了PCA主要的思想及使用PCA做数据降维的步骤,本文我们详细探讨下另一种数据降维技术—奇异值分解(SVD). 在介绍奇异值分解前,先谈谈这个比较奇怪的名字:奇异值分 ...
- 利用PCA降维
参考:<机器学习实战>- Machine Learning in Action 一. 基本思想 PCA(Principal Component Analysis),主成分分析.是目前应用 ...
- 一步步教你轻松学主成分分析PCA降维算法
一步步教你轻松学主成分分析PCA降维算法 (白宁超 2018年10月22日10:14:18) 摘要:主成分分析(英语:Principal components analysis,PCA)是一种分析.简 ...
- 用PCA降维 (Principal Component Analysis,主成分分析)
参考资料:Mastering Machine Learning With scikit-learn 降维致力于解决三类问题.第一,降维可以缓解维度灾难问题.第二,降维可以在压缩数据的同时让信息损失最 ...
- 机器学习(十六)— LDA和PCA降维
一.LDA算法 基本思想:LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的.这点和PCA不同.PCA是不考虑样本类别输出的无监督降维技术. 我们要将数据在低维度上进行投影,投 ...
- [综] PCA降维
http://blog.json.tw/using-matlab-implementing-pca-dimension-reduction 設有m筆資料, 每筆資料皆為n維, 如此可將他們視為一個mx ...
随机推荐
- 10 Future Web Trends 十大未来互联网趋势
转载自:http://blog.sina.com.cn/s/blog_4be577310100ajpb.html 我们很满意自己进入的当前网络纪元,通常被称为Web 2.0.这个阶段互联网的特征包括搜 ...
- Apache上php项目简单部署
1.建一个简单的php项目 1)在目录C:\wamp\www中新建一个文件夹,命名为20151021 2)在文件夹20151021中新建一个index.php文件,内容为: <?php echo ...
- css 浮动问题详解
浮动(float),一个我们即爱又恨的属性.爱,因为通过浮动,我们能很方便地布局: 恨,浮动之后遗留下来太多的问题需要解决,特别是IE6-7(以下无特殊说明均指 windows 平台的 IE浏览器). ...
- codevs1253 超级市场(dp)
1253 超级市场 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description 某人喜欢按照自己的规则去市场买菜,他每天 ...
- ThreadLocal,静态变量,实例变量,局部变量的线程安全
之前都是业务层次开发,现在公司进行的网络编程,一下子要了解太多java底层的东西并进行应用,我现在边学习边应用.由于知识能力有限,在上次发博客时出现了一个小小的纰漏,而这个纰漏被细心的博友发现了. 首 ...
- Vue页面间传值,以及客户端数据存储
初学Vue,遇到了页面传值的问题,大概网上学习了解了一下,在此跟大家分享一下学习心得,欢迎批评指正. 一.参数传值 如果是简单的页面传值,比如传一个id到详情页等等,推荐使用参数传值. 这里页面是通过 ...
- 在PL/SQL中使用游标、动态sql和绑定变量的小例子
需求:查询并输出30号部门的雇员信息 方式一:使用 loop...fetch SET serveroutput ON; DECLARE CURSOR c_emp IS ; v_emp emp%rowt ...
- HEK_费用报表审核无审核权限,有些字段无法编辑的问题处理
Q:HEK_费用报表审核无审核权限,有些字段无法编辑的问题处理 A:设置AP员工->给AP员工分配审批权限->绑定员工和ERP账号 1.将审核人设置为AP员工 2.分配给员工审批权限 3. ...
- AI不与人为敌
业界广为流传着一句话:有多少人工就有多少智能. 其实还应该有一句话:有多少付出就因该有多少回报.公正是世界永恒的话题. 一.人工智能还是人工愚蠢 科技从来没有善恶,也不会杀人,愚蠢的人比聪明的人做的错 ...
- gitlab变更邮箱后发送邮件报SSLError错误
测试发送邮件: gitlab-rails console Notify.test_email('test666@example.com', 'Message Subject', 'Message Bo ...