Vladik and Entertaining Flags

Vladik and Entertaining Flags

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In his spare time Vladik estimates beauty of the flags.

Every flag could be represented as the matrix n × m which consists of positive integers.

Let's define the beauty of the flag as number of components in its matrix. We call component a set of cells with same numbers and between any pair of cells from that set there exists a path through adjacent cells from same component. Here is the example of the partitioning some flag matrix into components:

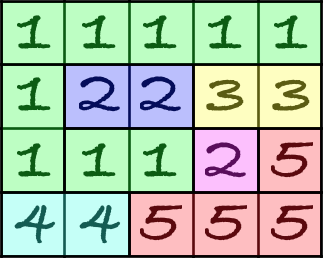
But this time he decided to change something in the process. Now he wants to estimate not the entire flag, but some segment. Segment of flag can be described as a submatrix of the flag matrix with opposite corners at (1, l) and (n, r), where conditions 1 ≤ l ≤ r ≤ m are satisfied.

Help Vladik to calculate the beauty for some segments of the given flag.

Input

First line contains three space-separated integers n, m, q (1 ≤ n ≤ 10, 1 ≤ m, q ≤ 105) — dimensions of flag matrix and number of segments respectively.

Each of next n lines contains m space-separated integers — description of flag matrix. All elements of flag matrix is positive integers not exceeding 106.

Each of next q lines contains two space-separated integers l, r (1 ≤ l ≤ r ≤ m) — borders of segment which beauty Vladik wants to know.

Output

For each segment print the result on the corresponding line.

Example

input

4 5 4
1 1 1 1 1
1 2 2 3 3
1 1 1 2 5
4 4 5 5 5
1 5
2 5
1 2
4 5

output

6
7
3
4

Note

Partitioning on components for every segment from first test case:

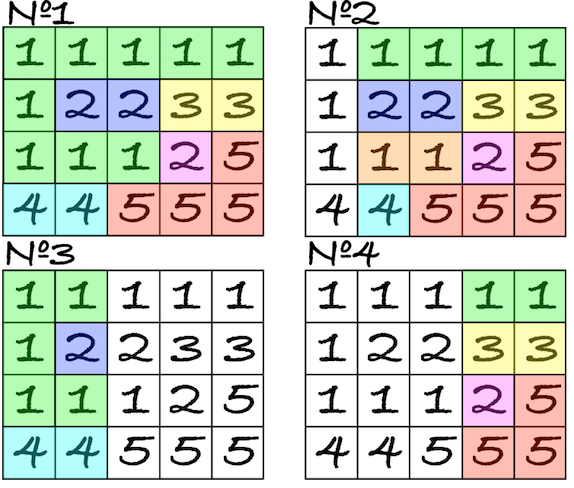
分析：给一个10*n矩阵，q次询问l到r内联通块个数；

　　　用线段树维护区间，每个节点维护左右两边即可，合并区间时使用”并查集“实现；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <bitset>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <cassert>
#include <ctime>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define sys system("pause")
#define ls rt<<1
#define rs rt<<1|1
const int maxn=1e5+;
const int N=2e5+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p%mod;p=p*p%mod;q>>=;}return f;}
int n,m,k,t,a[][maxn],fa[],id[];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
int Union(int x,int y)
{
    x=find(x),y=find(y);
    if(x==y)return ;
    return fa[x]=y,;
}
struct node
{
    int s[];
    int cnt;
}s[maxn<<];
void pup(node &s,node l,node r,int pos)
{
    s.cnt=l.cnt+r.cnt;
    for(int i=;i<=*n;i++)fa[i]=i,id[i]=;
    for(int i=;i<=n;i++)
    {
        if(a[i][pos]==a[i][pos+])s.cnt-=Union(l.s[i+n],r.s[i]+*n);
    }
    int cnt=;
    for(int i=;i<=n;i++)
    {
        int &x=id[find(l.s[i])];
        if(!x)x=++cnt;
        s.s[i]=x;
        int &y=id[find(r.s[i+n]+*n)];
        if(!y)y=++cnt;
        s.s[i+n]=y;
    }
    return ;
}
void build(int l,int r,int rt)
{
    if(l==r)
    {
        s[rt].cnt=;
        for(int i=;i<=n;i++)
        {
            if(a[i][l]!=a[i-][l])
            {
                s[rt].cnt++;
            }
            s[rt].s[i]=s[rt].s[i+n]=s[rt].cnt;
        }
        return ;
    }
    int mid=l+r>>;
    build(l,mid,ls);
    build(mid+,r,rs);
    pup(s[rt],s[ls],s[rs],mid);
}
node gao(int L,int R,int l,int r,int rt)
{
    if(L==l&&R==r)return s[rt];
    int mid=l+r>>;
    if(R<=mid)return gao(L,R,l,mid,ls);
    else if(L>mid)return gao(L,R,mid+,r,rs);
    else
    {
        node x=gao(L,mid,l,mid,ls);
        node y=gao(mid+,R,mid+,r,rs);
        node ret;
        pup(ret,x,y,mid);
        return ret;
    }
}
int main()
{
    int i,j;
    int q;
    scanf("%d%d%d",&n,&m,&q);
    rep(i,,n)rep(j,,m)scanf("%d",&a[i][j]);
    build(,m,);
    while(q--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",gao(l,r,,m,).cnt);
    }
    return ;
}