平衡树前置——BST
上一节:平衡树——序
BST(Binary Search Tree)二叉排序树,其定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:
①若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
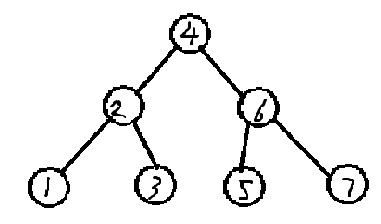
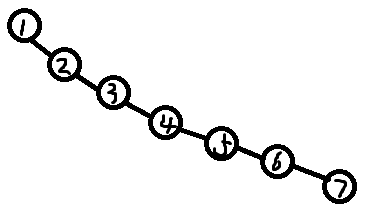
平衡树前置——BST的更多相关文章
- [luogu1110][ZJOI2007]报表统计【平衡树】
传送门 [洛谷传送门] [bzoj传送门] 前言 洛谷和网上的题解都好复杂哦,或者是stl水过. 窝的语文不怎么好,所以会有一些表达上的累赘或者是含糊不清,望各大佬海涵. 前置芝士 首先你一定要会平衡 ...
- 平衡树及笛卡尔树讲解(旋转treap,非旋转treap,splay,替罪羊树及可持久化)
在刷了许多道平衡树的题之后,对平衡树有了较为深入的理解,在这里和大家分享一下,希望对大家学习平衡树能有帮助. 平衡树有好多种,比如treap,splay,红黑树,STL中的set.在这里只介绍几种常用 ...
- skip跳跃表的实现
skiplist介绍 跳表(skip List)是一种随机化的数据结构,基于并联的链表,实现简单,插入.删除.查找的复杂度均为O(logN).跳表的具体定义, 跳表是由William Pugh发明的, ...
- skip list跳跃表实现
跳表(skip List)是一种随机化的数据结构,基于并联的链表,实现简单,插入.删除.查找的复杂度均为O(logN).跳表的具体定义,跳表是由William Pugh发明的,这位确实是个大牛,搞出一 ...
- 静态区间第k大 树套树解法
然而过不去你谷的模板 思路: 值域线段树\([l,r]\)代表一棵值域在\([l,r]\)范围内的点构成的一颗平衡树 平衡树的\(BST\)权值为点在序列中的位置 查询区间第\(k\)大值时 左区间在 ...
- mysql开发相关
1.mysql事务原理,特性,事务并发控制2.如何解决高并发场景下的插入重复3.乐观锁和悲观锁4.常用数据库引擎之间区别5.mysql索引6.B-Tree7.mysql索引类型8.什么时候创建索引9. ...
- BJOI2017 喷式水战改
题目链接. Description 维护一个序列,支持操作: 每次在 \(P_i\) 位置后插入一段 \(X_i\) 单位的燃料,这一段有三个模式,对应的能量分别是 \(A_i, B_i, C_i\) ...
- 关于二叉查找树的一些事儿(bst详解,平衡树入门)
最近刚学了平衡树,然后突发奇想写几篇博客纪念一下,可能由于是刚学的缘故,还有点儿生疏,望大家海涵 说到平衡树,就不得不从基础说起,而基础,正是二叉查找树 什么是二叉查找树?? 大家观察一下下面的这棵二 ...
- BST,Splay平衡树学习笔记
BST,Splay平衡树学习笔记 1.二叉查找树BST BST是一种二叉树形结构,其特点就在于:每一个非叶子结点的值都大于他的左子树中的任意一个值,并都小于他的右子树中的任意一个值. 2.BST的用处 ...
随机推荐
- click事件触发也有失灵的时候?
今天做了个手机页面,点击某个按钮->弹出菜单,再点击菜单以外的任意位置->关闭菜单,在其他浏览器里面没有问题,但是在IOS浏览器中并不会关闭. 网上解决这个bug的帖子很多,这篇帖子主要是 ...
- B1826 [JSOI2010]缓存交换 贪心+离散化+堆
这个题仔细一想可以直接贪心做,因为队列里下一个出现的早的一定最优.正确性显然.然后我只拿了50,我直接模拟另一个队列暴力修改最后一个点的nxt值,自然会T.但是其实不用修改,直接插入就行了前面的不影响 ...
- Java事件处理机制- 事件监听器的四种实现方式
自身类作为事件监听器 外部类作为事件监听器 匿名内部类作为事件监听器 内部类作为事件监听器 自身类作为事件监听器: import javax.swing.*; import java.awt.*; i ...
- [App Store Connect帮助]三、管理 App 和版本(2.1)输入 App 信息:查看和编辑 App 信息
在您添加 App 至您的帐户后,您也可以在“我的 App”部分查看和编辑 App 信息和平台版本信息. 在输入 App 信息前,请检查必填项.可本地化和可编辑属性.您在上传构建版本或提交您的 App ...
- BZOJ 1208 set
思路: 开俩set 模拟一下 就好了 //By SiriusRen #include <bits/stdc++.h> using namespace std; int n,xx,yy; s ...
- C#学习-执行存储过程
使用存储的优点 1.执行更快.直接写sql脚本会有个解析编译的过程. 2.修改方便.当业务改变时,只需要改存储过程,不需要修改C#代码 3.传递Sql脚本数据相对更小 缺点: 1.使用存储过程,数据库 ...
- 在Django中使用redis:包括安装、配置、启动。
一.安装redis: 1.下载: wget http://download.redis.io/releases/redis-3.2.8.tar.gz 2.解压 tar -zxvf redis-.tar ...
- bindColumn、bindParam与bindValue的区别
bindColumn:绑定一列到一个 PHP 变量(类似于list()函数为变量赋值) <?php //连接数据库函数 functionconnect() { try { $dbh = new ...
- 电源管理POWER_SUPPLY_PROP_CAPACITY_LEVEL
电量计节点中有capacity_level 节点,这个是反应当前电池电流高低水平的参数. 分为critical low full normal 一般是由fg的芯片来判断,通过IIC读取,具体判断可参考 ...
- Python初学1
windows版python下载: https://pan.baidu.com/s/1dsAPp0C9PJUF73kFDdAzXQ 安装时勾选pip和Add python.exe to Path. w ...
