zookeeper客户端命令行操作

一、命令行

（1）使用zookeeper安装bin目录下的./zkCli.sh连接到zookeeper服务器上，基本语法如下：

./zkCli.sh -timeout 0 -r -server ip:port

其中，-timeout表示当前会话的超时时间，zookeper依靠与客户端的心跳来判断会话是否有效，单位是毫秒

-r代表只读模式，zookeeper的只读模式指一个服务器与集群中过半机器失去连接以后，这个服务器就不在不处理客户端的请求，但我们仍然希望该服务器可以提供读服务。

-server，指定服务器ip地址和端口号

连接之前确保zookeeper开启

（2）h：查看帮助

（3）ls，列出某一节点下的子节点信息

（4）stat，查看节点的状态信息

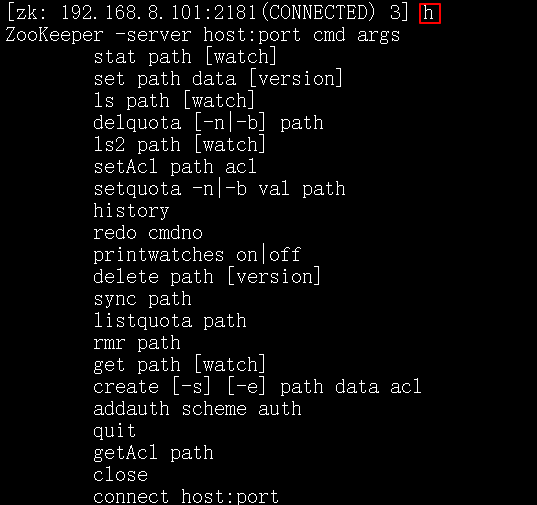
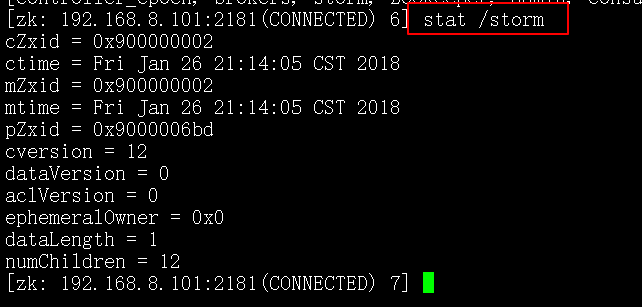
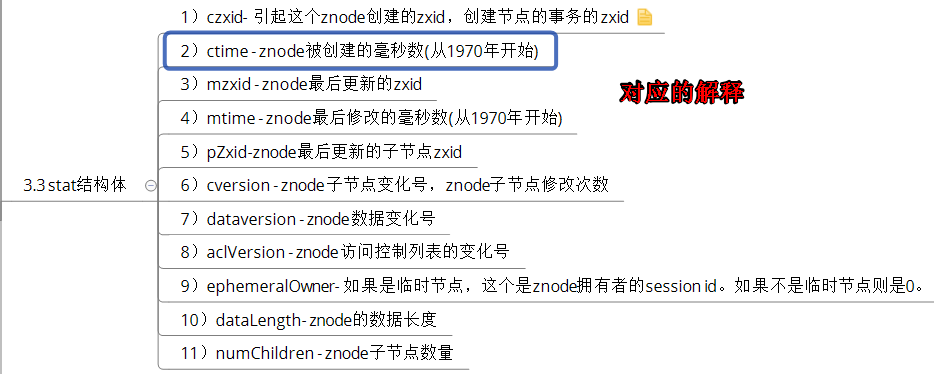
在zookeeper中，每一次对节点的写操作都认为是一次事务，每一个事务，系统都会分配一个唯一的事务ID，czxid代表该节点被创建的事务ID，ctime表示创建的时间，mzxid表示最后一次被更新的事务ID，mtime是修改时间，pzxid表示子节点列表最后一次被更新的事务ID，cversion子节点的版本号，dataversion数据版本号，aclversion权限版本号，ephemeralOwner用于临时节点，代表临时节点的事务ID，如果为持久节点则为0，dataLength代表节点存储的数据的长度，numChildren当前节点的子节点个数。

（5）get，获取当前节点存储的数据内容

（6）ls2，列出当前节点的子节点，同时列出节点状态

（6）create，创建节点

-s，顺序节点

-e，临时节点

（7）set，修改节点数据，可携带版本号

修改的时候要么不携带版本号，要么携带的版本号要跟dataVersion的版本号一致，否则就会报错（类似于乐观锁机制）。

（8）delete，删除节点，只能删除没有子节点的节点，要删除含有子节点的时候需使用rmr命令

（9）rmr，删除节点

（10）setquota，配额，给节点限制值，比如限制子节点个数、节点数据的长度

-n，限制子节点个数

-b，限制值的长度

当创建节点超出配额时，zookeeper不会抛出异常，会在zookeeper.out记录警告信息

（11）listquota，查看配额，以及节点的配额状态

（12）delquota，删除配额

（13）close，关闭当前连接

（14）history，查看历史执行指令

（15）redo，重复执行指令

参考地址:http://blog.sina.com.cn/s/blog_790c59140102w6ho.html