【模板】SPFA（不完全详解）

一种最短路求法（个人觉得比DIJKSTRA好用）

用于有向图。

大概思路：从根节点开始，枚举每一个点，同时更新他们所联通的点的最短路径，如果路径被更新，则把这个点入队，一直重复这个操作直到队伍为空为止。  

代码：

struct edge {
    int next, to, v;
}e[];//存图，next代表同一个头结点的下一条边 

void spfa(int S) {
    int p, x, y, l, r;
    for (x = ; x <= n; ++x)
        dis[x] = inf;
    q[] = S, dis[S] = , v[S] = ;//初始化
    for (l = r = ; l != (r + ) % N; ) {
        p = q[l], ++l %= N;//每次取出队首
        for (x = first[p]; x; x = e[x].next)//遍历与队首同头的每一条边
            if (dis[p] + e[x].v < dis[(y = e[x].to)]) {//如果可以更新
                dis[y] = dis[p] + e[x].v;//更新
                if (!v[y]) {
                    v[y] = ;
                    q[++r %= N] = y;//入队
                }
            }
        v[p] = ;
    }
}

但是这种做法容易被卡掉（神奇奶牛），所以可以采用SLF优化。

SLF优化：每一次都把即将入队的值与队首值比较，若比队首值小，则存入队首。

为什么呢？

因为每一次都会从队首开始遍历，当队首是最小值时，被更新的所以节点的值也会是最小值，这样可以节省很大一部分时间。

（有点抽象。。举个例子吧）

（我不想画图）

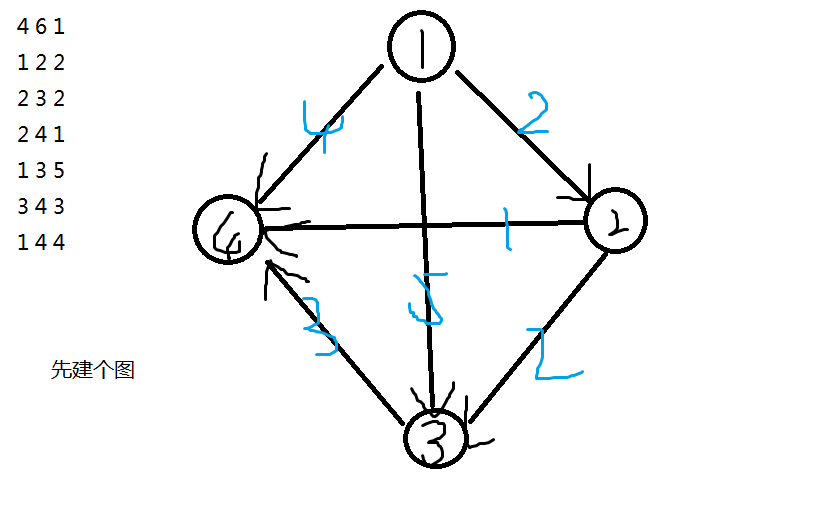
这里需要注意：只有dis[]存储路径值，q[]存储的是当前最小路径值所在的位置，包括edge里的next也是同一个起点的上一对点的序号。（这里的头就是First[]的下标）

这里各种各样的序号很多。。特别容易弄混。会把各种序号分段输出的程序放在结尾，看不懂的话试几组样例看看输出会很有帮助。

到这里只是第一次更新。

下面是第二次更新：

接下来就可以以此类推了。。如果看不懂的话下面是分段输出的代码，结合上面的图看，体会一下中心思想。

代码：

#include<iostream>
using namespace std;
struct edge {
    int next, to, v;
    edge(){}
    edge(int x,int y,int z)
    {
        next=x;
        to=y;
        v=z;
    }
}e[];

int first[];
int tot;
int dis[];
int q[];
int v[];
void add_edge(int x, int y,int z) {
    e[++tot] = edge(first[x], y,z);
    first[x] = tot;
}
int n;
int N=;

int inc(int x) {
    x = x + ;
    x = x % N;
    return x;
}

int dec(int x) {
    x = x -  + N;
    x = x % N;
    return x;
}

void spfa(int S) {
    int p, x, y, l, r;
    for (x = ; x <= n; ++x)
        dis[x] = 0x7ffff;
    q[] = S, dis[S] = , v[S] = ;
    for (l = r = ; l != (r + ) % N; ) {
        p = q[l];
        cout<<"从第"<<p<<"号边开始遍历"<<endl;
        l=inc(l);
        for (x = first[p]; x; x = e[x].next)
        {
            cout<<"这时是第"<<x<<"号边"<<endl;
            if (dis[p] + e[x].v < dis[(y = e[x].to)]) {
                cout<<"更新"<<" "<<"将"<<dis[y];
                dis[y] = dis[p] + e[x].v;
                cout<<"更新为"<<dis[y]<<endl;
                if (!v[y]) {
                    v[y] = ;
                    if (dis[y] < dis[q[l]])
                    {q[(l=dec(l))] = y;
                    cout<<"从队首插入"<<y<<endl;
                    cout<<"这时l为"<<l<<"r不变"<<endl;
                    }
                    else
                    {q[(r=inc(r))] = y;
                    cout<<"从队尾插入"<<y<<endl;
                    cout<<"这时l不变r变为"<<r<<endl; }
                    cout<<"更新后的队列为"<<endl;
                    for(int i=;i<=n;i++)
                    {
                    cout<<q[i]<<" ";
                    } cout<<endl;
                    cout<<"入队情况为"<<endl;
                    for(int i=;i<=n;i++)
                    cout<<"第"<<i<<"号元素"<<v[i]<<" ";
                    cout<<endl;
                }
            }
        }
        v[p] = ;
        cout<<"此时最短路径被更新为"<<endl;
        for(int i=;i<=n;i++)
        {
            cout<<dis[i]<<" ";
        }
        cout<<endl;
    }
}

int main()
{
    int m,S;
    cin>>n>>m>>S;
    int x,y,z;
    for(int i=;i<=m;i++)
    {
        cin>>x>>y>>z;
        add_edge(x,y,z);
    }

    spfa(S);
    cout<<"最终最短路径"<<endl;
    for(int i=;i<=n;i++)
    {
        cout<<dis[i]<<" ";
     } 

    cout<<"一共有"<<tot<<"个节点，分别是"<<endl;
    for(int i=;i<=tot;i++)
    {
        cout<<"与它同起点的上一对点为"<<e[i].next<<"号"<<" "<<"它指向"<<e[i].to<<"这个点"<<endl;
    }
    cout<<"下面输出First数组"<<endl;
        for(int i=;i<=tot;i++)
    {
        cout<<first[i]<<" ";
    }

}

这是举例用的样例：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
到这里就结束啦！希望可以看懂！
蒟蒻的第二篇博客（再放个烟花吧！）