Codeforces Round #454 D. Power Tower （广义欧拉降幂）

D. Power Tower

time limit per test

4.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is usually made of power-charged rocks. It is built with the help of rare magic by levitating the current top of tower and adding rocks at its bottom. If top, which is built from k - 1 rocks, possesses power p and we want to add the rock charged with power w**k then value of power of a new tower will be {w**k}p.

Rocks are added from the last to the first. That is for sequence w1, ..., w**m value of power will be

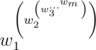
After tower is built, its power may be extremely large. But still priests want to get some information about it, namely they want to know a number called cumulative power which is the true value of power taken modulo m. Priests have n rocks numbered from 1 to n. They ask you to calculate which value of cumulative power will the tower possess if they will build it from rocks numbered l, l + 1, ..., r.

Input

First line of input contains two integers n (1 ≤ n ≤ 105) and m (1 ≤ m ≤ 109).

Second line of input contains n integers w**k (1 ≤ w**k ≤ 109) which is the power of rocks that priests have.

Third line of input contains single integer q (1 ≤ q ≤ 105) which is amount of queries from priests to you.

k**th of next q lines contains two integers l**k and r**k (1 ≤ l**k ≤ r**k ≤ n).

Output

Output q integers. k-th of them must be the amount of cumulative power the tower will have if is built from rocks l**k, l**k + 1, ..., r**k.

Example

input

Copy

6 10000000001 2 2 3 3 381 11 62 22 32 44 44 54 6

output

Copy

1124256327597484987

Note

327 = 7625597484987

思路：

因为euler( euler(x) ) <= x/2 所以在log（x）次内欧拉函数值就会降为1，并且一直为1.而任何数对1取模的答案都是0，所以我们可以遇见模数为1时就可以结束迭代，

• 因此每次询问最多迭代log（m）次，每一次迭代只需要一个快速幂的时间复杂度，也是log（m）

• 因此对于每一个询问综合的时间复杂度是O(log（m）^2)

  注意，在指数循环节中快速幂时，需要在ans>=mod时，取模后再加上mod，以此才满足欧拉降幂定理。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
ll mod(ll x, ll m)
{
    return x >= m ? x % m + m : x;
}
ll powmod(ll a, ll b, ll MOD)
{
    ll ans = 1;
    while (b)
    {
        if (b % 2)
            ans = mod(ans * a, MOD);
        // ans = ans * a % MOD;
        // a = a * a % MOD;
        a = mod(a * a, MOD);
        b /= 2;
    }
    return ans;
}

ll m;
int n;
int q;
ll a[maxn];
map<ll, ll> vis;
ll euler(ll n) { //log(n)时间内求一个数的欧拉值
    if (vis.count(n))
    {
        return vis[n];
    }
    ll ans = n;
    for (ll i = 2; i * i <= n; i++) {
        if (n % i == 0)
        {
            ans -= ans / i;
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) ans -= ans / n;
    vis[n] = ans;
    return ans;
}

ll solve(int l, int r, ll m)
{
    if (l == r || m == 1)
        return mod(a[r], m);
    return powmod(a[l], solve(l + 1, r, euler(m)), m);
}
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    // gbtb;
    // cin >> n >> m;
    scanf("%d%lld", &n, &m);
    repd(i, 1, n)
    {
        scanf("%lld", &a[i]);
        // cin >> a[i];
    }
    // cin >> q;
    scanf("%d", &q);
    int l, r;
    while (q--)
    {
        scanf("%d %d", &l, &r);
        printf("%lld\n", solve(l, r, m) % m);
        // cin >> l >> r;
        // cout << solve(l, r, m) % m << endl;
    }

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}