AVL树的介绍和实现
一、AVL树
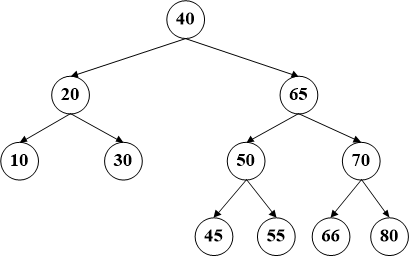
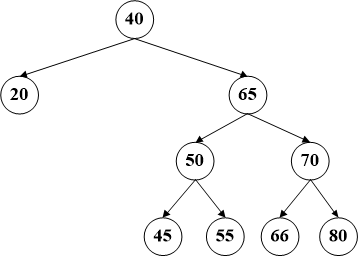
AVL树是一种自平衡二叉查找树,因此在了解AVL树之前先介绍一下平衡二叉树。所谓平衡二叉树即该树中的任一个节点的左子树和右子树高度差不会超过1。如下图左是平衡二叉树,而右图则不是。节点40的左子树高度为1,而右子树高度为3,这样就相差了2,所以不是一个平衡二叉树,平衡树其实并不注重节点的顺序,所以应用更多的一般是平衡二叉查找树。相比于普通的二叉查找树,AVL能够避免由于插入顺序导致子树高度不平衡,甚至退化为链表的情况,能够最大化期望查找效率,使得查找时间复杂度为O(logn)。
二、如何实现平衡
在一个新的节点插入后,不平衡的情况均为以下四种情况之一,分别称其为LL,RR,LR和RL。下面四个图分别代表这四种情况。

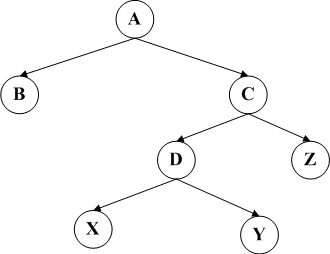
LL和RR旋转的方案分别是

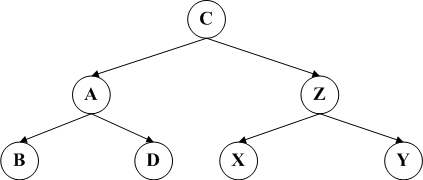
而LR和RL要稍微复杂一些,需要经过两次旋转,前者需要先RR后LL的旋转方案,而后者需要先LL后RR的旋转方案。
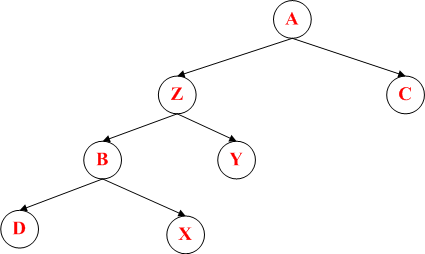
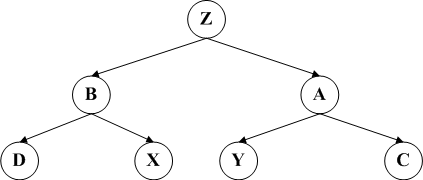

上述红色节点代表是经过一次旋转后的结果,而黑色图代表最终结果。两个分别代表LR和RL的旋转方案。
三、最终的实现
AVL树的介绍和实现的更多相关文章
- AVL树(三)之 Java的实现
概要 前面分别介绍了AVL树"C语言版本"和"C++版本",本章介绍AVL树的Java实现版本,它的算法与C语言和C++版本一样.内容包括:1. AVL树的介绍 ...
- AVL树(一)之 图文解析 和 C语言的实现
概要 本章介绍AVL树.和前面介绍"二叉查找树"的流程一样,本章先对AVL树的理论知识进行简单介绍,然后给出C语言的实现.本篇实现的二叉查找树是C语言版的,后面章节再分别给出C++ ...
- AVL树(二)之 C++的实现
概要 上一章通过C语言实现了AVL树,本章将介绍AVL树的C++版本,算法与C语言版本的一样. 目录 1. AVL树的介绍2. AVL树的C++实现3. AVL树的C++测试程序 转载请注明出处:ht ...
- AVL树(Java实现)
AVL树基本介绍 AVL树是一种自平衡的二叉查找树,在AVL树中任何节点的两个子树的高度差不能超过1.就是相当于在二叉搜索树的基础上,在插入和删除时进行了平衡处理. 不平衡的四种情况 LL:结构介绍 ...
- "《算法导论》之‘树’":AVL树
本文关于AVL树的介绍引自博文AVL树(二)之 C++的实现,与二叉查找树相同的部分则不作介绍直接引用:代码实现是在本文的基础上自己实现且继承自上一篇博文二叉查找树. 1.AVL树的介绍 AVL树是高 ...
- AVL树之 Java的实现
AVL树的介绍 AVL树是高度平衡的而二叉树.它的特点是:AVL树中任何节点的两个子树的高度最大差别为1. 上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1:而右边的不 ...
- AVL树和平衡二叉树 平衡因子 右旋转LL 左旋转RR LR RL
前言 今天要介绍几种高级数据结构AVL树,介绍之前AVL,会先说明平衡二叉树,并将树的学习路线进行总结,并介绍维持平衡的方法:右旋转.左旋转. 一.树学习路线 1.路线总结 总结了一下树的学习路线,如 ...
- 数据结构与算法——AVL树类的C++实现
关于AVL树的简单介绍能够參考:数据结构与算法--AVL树简单介绍 关于二叉搜索树(也称为二叉查找树)能够參考:数据结构与算法--二叉查找树类的C++实现 AVL-tree是一个"加上了额外 ...
- 再回首数据结构—AVL树(二)
前面主要介绍了AVL的基本概念与结构,下面开始详细介绍AVL的实现细节: AVL树实现的关键点 AVL树与二叉搜索树结构类似,但又有些细微的区别,从上面AVL树的介绍我们知道它需要维护其左右节点平衡, ...
随机推荐
- c++文件指针读写图片文件
#include "stdafx.h"#include <string>using namespace std;int _tmain(int argc, _TCHAR* ...
- [官网] 一个很好的 search rpm 或者是deb 包的网站
https://pkgs.org Home About About pkgs.org - Packages Search The pkgs.org is created to provide you ...
- (5.15)mysql高可用系列——MHA实践
关键词:MHA,mysql mha [1]需求 采用mysql技术,实现MHA高可用主从环境,预计未来数据量几百G MHA概念参考:MYSQL高可用技术概述 [2]环境技术架构 [2.1]MHA简介 ...
- Response.write()弹出窗口的问题!
今天偶然发现在.NET中使用Javascript语句弹出窗口时发现一个小小的问题! 例子如下: 1: Response.Write ("<script languge=javascri ...
- Treasure Island(两遍dfs)-- Codeforces Round #583 (Div. 1 + Div. 2, based on Olympiad of Metropolises)
题意:https://codeforc.es/contest/1214/problem/D 给你一个n*m的图,每次可以往右或者往下走,问你使(1,1)不能到(n,m)最少要放多少 ‘ # ’ . 思 ...
- 【二分】Shell Pyramid
[来源]:2008年哈尔滨区域赛 [题目链接]: http://acm.hdu.edu.cn/showproblem.php?pid=2446 [题意] 题目是真的长呀,其实就问一个问题. 按照图里面 ...
- 位运算解决“一个数组中,只有一个数字出现n次,其他数字出现k次”问题
转自:https://blog.csdn.net/monster_girl/article/details/52928864 在学习完位操作后,经常会遇到一类关于查找缺失整数的问题. 第一类是给你一个 ...
- Hello World!!!
C #include <stdio.h> int main() #main 入口函数 { printf("Hello,World!"); #printf 函数打印 ; ...
- windowsformshost mouse event not transmit to it's parent control
in the case you can do it to fix: MouseEventArgs e = new MouseEventArgs(Mouse.PrimaryDevice, 0); e.R ...
- 使用Enablebuffering多次读取Asp Net Core 请求体
使用Enablebuffering多次读取Asp Net Core 请求体 1 .Net Core 2.X时代 使用EnableRewind倒带 public IActionResult Index( ...
