HDU 4498 Function Curve （自适应simpson）

Function Curve

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 203    Accepted Submission(s): 67

Problem Description

Given sequences of k₁, k₂, … k_n, a₁, a₂, …, a_n and b₁, b₂, …, b_n. Consider following function: 

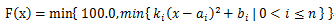
Then we draw F(x) on a xy-plane, the value of x is in the range of [0,100]. Of course, we can get a curve from that plane. 
Can you calculate the length of this curve？

 

Input

The first line of the input contains one integer T (1<=T<=15), representing the number of test cases. 
Then T blocks follow, which describe different test cases. 
The first line of a block contains an integer n ( 1 <= n <= 50 ). 
Then followed by n lines, each line contains three integers k_i, a_i, b_i ( 0<=a_i, b_i<100, 0<k_i<100 ) .

 

Output

For each test case, output a real number L which is rounded to 2 digits after the decimal point, means the length of the curve.

 

Sample Input

2
3
1 2 3
4 5 6
7 8 9
1
4 5 6

 

Sample Output

215.56
278.91

Hint

All test cases are generated randomly.

 

Source

2013 ACM-ICPC吉林通化全国邀请赛——题目重现

 

Recommend

liuyiding

 

数值方法计算积分

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013-10-9 12:04:07
 File Name     :E:\2013ACM\专题学习\数学\积分\HDU4498.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;

 vector<double>x;

 void add(int a1,int b1,int c1)//计算a1*x^2 + b1*x + c = 0的解
 {
     if(a1 ==  && b1 == )
     {
         return;
     }
     if(a1 == )
     {
         double t = -c1*1.0/b1;
         if(t >=  && t <= )
             x.push_back(t);
         return;
     }
     long long deta = b1*b1 - 4LL*a1*c1;
     if(deta < )return;
     if(deta == )
     {
         double t = (-1.0 * b1)/(2.0 * a1);
         if(t >=  && t <= )
             x.push_back(t);
     }
     else
     {
         double t1 = (-1.0 * b1 + sqrt(1.0*deta))/(2.0*a1);
         double t2 = (-1.0 * b1 - sqrt(1.0*deta))/(2.0*a1);
         if(t1 >=  && t1 <= )
             x.push_back(t1);
         if(t2 >=  && t2 <= )
             x.push_back(t2);
     }
 }
 int A[],B[],C[];
 int best;
 double F(double x1)
 {
     return sqrt(1.0 + (x1**A[best] + 1.0 * B[best])*(x1**A[best] + 1.0 * B[best]));
 }
 double simpson(double a,double b)
 {
     double c = a + (b-a)/;
     return (F(a) + *F(c) + F(b))*(b-a)/;
 }
 double asr(double a,double b,double eps,double A)
 {
     double c = a + (b-a)/;
     double L = simpson(a,c);
     double R = simpson(c,b);
     if(fabs(L+R-A) <= *eps)return L+R+(L+R-A)/;
     return asr(a,c,eps/,L) + asr(c,b,eps/,R);
 }
 double asr(double a,double b,double eps)
 {
     return asr(a,b,eps,simpson(a,b));
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int T;
     int k,a,b;
     scanf("%d",&T);
     while(T--)
     {
         int n;
         scanf("%d",&n);
         A[] = ;
         B[] = ;
         C[] = ;
         for(int i = ;i <= n;i++)
         {
             scanf("%d%d%d",&k,&a,&b);
             A[i] = k;
             B[i] = -*a*k;
             C[i] = k*a*a + b;
         }
         x.clear();
         for(int i = ;i <= n;i++)
             for(int j = i+;j <= n;j++)
                 add(A[i]-A[j],B[i] - B[j],C[i] - C[j]);
         double ans = ;
         x.push_back();
         x.push_back();
         sort(x.begin(),x.end());
         int sz = x.size();
         for(int i = ;i < sz-;i++)
         {
             double x1 = x[i];
             double x2 = x[i+];
             if(fabs(x2-x1) < 1e-)continue;
             double mid = (x1 + x2)/;
             best = ;
             for(int j = ;j <= n;j++)
             {
                 double tmp1 = mid*mid*A[best] + mid*B[best] + C[best];
                 double tmp2 = mid*mid*A[j] + mid*B[j] + C[j];
                 if(tmp2 < tmp1)best = j;
             }
             ans += asr(x1,x2,1e-);
         }
         printf("%.2lf\n",ans);
     }
     return ;
 }