统计学习方法ｃ++实现之六 支持向量机（SVM）及SMO算法

前言

支持向量机（SVM）是一种很重要的机器学习分类算法，本身是一种线性分类算法，但是由于加入了核技巧，使得SVM也可以进行非线性数据的分类；SVM本来是一种二分类分类器，但是可以扩展到多分类，本篇不会进行对其推导一步一步罗列公式，因为当你真正照着书籍进行推导后你就会发现他其实没那么难，主要是动手。本篇主要集中与实现，即使用著名的序列最小最优化（SMO）算法进行求解，本篇实现的代码主要参考了Platt J. Sequential minimal optimization: A fast algorithm for training support vector machines[J]. 1998.这是SMO的论文，论文中详细解释了如何使用SMO算法，还有伪代码，我的C++程序就是根据伪代码实现的（没错，SMO算法我推不出来）。代码地址.

对于SVM的一些理解

首先，《统计学习方法》中对于SVM的讲解已经很好了，请务必跟着一步一步推导，这样你就会发现整个SVM的推导过程无非就是以下几步：

1. 将分类器建模成n维空间中的超平面，但是这个超平面有个很重要的选取原则，那就是让所有样本点到超平面的距离都尽量大，也就是让距离超平面最近的点到超平面的距离达到最大，于是得出了约束最大化问题。
2. 将问题简化到只和决定超平面的参数w有关，使用熟悉的拉格朗日数乘法将约束最优化问题变成一个式子，然后转化为对偶问题。
3. 求解对偶问题的最优解a，然后根据原问题和对偶问题的关系由a求出w，此时就得到SVM的参数了。

1,2步都是需要推导的，唯独涉及实现的地方是第3步，我们实现的重点变成了如何快速的得到最优解a（a可是有N个分量的，N为训练样本数）。于是SMO算法就出现了。

再者关于核函数，之前看博客，有人理解成核函数是一种映射，即将非线性问题映射为线性问题，有人评论说这是不严谨的，核函数不是一种映射，当时很迷茫，但是现在看来，核函数是一种技巧，他让我们可以使用目前空间的内积来代表某个目标空间的内积。

具体的关于SVM的推导和核技巧的理解查看书籍就可以，自己推导一遍就都明白了。

序列最小最优化（SMO）算法

《统计学习方法》上对于SMO算法的讲解很清楚（跟原论文思路一样），就是将待优化的n个参数选两个作为优化对象，其他的固定，然后转化为二元最优化问题。道理我都懂，但是实现的时候遇到了很多麻烦，关键在于启发式的变量选取，于是便找到原论文，没想到Platt大神已经把伪代码写好了，于是，我就把他的伪代码用c++实现了一遍。这部分我对一些推导还是不明白，在这里就不献丑了，看代码吧，首先给出论文中的伪代码截图。

代码结构

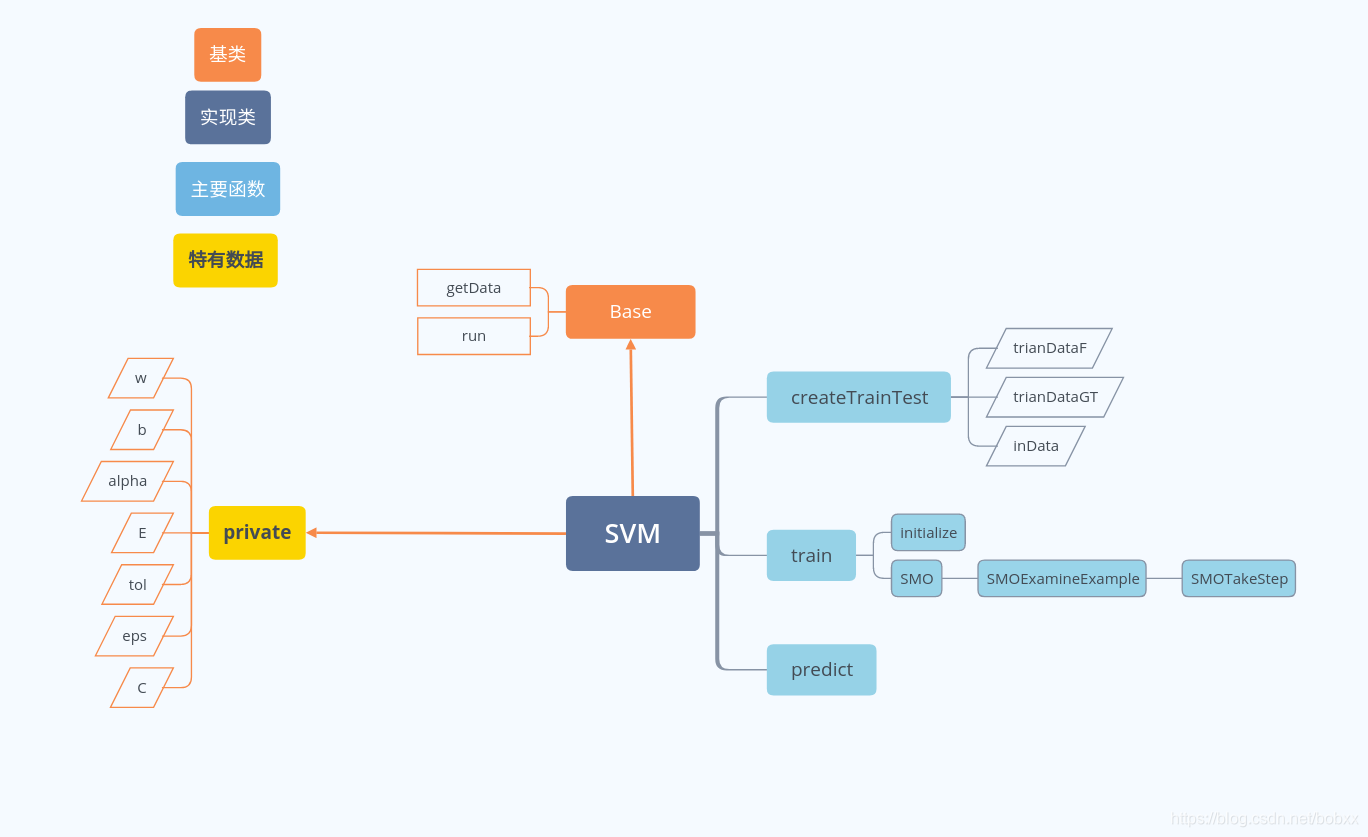
c++实现

这部分主要列出伪代码的takestep部分各变量的更新代码。

int SVM::SMOTakeStep(int& i1, int& i2) {
    //变量名跟伪代码中基本一样，这里用i1， i2代表数据点对应的的拉格朗日乘子，E每个样本点的预测输出与真值的误差
    //存储在vector中，避免重复计算
    ...
    ...
    ...
    double a1 = alpha[i1] + s * (alpha[i2] - a2);
    double b1;
    //please notice that the update equation is from <<统计学习方法>>p130, not the equation in paper
    b1= -E[i1] - y1 * (a1 - alpha[i1]) * kernel(trainDataF[i1], trainDataF[i1]) -
                y2 * (a2 - alpha[i2]) * kernel(trainDataF[i1], trainDataF[i2]) + b;
    double b2;
    b2 = -E[i2] - y1 * (a1 - alpha[i1]) * kernel(trainDataF[i1], trainDataF[i2]) -
                y2 * (a2 - alpha[i2]) * kernel(trainDataF[i2], trainDataF[i2]) + b;
    double bNew = (b1 + b2) / 2;
    b = bNew;
    w = w + y1 * (a1 - alpha[i1]) * trainDataF[i1] + y2 * (a2 - alpha[i2]) *
                                                     trainDataF[i2];
    //this is the linear SVM case, this equation are from the paper equation 22
    alpha[i1] = a1;
    alpha[i2] = a2;
//    vector<double> wtmp (indim);
//    for (int i=0; i<trainDataF.size();++i)
//    {
//        auto tmp = alpha[i]*trainDataF[i]*trainDataGT[i];
//        wtmp = wtmp+tmp;
//    }
//    w = wtmp;
    E[i1] = computeE(i1);
    E[i2] = computeE(i2);
    return 1;

特别注意b的计算公式，这里被坑了好久，原论文的计算b1 ,b2的公式全是正号，因为论文中svm的超平面公式是\(wx-b\),这与书上的公式不同，所以导致我的算法一直不收敛，最后从头看论文才发现...

其他的实现都在这里，如果有问题欢迎交流。