PCA和白化练习之处理二维数据

在很多情况下，我们要处理的数据的维度很高，需要提取主要的特征进行分析这就是PCA（主成分分析），白化是为了减少各个特征之间的冗余，因为在许多自然数据中，各个特征之间往往存在着一种关联，为了减少特征之间的关联，需要用到所谓的白化（whitening）.

首先下载数据pcaData.rar，下面要对这里面包含的45个2维样本点进行PAC和白化处理，数据中每一列代表一个样本点。

第一步 画出原始数据：

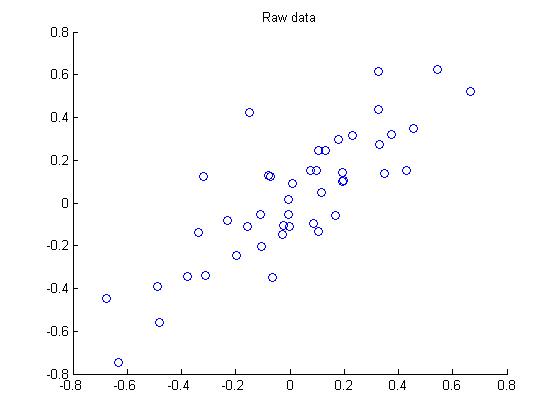
第二步：执行PCA，找到数据变化最大的方向：

第三步：将原始数据投射到上面找的两个方向上：

第四步：降维，此例中把数据由2维降维到1维，画出降维后的数据：

第五步：PCA白化处理：

第六步：ZCA白化处理：

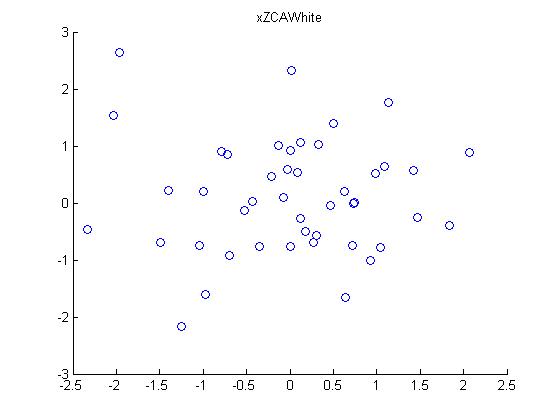
下面是程序matlab源代码：

 close all;clear all;clc;

 %%================================================================
 %% Step : Load data
 %  We have provided the code to load data from pcaData.txt into x.
 %  x is a  *  matrix, where the kth column x(:,k) corresponds to
 %  the kth data point.Here we provide the code to load natural image data into x.
 %  You do not need to change the code below.

 x = load('pcaData.txt','-ascii');
 figure();
 scatter(x(, :), x(, :));
 title('Raw data');

 %%================================================================
 %% Step 1a: Implement PCA to obtain U
 %  Implement PCA to obtain the rotation matrix U, which is the eigenbasis
 %  sigma. 

 % -------------------- YOUR CODE HERE --------------------
 u = zeros(size(x, )); % You need to compute this

 sigma = x * x'/ size(x, 2);
 [u,S,V] = svd(sigma);

 % --------------------------------------------------------
 hold on
 plot([ u(,)], [ u(,)]);
 plot([ u(,)], [ u(,)]);
 scatter(x(, :), x(, :));
 hold off

 %%================================================================
 %% Step 1b: Compute xRot, the projection on to the eigenbasis
 %  Now, compute xRot by projecting the data on to the basis defined
 %  by U. Visualize the points by performing a scatter plot.

 % -------------------- YOUR CODE HERE --------------------
 xRot = zeros(size(x)); % You need to compute this
 xRot = u' * x;

 % -------------------------------------------------------- 

 % Visualise the covariance matrix. You should see a line across the
 % diagonal against a blue background.
 figure();
 scatter(xRot(, :), xRot(, :));
 title('xRot');

 %%================================================================
 %% Step : Reduce the number of dimensions from  to .
 %  Compute xRot again (this time projecting to  dimension).
 %  Then, compute xHat by projecting the xRot back onto the original axes
 %  to see the effect of dimension reduction

 % -------------------- YOUR CODE HERE --------------------
 k = ; % Use k =  and project the data onto the first eigenbasis
 xHat = zeros(size(x)); % You need to compute this
 z = u(:, :k)' * x;
 xHat = u(:,:k) * z;

 % --------------------------------------------------------
 figure();
 scatter(xHat(, :), xHat(, :));
 title('xHat');

 %%================================================================
 %% Step : PCA Whitening
 %  Complute xPCAWhite and plot the results.

 epsilon = 1e-;
 % -------------------- YOUR CODE HERE --------------------
 xPCAWhite = zeros(size(x)); % You need to compute this

 xPCAWhite = diag( ./ sqrt(diag(S) + epsilon)) * xRot;

 % --------------------------------------------------------
 figure();
 scatter(xPCAWhite(, :), xPCAWhite(, :));
 title('xPCAWhite');

 %%================================================================
 %% Step : ZCA Whitening
 %  Complute xZCAWhite and plot the results.

 % -------------------- YOUR CODE HERE --------------------
 xZCAWhite = zeros(size(x)); % You need to compute this

 xZCAWhite = u * xPCAWhite;
 % --------------------------------------------------------
 figure();
 scatter(xZCAWhite(, :), xZCAWhite(, :));
 title('xZCAWhite');

 %% Congratulations! When you have reached this point, you are done!
 %  You can now move onto the next PCA exercise. :)