Programming Assignment 3: Pattern Recognition

编程作业三

作业链接：Pattern Recognition & Checklist

我的代码：BruteCollinearPoints.java & FastCollinearPoints.java & Point.java

问题简介

计算机视觉涉及分析视觉图像中的模式并重建产生它们的现实世界对象。该过程通常分为两个阶段：特征检测和模式识别。特征检测涉及选择图像的重要特征；模式识别涉及发现特征中的模式。我们将研究一个涉及点和线段的特别简单的模式识别问题。这种模式识别出现在许多其他应用中，例如统计数据分析。

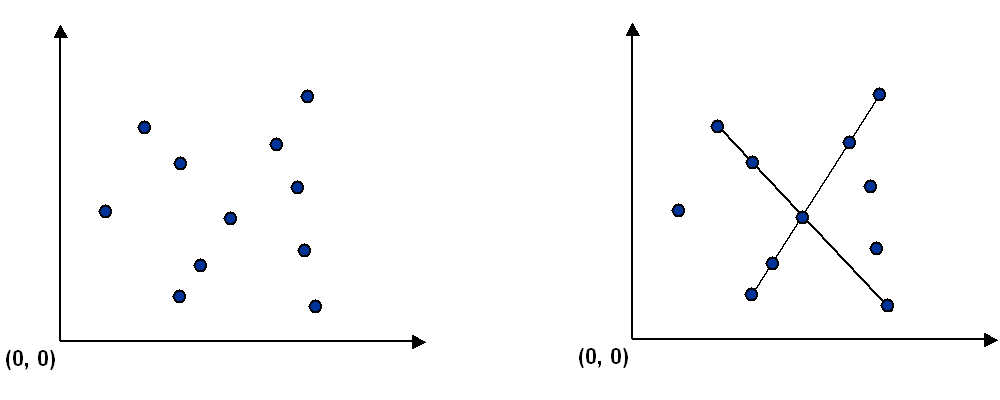
The problem. Given a set of n distinct points in the plane, find every(maximal) line segment that connects a subset of 4 or more of the points.

给定一些点，要求找到所有至少包含四个点的线段。

任务摘要

Point data type. Create an immutable data type Point that represents a point in the plane by implementing the following API:

public class Point implements Comparable<Point> {
  public Point(int x, int y)                         // constructs the point (x, y)

  public   void draw()                               // draws this point
  public   void drawTo(Point that)                   // draws the line segment from this point to that point
  public String toString()                           // string representation

  public               int compareTo(Point that)     // compare two points by y-coordinates, breaking ties by x-coordinates
  public            double slopeTo(Point that)       // the slope between this point and that point
  public Comparator<Point> slopeOrder()              // compare two points by slopes they make with this point
}

实现表示点的数据类型，要求完成后三个方法，详细参见：specification。

Brute force. Write a program BruteCollinearPoints.java that examines 4 points at a time and checks whether they all lie on the same line segment, returning all such line segments. To check whether the 4 points p, q, r, and s are collinear, check whether the three slopes between p and q, between p and r, and between p and s are all equal.

public class BruteCollinearPoints {
public BruteCollinearPoints(Point[] points)    // finds all line segments containing 4 points
public           int numberOfSegments()        // the number of line segments
public LineSegment[] segments()                // the line segments
}

除了暴力检测每四个点是否共线（\(n^{4}\)），还有更快的做法，对点 P：

• 把 P 当做原点。

• 其它点按和点 P 的斜率（slope）排序。

• 检查是否有三个点（或者更多）有同样的斜率。如果有，那这些点和点 P 就构成目标线段。

对其它的点，重复上述过程，就能找到所有目标线段，因为排序把斜率一样的点聚在一起。而这算法更快是因为瓶颈操作是排序，排序是 nlgn，最后是 \(n^{2}lgn\)，也比 \(n^{4}\) 好得多。

Write a program FastCollinearPoints.java that implements this algorithm.

public class FastCollinearPoints {
public FastCollinearPoints(Point[] points)     // finds all line segments containing 4 or more points
public           int numberOfSegments()        // the number of line segments
public LineSegment[] segments()                // the line segments
}

问题分析

仍然按照 Checklist 里建议的编程步骤，先实现 Point.java。下载 Point.java，完成要求实现的方法。实际上，specification 里说得挺详细的，没什么问题，大概主要是让我们熟悉下可比较接口和比较器。

• The compareTo() method should compare points by their y-coordinates, breaking ties by their x-coordinates. Formally, the invoking point (x0, y0) is less than the argument point (x1, y1) if and only if either y0 < y1 or if y0 = y1 and x0 < x1.

• The slopeTo() method should return the slope between the invoking point (x0, y0) and the argument point (x1, y1), which is given by the formula (y1 − y0) / (x1 − x0). Treat the slope of a horizontal line segment as positive zero; treat the slope of a vertical line segment as positive infinity; treat the slope of a degenerate line segment (between a point and itself) as negative infinity.

• The slopeOrder() method should return a comparator that compares its two argument points by the slopes they make with the invoking point (x0, y0). Formally, the point (x1, y1) is less than the point (x2, y2) if and only if the slope (y1 − y0) / (x1 − x0) is less than the slope (y2 − y0) / (x2 − x0). Treat horizontal, vertical, and degenerate line segments as in the slopeTo() method.

• Do not override the equals() or hashCode() methods.

slopeTo() 方法两个点连线水平时返回正零，Checklist 里也有解释。

What does it mean for slopeTo() to return positive zero?

Java (and the IEEE 754 floating-point standard) define two representations of zero: negative zero and positive zero.

double a = 1.0;
double x = (a - a) /  a;   // positive zero ( 0.0)
double y = (a - a) / -a;   // negative zero (-0.0)

Note that while (x == y) is guaranteed to be true, Arrays.sort() treats negative zero as strictly less than positive zero. Thus, to make the specification precise, we require you to return positive zero for horizontal line segments. Unless your program casts to the wrapper type Double (either explicitly or via autoboxing), you probably will not notice any difference in behavior; but, if your program does cast to the wrapper type and fails only on (some) horizontal line segments, this may be the cause.

接着实现 BruteCollinearPoints.java ，逻辑比较简单，还给了很多提示，也没问题。

To form a line segment, you need to know its endpoints. One approach is to form a line segment only if the 4 points are in ascending order (say, relative to the natural order), in which case, the endpoints are the first and last points.

Hint: don't waste time micro-optimizing the brute-force solution. Though, there are two easy opportunities. First, you can iterate through all combinations of 4 points (N choose 4) instead of all 4 tuples (N^4), saving a factor of 4! = 24. Second, you don't need to consider whether 4 points are collinear if you already know that the first 3 are not collinear; this can save you a factor of N on typical inputs.

把点排下序，线段的起始点自然就是遍历的头尾，甚至也教我们怎么排序。

How do I sort a subarray in Java?

Arrays.sort(a, lo, hi) sorts the subarray from a[lo] to a[hi-1] according to the natural order of a[]. You can use a Comparator as the fourth argument to sort according to an alternate order.

于是，最后的 FastCollinearPoints.java 相对复杂些。我是用了两个排序，一开始和暴力算法一样先按自然顺序排，就是先比 y 再比 x 那种，另一个是遍历点的时候按和该点的斜率排。斜率一样计数的就 ++，不小于三个再看这点的自然顺序是不是最小，是最小才将其和自然顺序最大的组成线段存起来。通过这种方法，获得线段的起始点，避免重复加入线段。

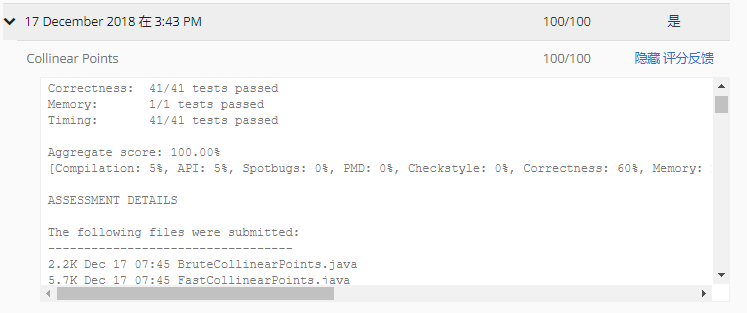
测试结果