【xsy1281】 珠串 打表+乱搞or数位dp

题目大意：你要找出一个有$k$个的本质不同的$n$位二进制数的集合，使得集合中最大的数最小，请输出这个数

本质不同定义：对于一个数$k$，$rev(k)$，$~k$，$rev(~k)$与$k$本质相同。其中$~k$表示对$k$的每一位二进制翻转，$rev(k)$表示对$k$左右翻转。

举个例子：对于数0001，它与1000,1110,0111本质相同。

数据范围：$n≤25,k≤10^{16}$。

此题貌似正解是数位dp，然而我比较菜。

看到这一题：打表啊！

于是打了个表，发现：

若$k≤2^{\lceil \frac{n}{2} \rceil}-2$，则直接输出$k$就可以了，证明显然。

若$k>2^{\lceil \frac{n}{2} \rceil}-2$

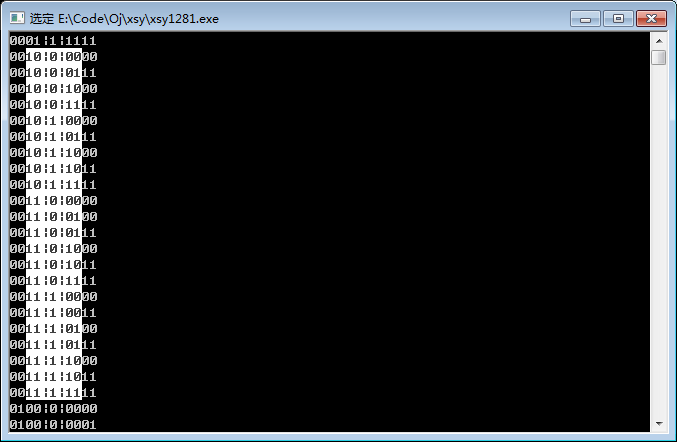
先考虑$n$为偶数的情况，我们打一个表，打出所有满足$rev(x)<x$或$(~x)<x$或$rev(~x)<x$的数，大概长这样

我们发现：以中间的分界线为界，当左侧构成的数去掉前导零后构成$x$，那么以$x$开头的不符合要求的二进制数就有$2x$个。

（感兴趣的同学可以证明一下，我懒得证了23333）

我们基于这一个特征，先确定这个二进制数的前$\frac{n}{2}$位。

后面的$\frac{n}{2}$位直接暴力枚举然后再随便判断一下就好了。

n为奇数的情况相似

以中间为分界线，当右侧横线左侧的数为$x$时，以$x$为前缀的$n$位二进制数有$x$个。

和之前的搞法一样随便搞一搞就可以了。

时间复杂度：$O(2^{n/2})$，空间复杂度：$O(2^{n/2})$。

 #include<bits/stdc++.h>
 #define L long long
 using namespace std;

 int rev[<<]={};
 L n,k;

 void out(L k1){for(L i=;i<n;i++) printf("%d",bool((1LL<<(n-i-))&k1));}

 void SolveEven(){
     L n2=n/,s=<<n2,all=1LL<<n;
     if(k<s){
         out(k);
         return;
     }else k-=s;
     for(int i=;i<s;i++) rev[i]=(rev[i>>]>>)|((i&)?(s>>):);
     for(int i=,j=;i<s;i++,j+=){
         if(k>=s-j) k-=s-j;
         else{
             int p; for(p=;p<s&&k>=;p++){
                 L k1=(1LL*i)<<n2|p;
                 L k2=(1LL*rev[p])<<n2|rev[i];
                 L k3=(1LL*rev[(s--p)&(s-)])<<n2|rev[s--i];
                 if(k2>=k1&&k3>=k1)
                 k--;
             }
             L k1=(1LL*i)<<n2|(p-);
             out(k1);
             return;
         }
     }
     cout<<-<<endl;
 }
 void SolveOdd(){
     L n2=n/,s=<<n2,all=1LL<<n;
     L N2=(n+)/,S=<<N2;
     if(k<S-){
         out(k);
         return;
     }else k-=S-;
     for(int i=;i<s;i++) rev[i]=(rev[i>>]>>)|((i&)?(s>>):);
     for(int i=,j=;i<s;i++,j++){
         if(k>=s-j) k-=s-j;
         else{
             int p; for(p=;p<s&&k>=;p++){
                 L k1=(1LL*i)<<n2|p;
                 L k2=((i&)<<n2)|((1LL*rev[p])<<N2)|rev[i>>];
                 L k3=(((i&)==)<<n2)|((1LL*rev[(s-p-)&(s-)])<<N2)|rev[s--(i>>)];
                 if(k2>=k1&&k3>=k1)
                 k--;
             }
             L k1=(1LL*i)<<n2|(p-);
             out(k1);
             return;
         }
     }
     cout<<-<<endl;
 }

 int main(){
     cin>>n>>k;
     if(n&) SolveOdd();
     else SolveEven();
 }