关于红黑树，在HashMap中是怎么应用的？

关于红黑树，在HashMap中是怎么应用的？

前言

在阅读HashMap源码时，会发现在HashMap中使用了红黑树，所以需要先了解什么是红黑树，以及其原理。从而再进一步阅读HashMap中的链表到红黑树的转换，红黑树的增删节点等。

1. 什么是红黑树？
2. 在HashMap中是怎么应用的？

什么是红黑树？

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它在1972年由鲁道夫·贝尔发明，被称为"对称二叉B树"，它现代的名字源于Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在O(logN)时间内完成查找、插入和删除，这里的n是树中元素的数目。

红黑树的性质

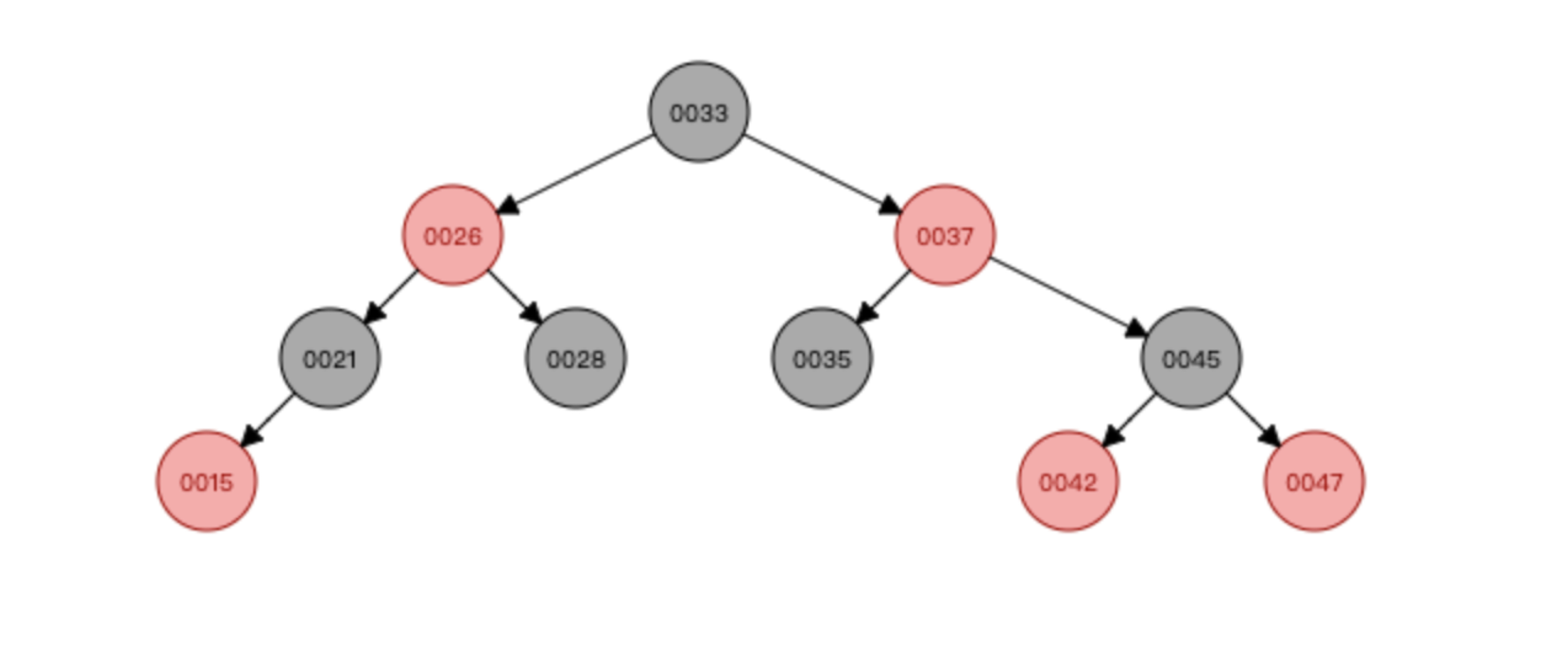
红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是NIL节点）。
4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

红黑树操作

左旋、右旋

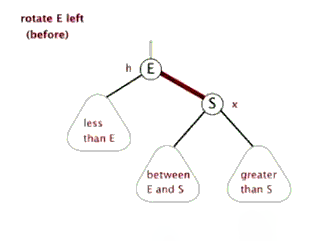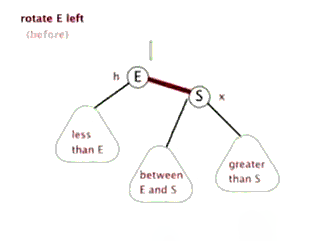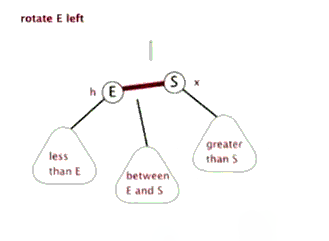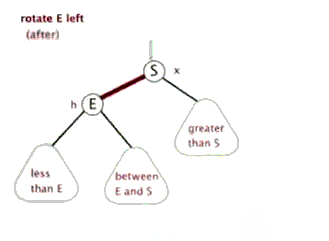
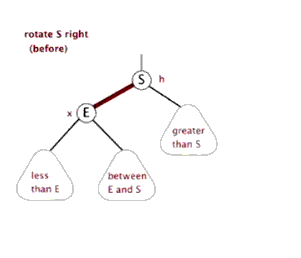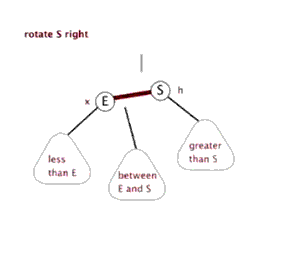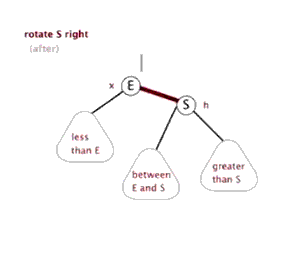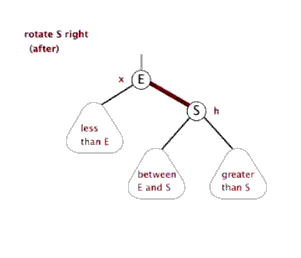
插入

1. 以二叉查找树的方法增加节点
2. 新插入节点为红色（如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑节点，这个是很难调整的。但是设为红色节点后，可能会导致出现两个连续红色节点的冲突，那么可以通过颜色调换（color flips）和树旋转来调整。）

注意：

1. 性质1和性质3是永远保持着的。
2. 性质4只在增加红色节点、重绘黑色节点为红色，或做旋转时受到威胁。
3. 性质5只在增加黑色节点、重绘红色节点为黑色，或做旋转时受到威胁。

插入时会遇到以下五种情形：

情形1：插入第一个节点

情形2：插入新节点，父节点是黑色

情形3：插入新节点，父节点是红色，叔父节点是红色

情形4：插入新节点，父节点是红色，叔父节点是黑色或缺省，新节点是右子节点，父节点又是其父节点的左子节点

情形5：插入新节点，父节点是红色，叔父节点是黑色或缺省，新节点是左子节点，父节点又是其父节点的左子节点。

• 情形1：

操作：插入第一个节点

违反性质2：" 根是黑色。 "

情形：直接插入红色节点，然后进行染色为黑色

• 情形2：

操作：插入新节点，父节点是黑色

未违反性质

情形：直接插入

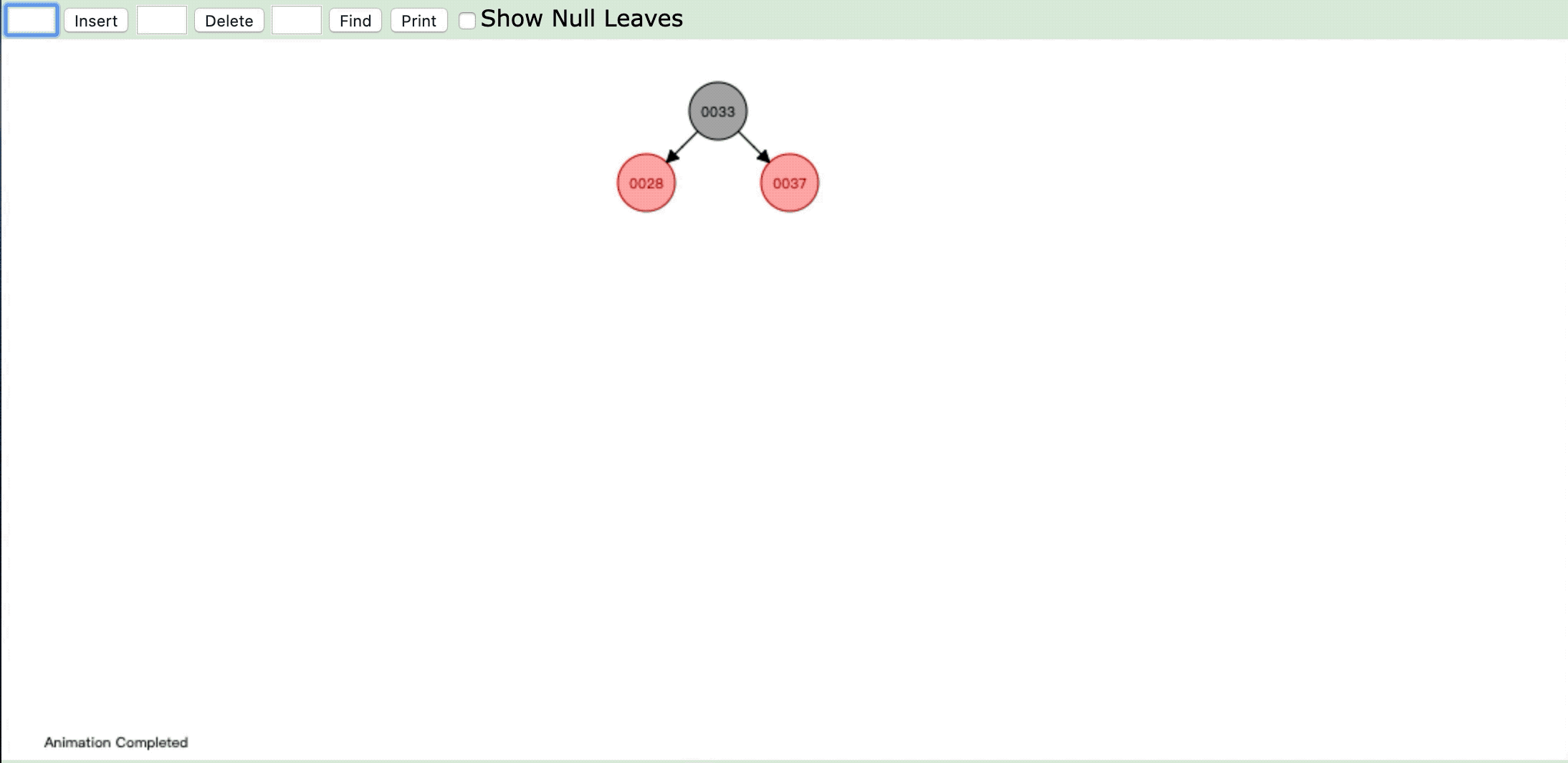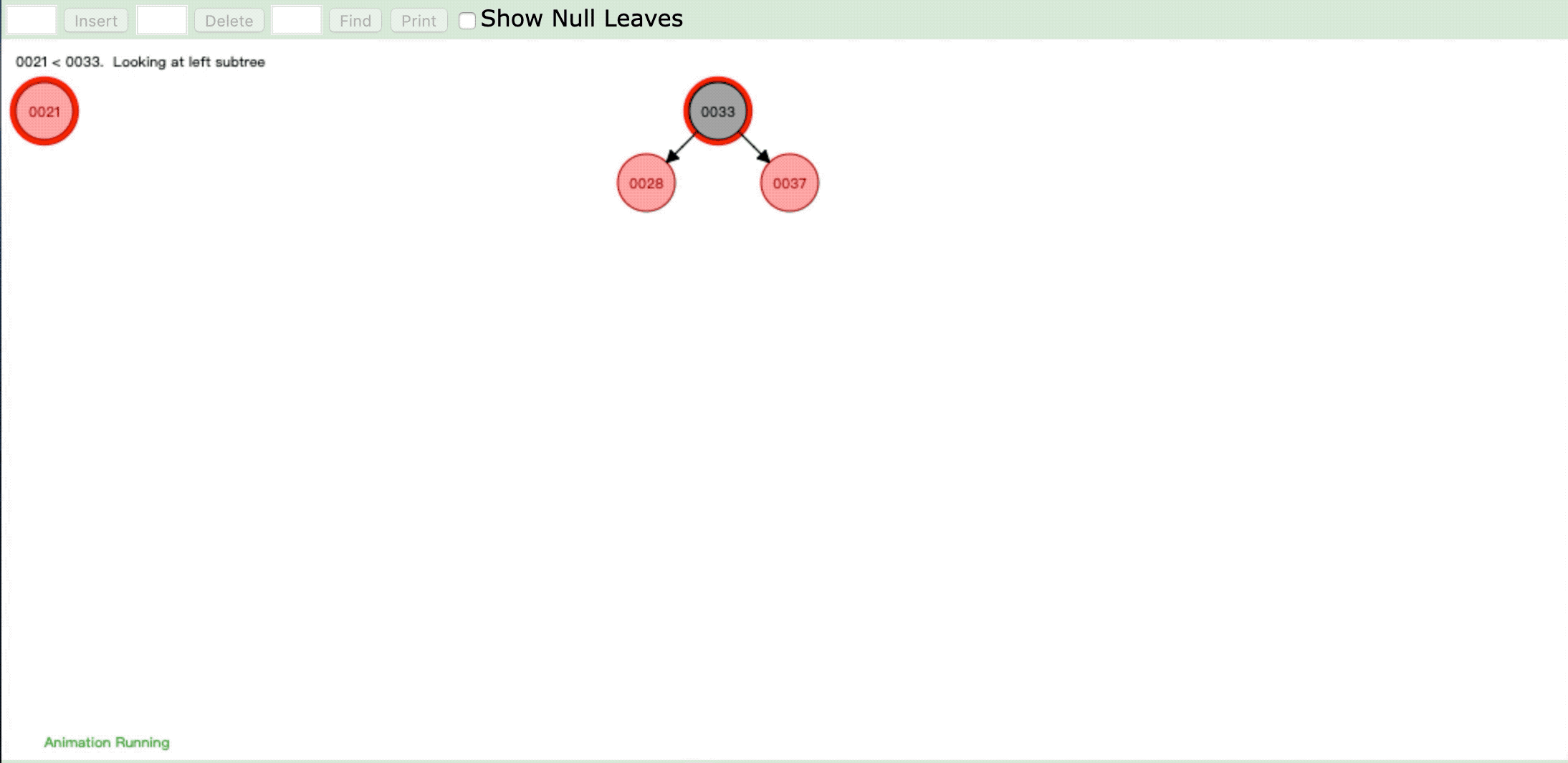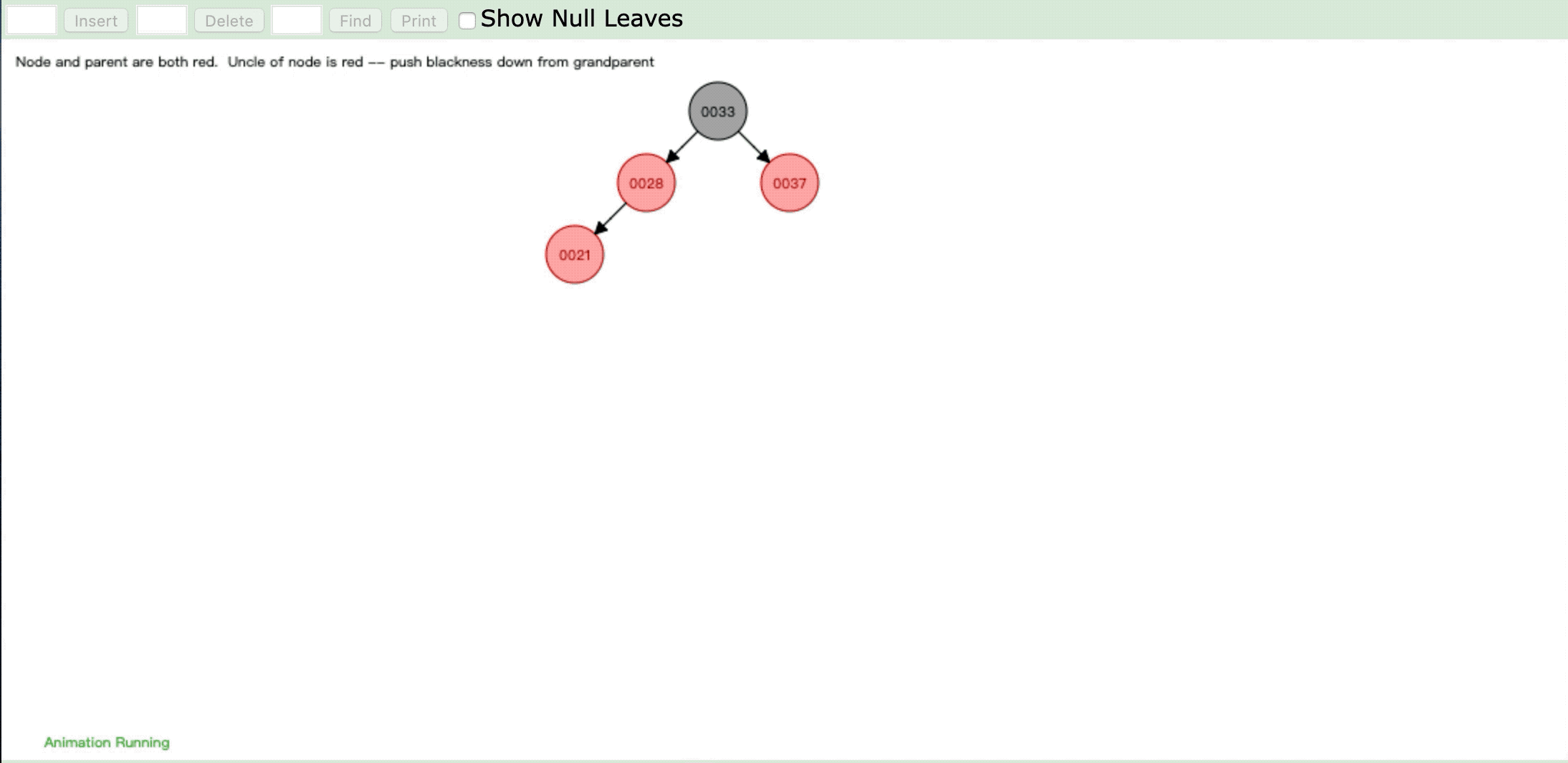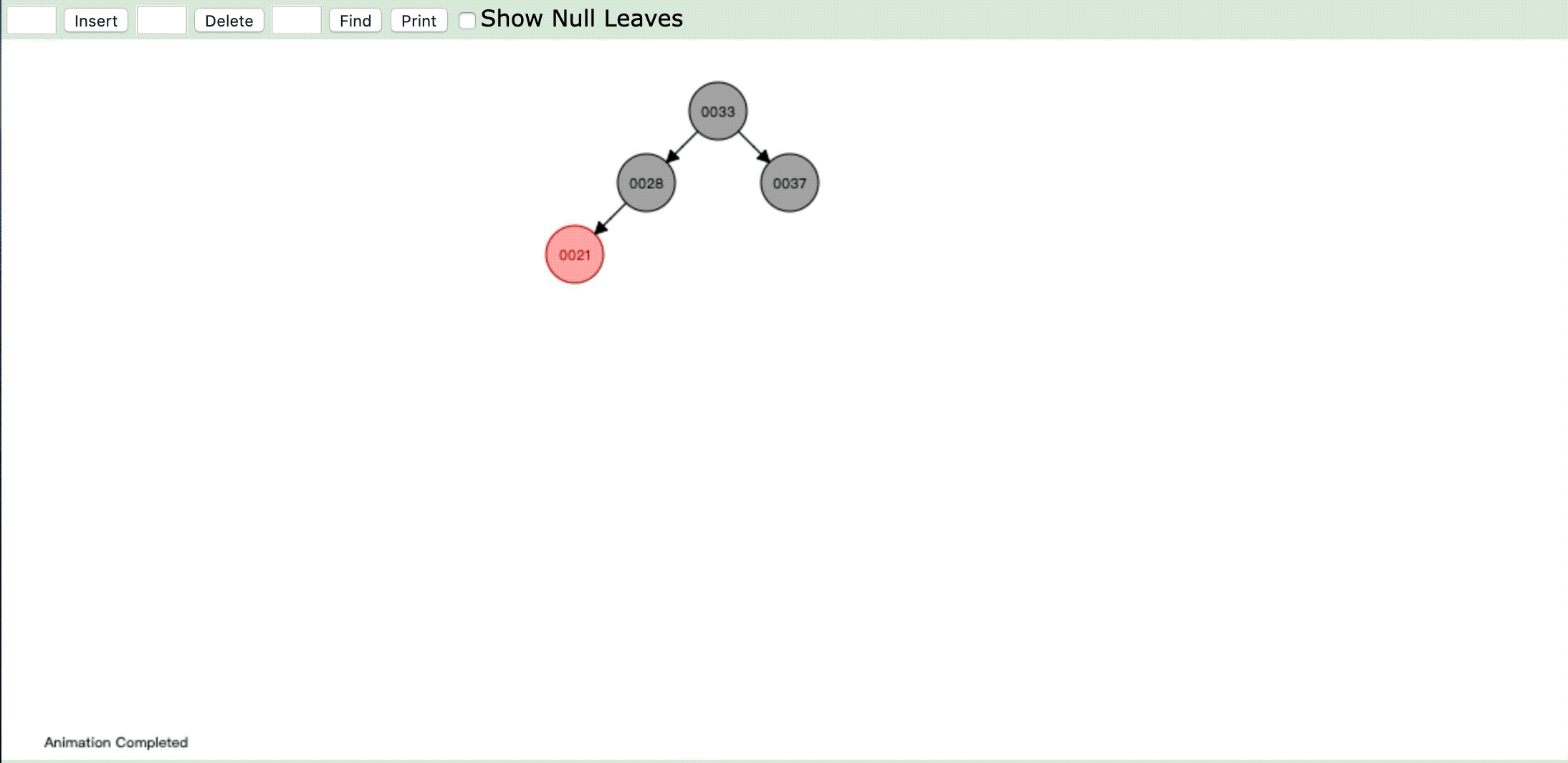
• 情形3：

操作：插入新节点，父节点是红色，叔父节点是红色

违反性质4：" 每个红色节点必须有两个黑色的子节点。 "

情形：将祖父节点染色，祖父节点染色后再进行重新判断进行染色或旋转

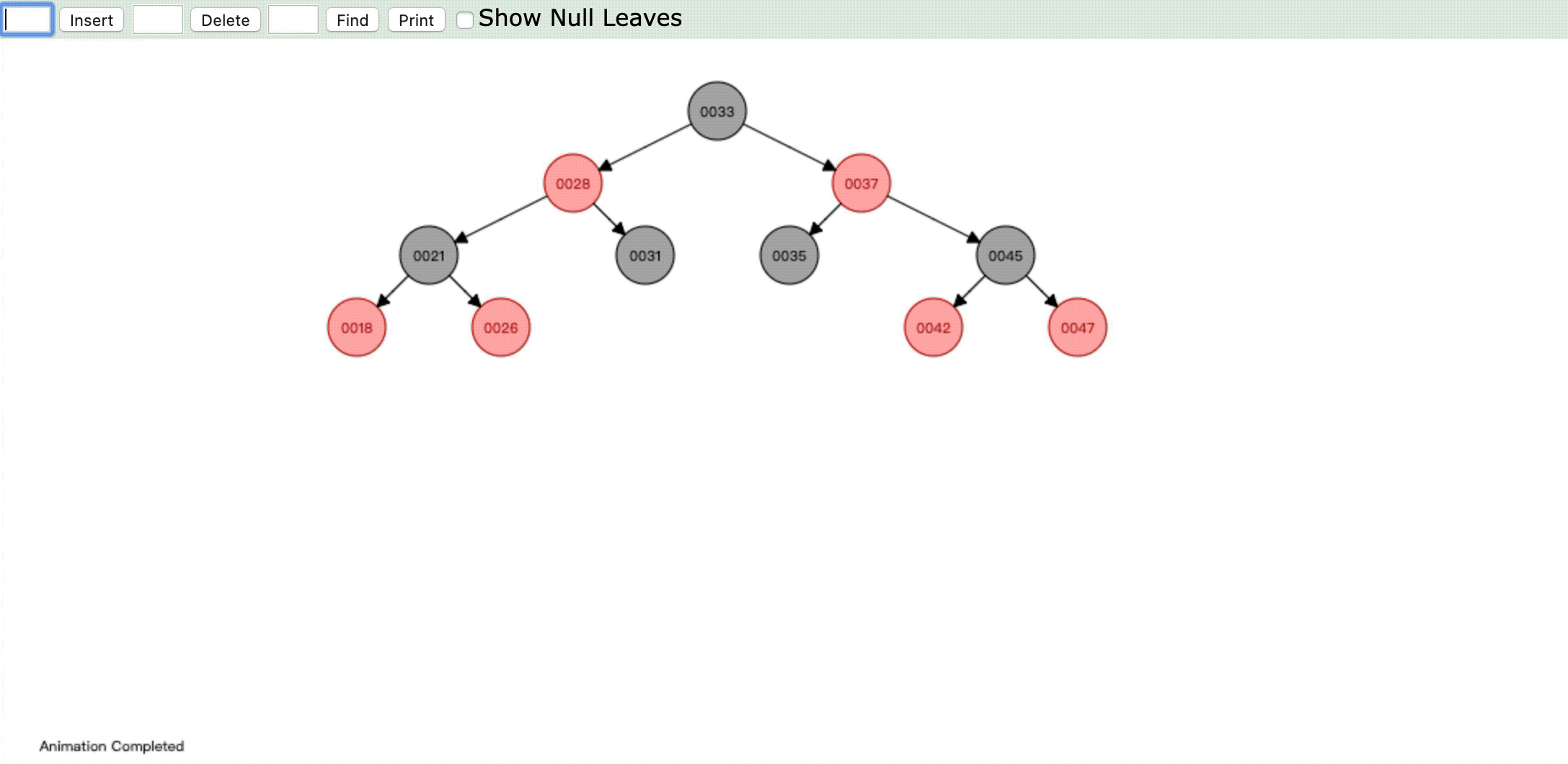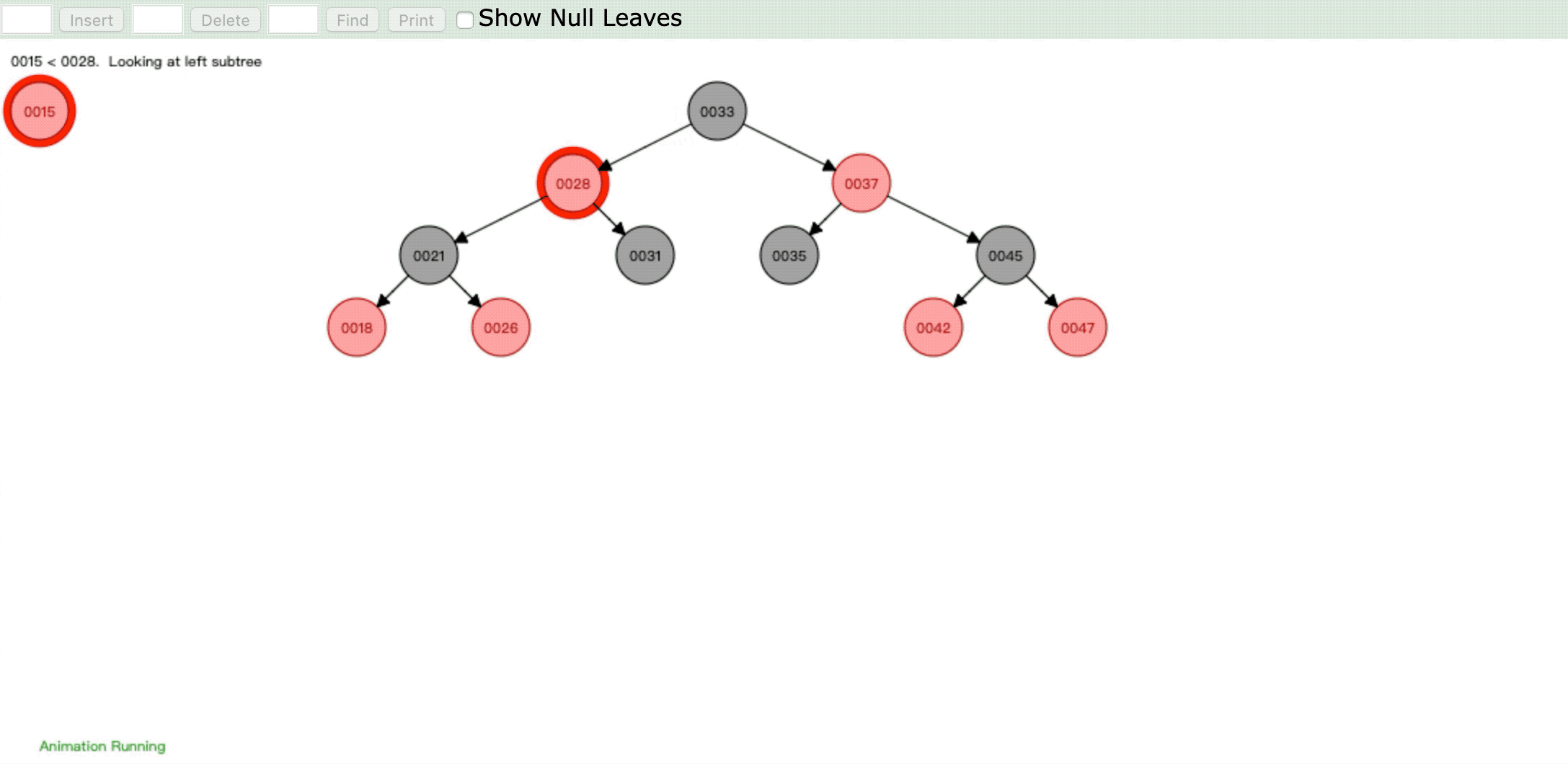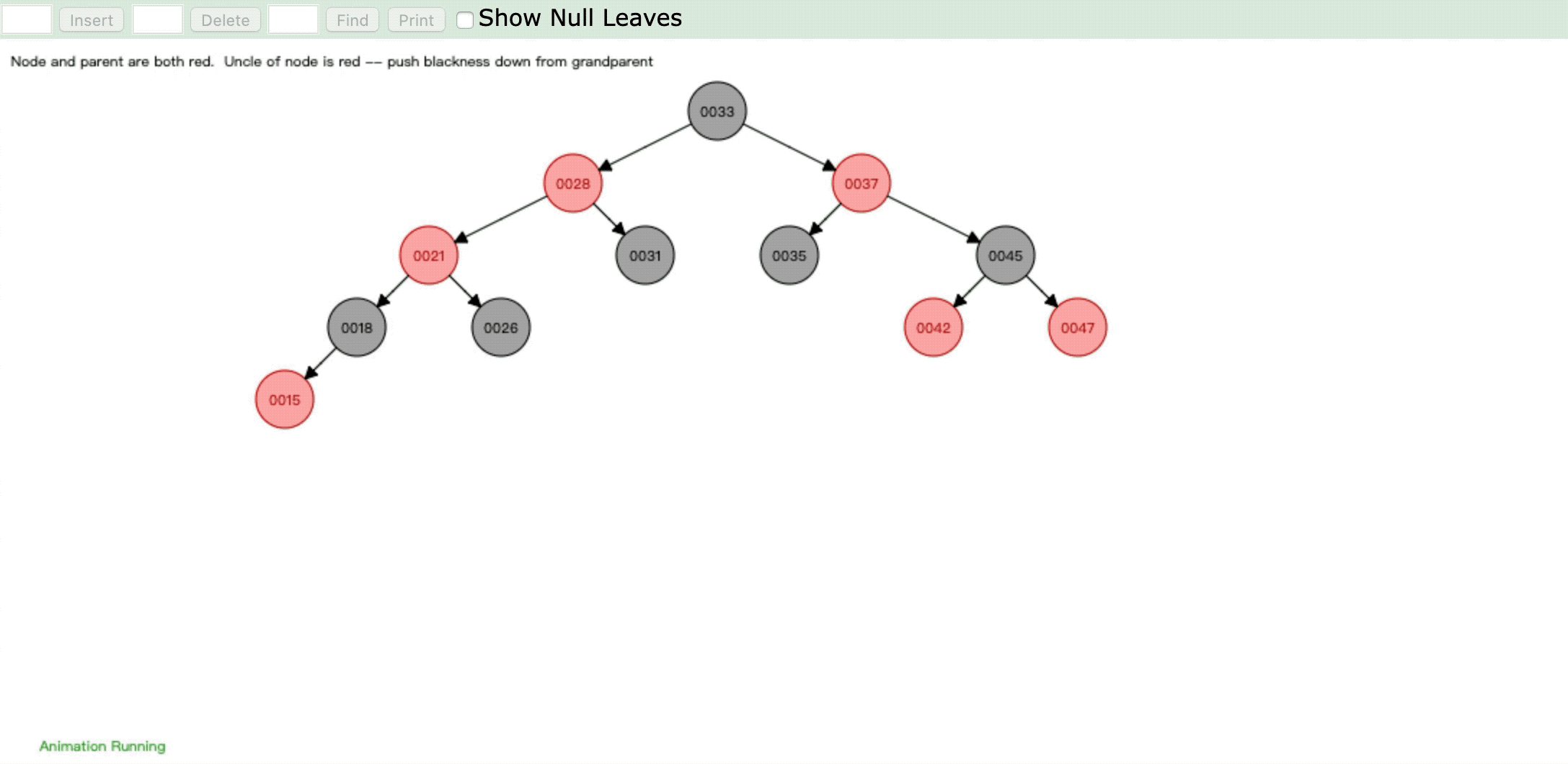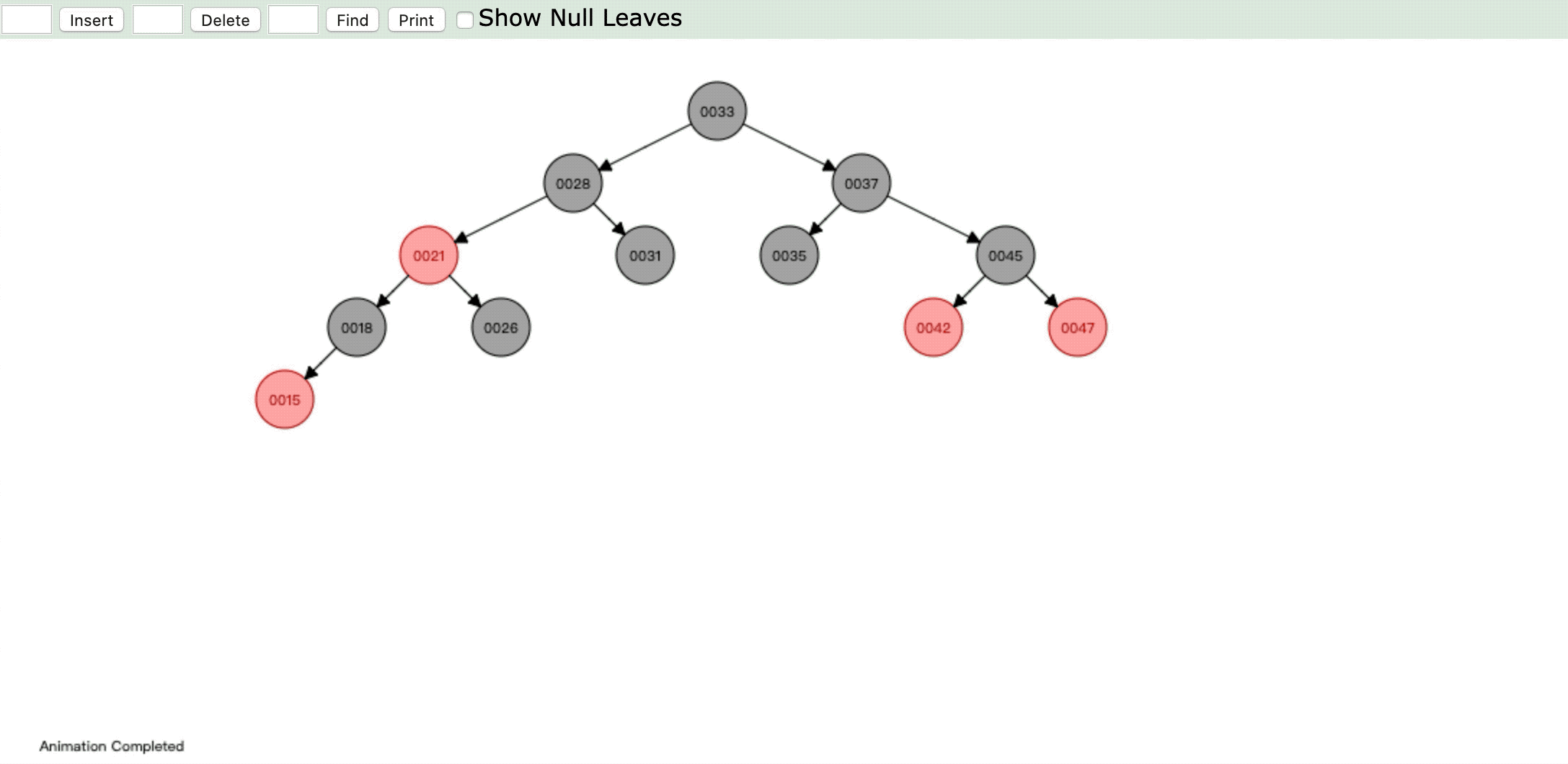
• 情形4：

操作：插入新节点，父节点是红色，叔父节点是黑色或缺省，新节点是右子节点，父节点又是其父节点的左子节点

违反性质4：" 每个红色节点必须有两个黑色的子节点。 "

情形：进行左旋，旋转后父节点变成左子节点，新节点变成父节点，然后重新判断进行染色或旋转

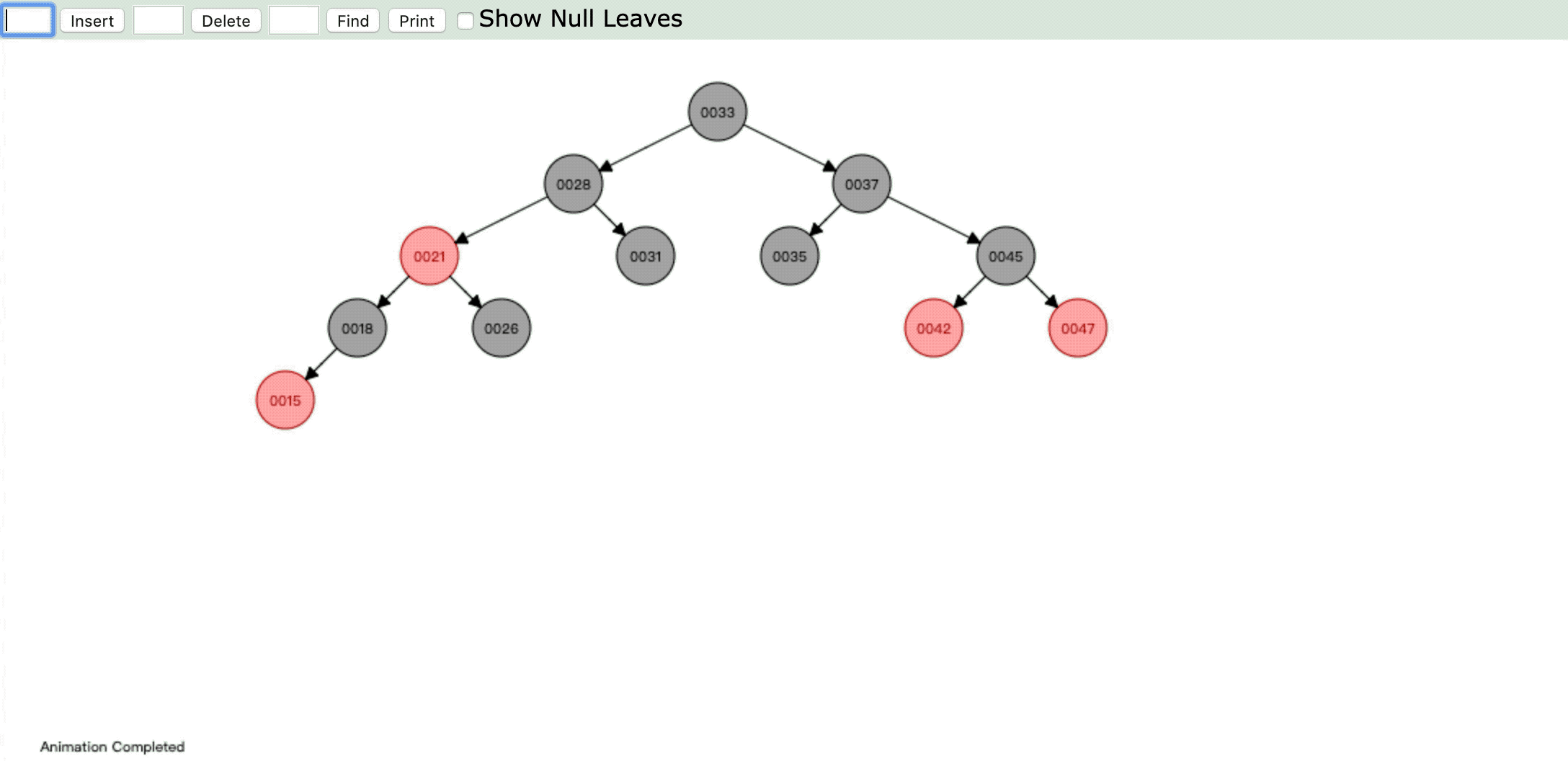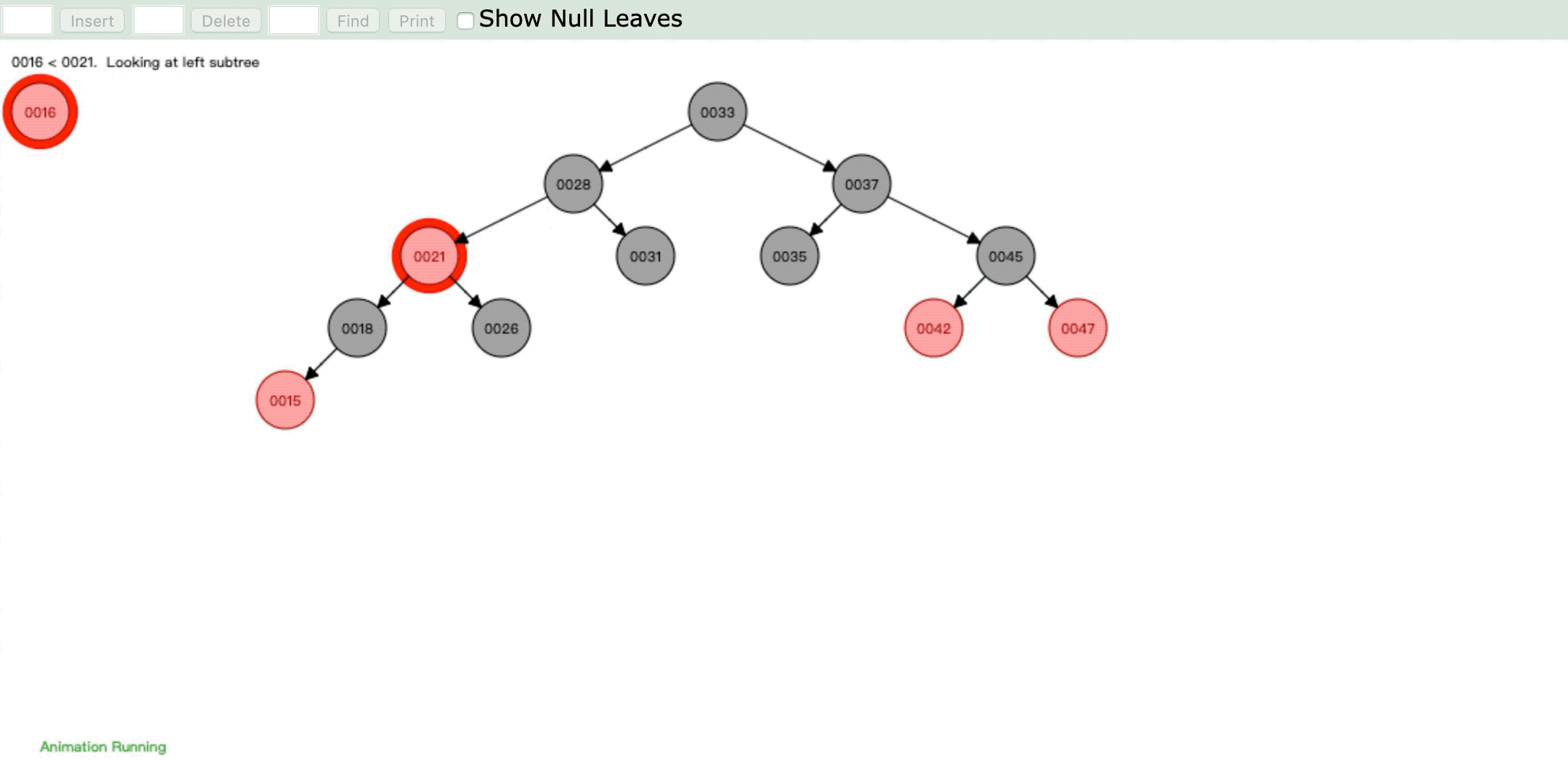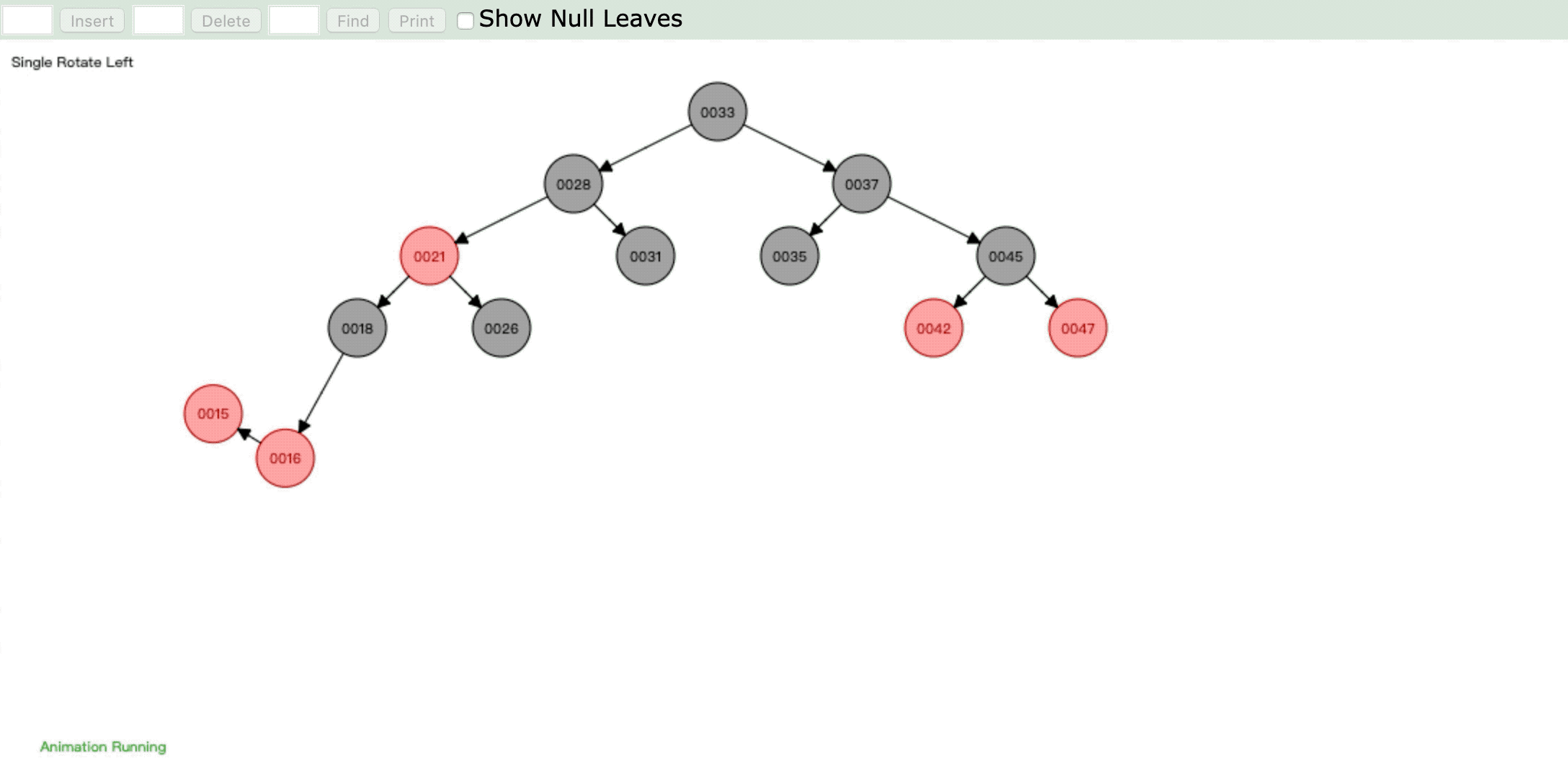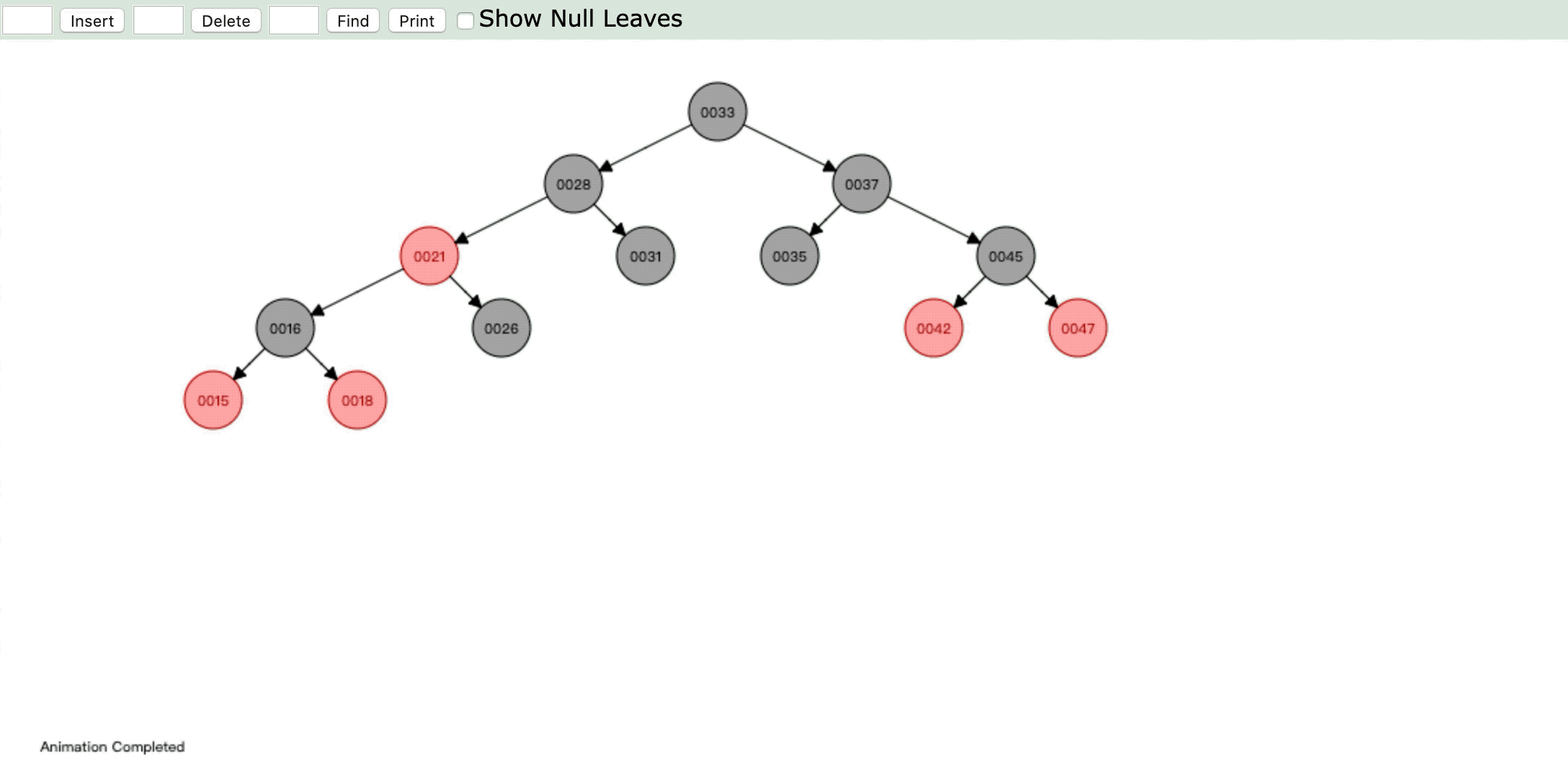
• 情形5：

操作：插入新节点，父节点是红色，叔父节点是黑色或缺省，新节点是左子节点，父节点又是其父节点的左子节点。

违反性质4：" 每个红色节点必须有两个黑色的子节点。 "

情形：父节点染色为黑色，进行右旋，祖父节点变为右子节点，然后重新判断进行染色或旋转

HashMap

结构

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
    TreeNode<K,V> parent;  // red-black tree links
    TreeNode<K,V> left;
    TreeNode<K,V> right;
    TreeNode<K,V> prev;    // needed to unlink next upon deletion
    boolean red;
    // ... 省略
}

三个参数

/**
 * 链表转为树阈值。
 * 大于等于8时，会转换为树。
 * 8 是综合性能考虑确定的值
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * 从树转换为链表的阈值
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * 最小树形化容量，只有哈希表元素数到达64才会进行树转换
 */
static final int MIN_TREEIFY_CAPACITY = 64;

链表转红黑树-treeifyBin

1. 数组（哈希表）长度到达64
2. 当链表长度大于等于8是会将链表转换为红黑树

final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    // 数组为null或者数组长度小于MIN_TREEIFY_CAPACITY（64）时，进行扩容
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        // 头尾节点 hd-头 tl-尾
        TreeNode<K,V> hd = null, tl = null;
        do {
            // 创建树节点 Node -> TreeNode
            // 循环执行完之后得到的是双向链表
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        // 此时得到的仅仅是双向链表
        // 指针指向链表头
        if ((tab[index] = hd) != null)
            // 将双向链表转换为树
            hd.treeify(tab);
    }
}

final void treeify(Node<K,V>[] tab) {
    TreeNode<K,V> root = null;
    for (TreeNode<K,V> x = this, next; x != null; x = next) {
        next = (TreeNode<K,V>)x.next;
        x.left = x.right = null;
        if (root == null) {
            // 情形1：插入第一个节点
            x.parent = null;
            x.red = false;
            root = x;
        }
        else {
            // 当前节点的 key 和 hash
            K k = x.key;
            int h = x.hash;
            Class<?> kc = null;
            // 再次循环
            for (TreeNode<K,V> p = root;;) {
                int dir, ph;
                // 内层循环的key
                K pk = p.key;
                // 当前节点的hash和内层循环的hash值作比较
                if ((ph = p.hash) > h)
                    // < 0 left查找
                    dir = -1;
                else if (ph < h)
                    // > 0 right 查找
                    dir = 1;
                else if ((kc == null &&
                            (kc = comparableClassFor(k)) == null) ||
                            (dir = compareComparables(kc, k, pk)) == 0)
                    // 比较对象
                    dir = tieBreakOrder(k, pk);

                TreeNode<K,V> xp = p;
                // dir <= 0 则走 left查找 > 0 则走 right查找
                if ((p = (dir <= 0) ? p.left : p.right) == null) {
                    x.parent = xp;
                    if (dir <= 0)
                        xp.left = x;
                    else
                        xp.right = x;
                    // 正式转换为红黑树
                    root = balanceInsertion(root, x);
                    break;
                }
            }
        }
    }
    moveRootToFront(tab, root);
}

// root 根节点
// x 要操作的节点
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) {
    // 默认节点为红色
    x.red = true;
    // xp：x的父节点
    // xpp：x的祖父节点
    // xppl：x祖父节点的左子节点
    // xppr：x祖父节点的右子节点
    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {

        // 情形1： 父节点为null， 直接置为根
        if ((xp = x.parent) == null) {
            x.red = false;
            return x;
        }
        // 父节点黑色 或者 祖父节点为空，直接返回
        // 情形2：插入新节点，父节点是黑色
        else if (!xp.red || (xpp = xp.parent) == null)
            return root;

        // 父节点是祖父节点的左子节点
        if (xp == (xppl = xpp.left)) {
            // 祖父节点的右子节点不为空且是红色
            // 情形3：插入新节点，父节点是红色，叔父节点是红色
            if ((xppr = xpp.right) != null && xppr.red) {
                xppr.red = false; //祖父节点的右子节点设置为黑色
                xp.red = false; // 父节点设置为黑色
                xpp.red = true; // 祖父节点设置为红色
                x = xpp; // 继续操作祖父节点
            }
            // 旋转
            else {
                // 新插入的是右子节点
                if (x == xp.right) {
                    // 插入的x是父节点的右子节点， 进行左旋
                    root = rotateLeft(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                if (xp != null) {
                    // 父节点设置为黑色
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        // 右旋
                        root = rotateRight(root, xpp);
                    }
                }
            }
        }
        // 父节点是祖父节点的右子节点
        else {
            // 祖父节点的左子节点不为空且为红色
            if (xppl != null && xppl.red) {
                xppl.red = false; // 祖父节点的左子节点设置为黑色
                xp.red = false; // 父节点设置为黑色
                xpp.red = true; // 祖父节点设置为红色
                x = xpp; // 继续操作祖父节点
            }
            // 旋转
            else {
                if (x == xp.left) {
                    root = rotateRight(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
}