2020杭电多校 10C / HDU 6879 - Mine Sweeper （构造）

HDU 6879 - Mine Sweeper

题意

定义《扫雷》游戏的地图中每个空白格子的值为其周围八个格子内地雷的数量（即游戏内临近地雷数量的提示）

则一张地图的值\(S\)为所有空白格子的值总和

现给定\(S\)，要求构造出一张长度与宽度均不超过\(25\)的地图，使其值等于\(S\)

限制

\(1\leq T\leq 1001\)

\(0\leq S\leq 1000\)

思路

这题过的人数应该是最多的，所以肯定是存在比我的想法更优更方便的解的

但是题解写的不是很清楚，所以还是写下了这篇博客（画图好累……）

发现\(T_{max}=|S|\)，范围内每个值肯定都会问一遍，考虑预处理所有方案（在线输出好像也没有问题的样子）

首先发现，如果一个地雷周围没有其他地雷，也没有障碍物（表示它不在图的边界上）

那么这个地雷对于答案的贡献就是\(8\)

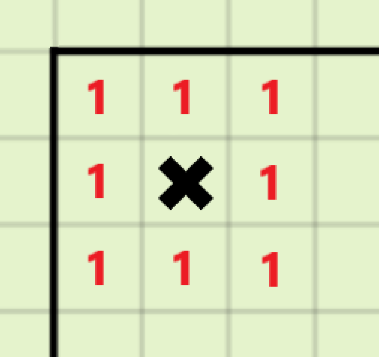
考虑所有地雷都互不相邻的情况（一个地雷周围一圈不存在其他地雷）

由于图最大尺寸为\(25\times 25\)

地雷分布情况为\((2,2),(2,4),\dots,(2,24),(4,2),(4,4),\dots,(24,24)\)

这样总共能放置\(12\times 12=144\)个对答案贡献为\(8\)的地雷

由于\(144\times 8>1000\)，这样的分布绰绰有余

所以得到一个结论：只要\(S\)为\(8\)的倍数，那么它一定有解

---

首先考虑\(S\lt 8\)的所有情况

当\(S=0\)时，直接输出一个\(1\times 1\)的空图即可

当\(S=1\)时

当\(S=2\)时

当\(S=3\)时

当\(S=4\)时

当\(S=5\)时

当\(S=6\)时

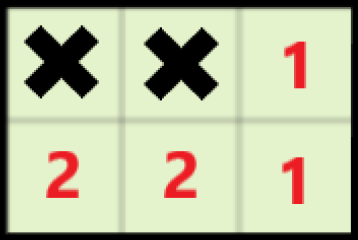
当\(S=7\)时

---

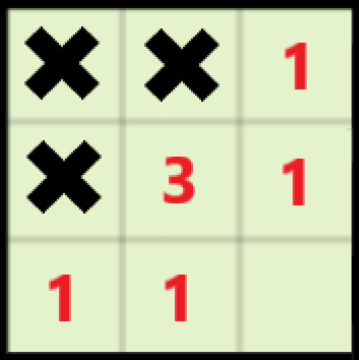
既然已经能够确定一个数的倍数一定有解了，那我们可以尝试找找看能否依托\(8\)来找出其他情况

也就是把\(S\geq 8\)的所有情况看成以下的形式之一表示

\[\left \{
\begin{aligned}
8&k\\
8&k+1\\
8&k+2\\
8&k+3\\
8&k+4\\
8&k+5\\
8&k+6\\
8&k+7\\
\end{aligned}
\right \}
,\ k\in \Z
\]

---

对于\(S=8k+1\)的情况：

在\((1,1)\)的位置多放置一个地雷，可以使得原本位于\((2,2)\)的地雷对答案的贡献由\(8\)变成\(9\)，且不影响其他地雷的贡献

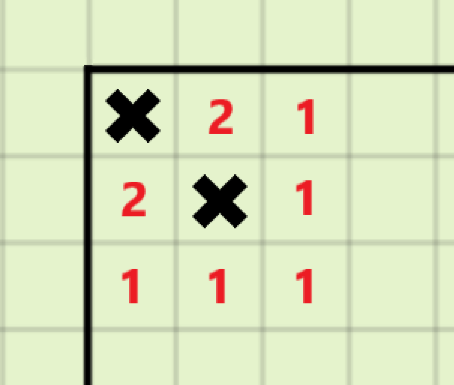
对于\(S=8k+2\)的情况：

在\((1,1)\)与\((1,2)\)的位置多放置两个地雷，可以使得原本位于\((2,2)\)的地雷对答案的贡献由\(8\)变成\(10\)，且不影响其他地雷的贡献

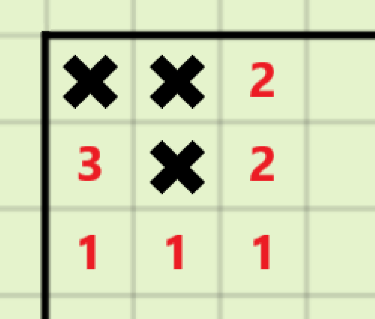
对于\(S=8k+3\)的情况：

在\((1,2)\)的位置多放置一个地雷，可以使得原本位于\((2,2)\)的地雷对答案的贡献由\(8\)变成\(11\)，且不影响其他地雷的贡献

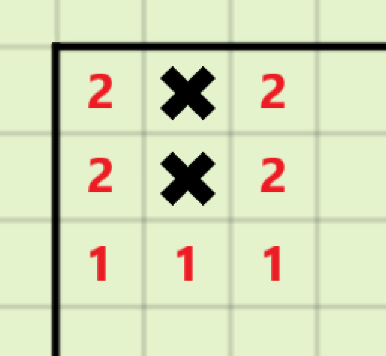
对于\(S=8k+4\)的情况：

在\((1,2)\)与\((2,1)\)的位置多放置两个地雷，可以使得原本位于\((2,2)\)的地雷对答案的贡献由\(8\)变成\(12\)，且不影响其他地雷的贡献

对于\(S=8k+5\)的情况：

仅先看放置贡献为\(8\)的地雷，假设最后一个放置的地雷位于第\(i\)行

为了不影响它对答案的贡献，那么第\(i+1\)行不能放东西

由上面\(S=5\)的情况可得，我们可以将其上下倒置放在第\(i+2\)行，从而防止其对其他地雷贡献造成影响

（边界限制可行性证明在下面）

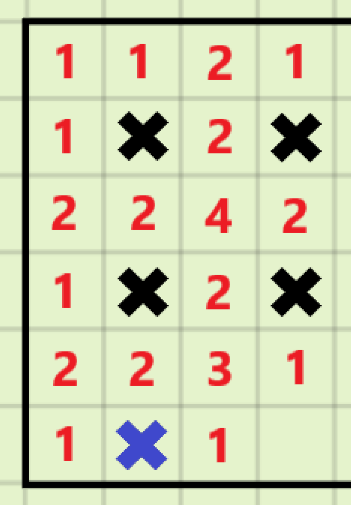
对于\(S=8k+6\)的情况：

参考\(S=6\)，同样的，为了不产生冲突，只能放置在第\(i+2\)行

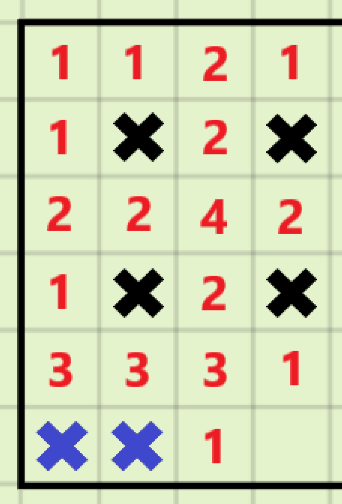
对于\(S=8k+7\)的情况：

由于\(S=7\)的情况里地雷需要占两行

所以要将\(S=7\)的情况倒置放在\(S=8k\)的第\(i+2\)行与第\(i+3\)行

（边界限制可行性证明在下面）

---

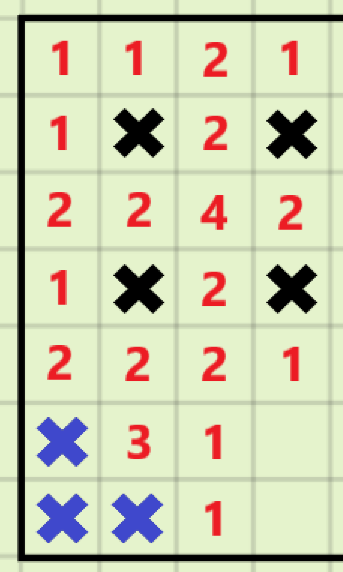
直接证明\(S=8k+7\)时需要用到\(i+3\)行的可行性情况吧

由于\(S\)最大为\(1000\)，如果全部使用贡献为\(8\)的地雷方案填充地图，最多只需要\(125\)个地雷

每行最多能放置\(12\)个这种方案的地雷，那么最多只需要用到第\(11\)行过

对于原图，由于地雷在行之间也需要空一行，故\(i\)的最大值为\(22\)

\(22+3=25\)，恰好满足题目要求，故方案可行

---

综上，本题所有\(S\)情况均有解，预处理后直接输出即可

注意，\(S=8k\)的情况最后也需要输出\(i+1\)行（最后一行空着，以保证有空格子让地雷做出贡献，即让最后一行的地雷非边界）

示例

如果没大看懂上面的例子，这里放几张截图领会一下大致意思即可

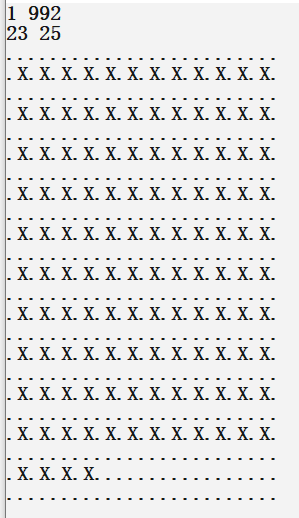
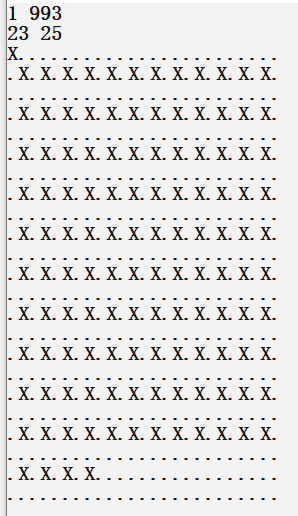
代码

(0ms~31ms/1000ms)

#include<bits/stdc++.h>
using namespace std;

int mp[1010][28][28];
int maxCol[1010];

void init()
{
    for(int i=8;i<=1000;i++)
    {
        int les=i/8,j,k;
        for(j=2;j<=24;j+=2)
        {
            for(k=2;k<=24;k+=2)
            {
                mp[i][j][k]=1;
                if(--les==0)
                    break;
            }
            if(les==0)
                break;
        }
        switch(i%8)
        {
            case 0:
                maxCol[i]=j+1;
                break;
            case 1:
                mp[i][1][1]=1;
                maxCol[i]=j+1;
                break;
            case 2:
                mp[i][1][1]=mp[i][1][2]=1;
                maxCol[i]=j+1;
                break;
            case 3:
                mp[i][1][2]=1;
                maxCol[i]=j+1;
                break;
            case 4:
                mp[i][1][2]=mp[i][2][1]=1;
                maxCol[i]=j+1;
                break;
            case 5:
                mp[i][j+2][2]=1;
                maxCol[i]=j+2;
                break;
            case 6:
                mp[i][j+2][1]=mp[i][j+2][2]=1;
                maxCol[i]=j+2;
                break;
            case 7:
                mp[i][j+3][1]=mp[i][j+3][2]=mp[i][j+2][1]=1;
                maxCol[i]=j+3;
                break;
        }
    }
}

int main()
{
    init();
    int T,S;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&S);
        if(S>=8)
        {
            printf("%d 25\n",maxCol[S]);
            for(int i=1;i<=maxCol[S];i++)
            {
                for(int j=1;j<=25;j++)
                {
                    if(mp[S][i][j])
                        putchar('X');
                    else
                        putchar('.');
                }
                putchar('\n');
            }
        }
        else if(S==0)
        {
            puts("1 1");
            puts(".");
        }
        else if(S==1)
        {
            puts("1 2");
            puts("X.");
        }
        else if(S==2)
        {
            puts("1 3");
            puts("X.X");
        }
        else if(S==3)
        {
            puts("2 2");
            puts("X.");
            puts("..");
        }
        else if(S==4)
        {
            puts("2 2");
            puts("X.");
            puts("X.");
        }
        else if(S==5)
        {
            puts("2 3");
            puts(".X.");
            puts("...");
        }
        else if(S==6)
        {
            puts("2 3");
            puts("XX.");
            puts("...");
        }
        else if(S==7)
        {
            puts("3 3");
            puts("XX.");
            puts("X..");
            puts("...");
        }
    }
    return 0;
}