[算法入门]——深度优先搜索（DFS）

深度优先搜索（DFS）

深度优先搜索叫DFS（Depth First Search）。OK，那么什么是深度优先搜索呢?_?

---

样例：

举个例子，你在一个方格网络中，可以简单理解为我们的地图，要从A点到B点找到最短路径：

我们要制定一个策略，以此来建立递归函数。在这种情况下，先往右一直走或往下走，如果往上走或往左走，便必然得不到最优解。

此时你从A点出发，一直朝着右走：

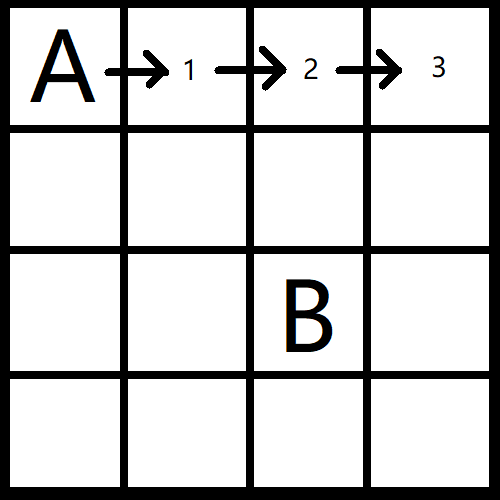
发现右边已经没有可以访问的节点了，再选择朝下递归：

此时找不到可以往右走或往下走的点了，所以只好返回，一直返回到第一个可用节点：

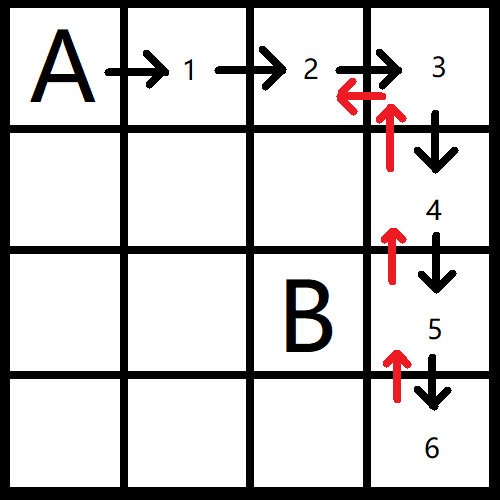
如上重复，在朝下递归：

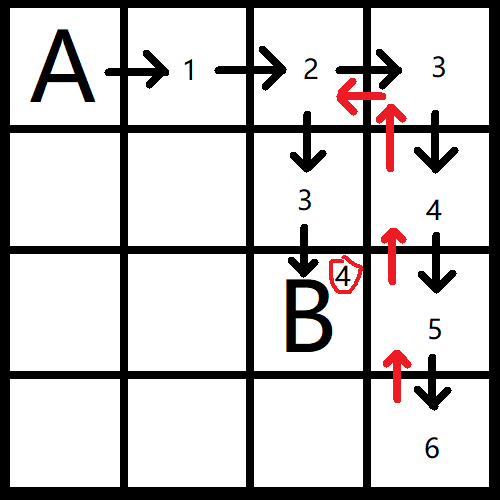
我们便得到了一个答案：4！虽然程序实际运行情况不会这么简单，所以有时需要考虑更加周到一点。但是我们知道这么多就够了。（你甚至可以写个断点来看它到底干了啥）。

以此，我们可以大体总结一下深度优先搜索的一个基本思想：从一个节点出发，一直到找不到可行节点时，再选择返回。

深度优先搜索是建立在以栈为基础的算法，而递归又恰好符合这个特性，我们可以大致写出深度优先搜索的伪代码：

void dfs(所走的次数, 其他参数)
{
    if (找到了符合条件的节点)
    {
        //更新最小值
        return;
    }
    for (遍历所有方法)
    {　
  　　   //如果找到了一个可行节点，便递归到下一个栈帧
        if (该方法可行)
        {
            dfs(所走次数 + , 其他参数);
        }
    }
}

但是这样子写会有一个问题：同样的一个节点会被走很多次！这还不是最可怕的，在没有总结出 “如果往上走或往左走，便必然得不到最优解” 的情况下，甚至可能会出现程序放飞自我，A->B，然后B->A，如此死循环然后栈溢出。我们只好引用一个二维数组，只要走过这个节点便对其进行标记表示这里走过了，往后的递归就不能再访问此节点，来避免A->B B->A的尴尬情况。

void dfs(所走的次数, 其他参数)
{
    if (找到了符合条件的节点)
    {
        //更新最小值
        return;
    }
    for (遍历所有方法)
    {
        if (该方法可行)
        {
            //标记该节点走过
            dfs(所走次数 + , 其他参数);
            //回溯：将该节点标记未走过
        }
    }
}

既然我们写出了代码，为什么还要进行一个叫“回溯(sù)”的事情呢？我们写代码时不能保证一定可以得到最优解，或许从一条路搜索过来需要走5次，从另一条路走过来只要3次。如果没有回溯的话，就会使走过的节点无法再走，更优的解无法覆盖原来的解，需要3次的走法就无法覆盖只需要5次的走法，从而得不到最优解。尽管如此，深度优先搜索的时间开支依旧不小。再打个比方，你已经知道走这条路不是最优解了，但你还是不得不把它走完。所以，我们就需要用到剪枝来剔除不必要的搜索。在这里，剪枝方案就是：如果当前所使用的步数，已经大于等于到终点的所需的步数，那么就舍去这条路线。因为从此处为起点出发的任何一个节点都不可能是最优解了。

int ans = 0x7f7f7f7f //答案，初始值可以看做无限大
void dfs(所走的次数, 其他参数)
{
    if (所走的次数 > ans)
    {
        return;
    }
    if (找到了符合条件的节点)
    {
        //更新最小值
        return;
    }
    for (遍历所有方法)
    {
        if (该方法可行)
        {
            //标记该节点走过
            dfs(所走次数 + , 其他参数);
            //回溯：将该节点标记未走过
        }
    }
}

这样，就是一个标准的深度优先搜索模板。我们也可以针对其他例题进行修改（有些情况甚至连剪枝都剪不了）。

---

例题（洛谷P2404）：

现在引入一道例题：

题目描述

任何一个大于1的自然数n，总可以拆分成若干个小于n的自然数之和。现在给你一个自然数n，要求你求出n的拆分成一些数字的和。每个拆分后的序列中的数字从小到大排序。然后你需要输出这些序列，其中字典序小的序列需要优先输出。

输入格式

输入：待拆分的自然数n。

输出格式

输出：若干数的加法式子。

输入输出样例

输入 #1

7

输出 #1

1+1+1+1+1+1+1

1+1+1+1+1+2

1+1+1+1+3

1+1+1+2+2

1+1+1+4

1+1+2+3

1+1+5

1+2+2+2

1+2+4

1+3+3

1+6

2+2+3

2+5

3+4

 

条件：

n ≤ 8

分析一下题目，不难发现，输出样例中，每一行（每一组解）后面的数字一定不小于前面的数字，并且所有数字之和一定等于且不大于n，那么我们可以大致分析出dfs的参数：

//从左到右的参数依次为：不能小于该数，现在选择第几个数字，数字之和
void dfs(int num, int now, int sum)
{
　　...
}

其中的num可以简化略掉，但是为了方便阅读还是加上去了。

那么，我们还需要一个数组来保存所找到的解，我们把它定义为s[10]。题目中n不会大于8，但是为了避免一些奇奇怪怪的错误，故开为10。很多以索引为1开头的写法，都推荐把数组开大一点（反正评测姬上的内存也不是自家的）。

//s数组用来存储当前的解。题目中给定n不可能大于8，但是为了避免一些奇怪的错误，故将数组s开大一点
int s[], n; 

那么，如何判断是否找到了一个可行解呢？其实不难，当参数sum刚好等于n时，即可输出答案（不是大于等于），这样就无需去计算当期解的和，减少运算量。

//找到了一个可行解便打印出来
if (sum == n)
{
    for (int i = ;i < now - ;i++)
        printf ("%d+", s[i]);
    printf ("%d\n", s[now - ]);
    return;
}

那么接下来就是枚举所有可行的数字，此时num就派上用场了：接下来可行的数字一定在num到n之间。而now就是存储当前操作第几个数字的索引（索引听不懂的回去补课）

//遍历所有可行数字，如果是i<=n的话，深搜到最后会将n自己打印出来
for (int i = num;i < n;i++)
{
    s[now] = i;
    dfs(i, now + , sum + i);
    s[now] = ;        //此行可省略
}

代码中第6行可以省略。为什么可以省略呢？因为以我们的写法，是不会再次访问s[now]的，所以就没必要回溯。

全部代码：

#include <cstdio>
//s数组用来存储当前的解。题目中给定n不可能大于8，但是为了避免一些奇怪的错误，故将数组s开大一点
int s[], n;
//从左到右的参数依次为：不能小于该数，现在选择第几个数字，数字之和
void dfs(int num, int now, int sum)
{
    //如果总和超过了n，就直接返回
    if (sum > n)
        return;
    //找到了一个可行解便打印出来
    if (sum == n)
    {
        for (int i = ;i < now - ;i++)
            printf ("%d+", s[i]);
        printf ("%d\n", s[now - ]);
        return;
    }
    //遍历所有可行数字，如果是i<=n的话，深搜到最后会将n自己打印出来
    for (int i = num;i < n;i++)
    {
        s[now] = i;
        dfs(i, now + , sum + i);
        s[now] = ;        //此行可省略
    }
}
int main()
{
    scanf ("%d", &n);
    dfs(, , );
    return ;
}

---

总结：

深度优先搜索其中函数很好写，但是大体思路有一点难以理解，甚至会出现玄学代码的情况（改一个符号便出现完全例外的情况），所以写代码的时候要尽可能严谨，并且不要乱剪枝。深度优先搜索本质上是一个暴力算法，并且多以递归+回溯的形式出现，如果优化和剪枝不好并且数据刁钻，经常出现TLE的情况。

题外话：

这是我写的第一个博客，可能会出现一些奇奇怪怪的错误，不过可以在评论区留言，我一定会改的（艾玛好紧张QAQ）