3.29省选模拟赛 除法与取模 dp+组合计数

LINK：除法与取模

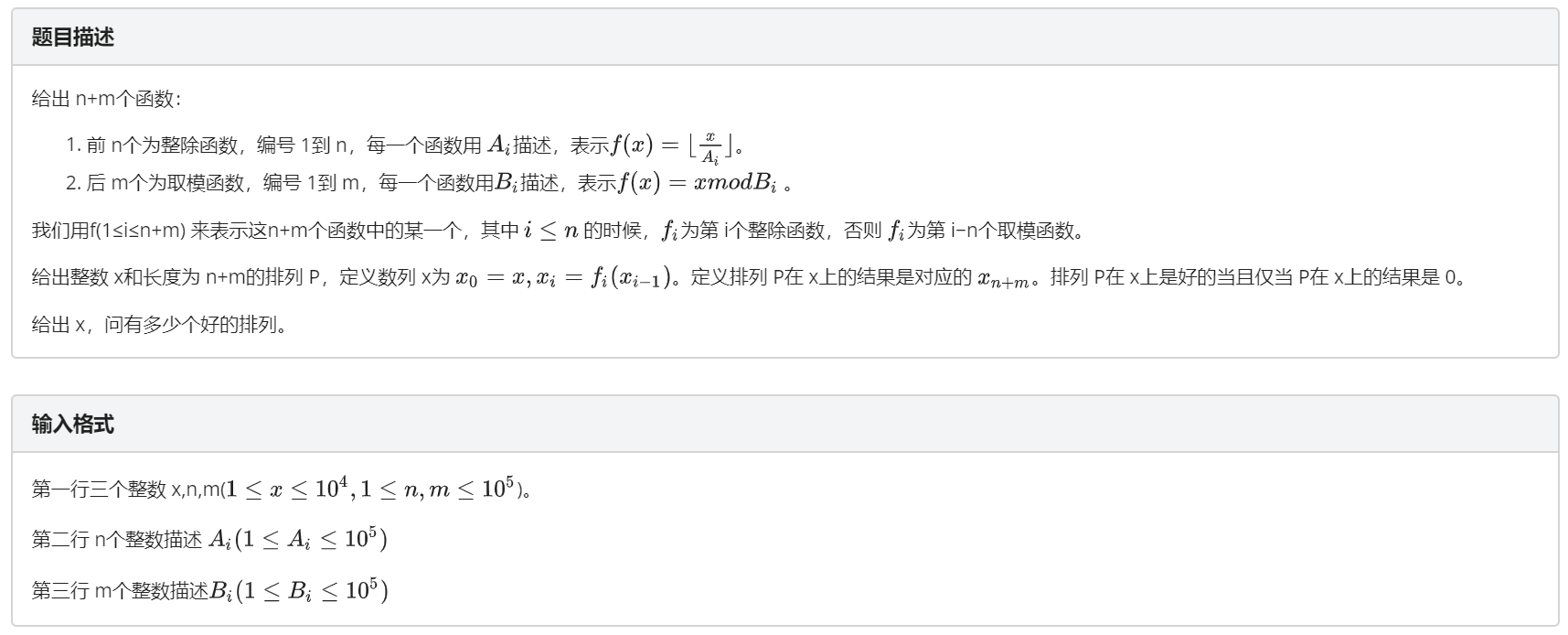
鬼题。不过50分很好写。考虑不带除法的时候 其实是一个dp的组合计数。

考虑带除法的时候需要状压一下除法操作。

因为除法操作是不受x的大小影响的 所以要状压这个除法操作。

直接采用二进制状压是不明智的 2的个数最多为13个 2^13也同样到达了1e4的复杂度。

考虑 hash状压 即 2的个数有x个 那么我们就有状态w表示2还有x个。

这样做的原因是把一些相同的东西给合并起来 而并非分散开来。即有多个2直接记录有多少个即可。

可以发现 这样做不同的除数最多只有5个 状态量较少。

如何hash 考虑采用P进制版本的hash 这样寻找下一个决策什么的也很方便。

如：对于第i个数 进制为(当前个数+1) 这样不需要取模我们的状态量也只有不到100.

可以发现这样的hash不重不漏 缺点是 我们需要知道某个状态代表的是什么意思 去掉某个值后 得到的状态会是什么。

这样做x状态数状态转移+x状态x当前的值.

前者复杂度极低 后者 考虑第一步做的时候 x会除以2所以一半都不需要枚举了 且后面的那个x当前的值也会降低一半 一下就变成了50005000状态的dp了。

第二部做的时候还会除以2 可以发现无效的状态很多我们对于无效的状态不枚举转移即可。

(题解上说是有一个1/16的常数 所以可以通过此题。

dp的时候转移比较ex 值得注意的是 %一个数字或者除以一个数字的时候 如果有重复的存在必须要处理一下相对的关系。

前者 要乘以h[w]//w出现了多少次 因为取模过后剩余的数字被安排过了。那些数字之间不存在先后 因为是排列过的。

后者 发现此时的选择也同样有g[j][w]种 要乘上这个东西的方案。

hash的时候要注意 某个数的0的个数时的状态表示。dp的时候注意两层循环都要倒序枚举。

一道非常优异的dp题目。

const int MAXN=200010,maxn=10010;
int a[MAXN],b[MAXN],q[MAXN],c[MAXN],w[MAXN],p[MAXN],vis[MAXN];
ll fac[MAXN<<1],inv[MAXN],in[MAXN],f[maxn][110];
int g[MAXN][10],v[MAXN],h[MAXN];
int n,m,maxx,s,top,sum,tot;
inline ll ksm(ll b,int p)
{
	ll cnt=1;
	while(p)
	{
		if(p&1)cnt=cnt*b%mod;
		b=b*b%mod;p=p>>1;
	}
	return cnt;
}
inline void prepare()
{
	fac[0]=1;in[1]=1;
	rep(1,maxx,i)
	{
		fac[i]=fac[i-1]*i%mod;
		if(i!=1)in[i]=(mod-mod/i)*in[mod%i]%mod;
	}
	inv[maxx]=ksm(fac[maxx],mod-2);
	fep(maxx-1,0,i)inv[i]=inv[i+1]*(i+1)%mod;
}
inline void get_state()
{
	int ww=0;
	rep(1,sum,i)ww=ww*(w[i]+1)+q[i];
	tot=max(tot,ww);
	rep(1,sum,i)g[ww][i]=q[i],v[ww]+=q[i];
}
inline void dfs(int x)
{
	if(x==sum+1)
	{
		get_state();
		return;
	}
	rep(0,w[x],i)
	{
		q[x]=i;
		dfs(x+1);
	}
}
int main()
{
	freopen("1.in","r",stdin);
	get(s);get(n);get(m);maxx=n+m;
	prepare();
	rep(1,n,i)
	{
		get(a[i]);
		if(a[i]>s){putl(fac[n+m]);return 0;}
	}
	ll ww=1;
	rep(1,n,i)
	{
		if(a[i]>1)q[++top]=a[i];
		ww=ww*a[i];
		if(ww>s){putl(fac[n+m]);return 0;}
	}
	sort(q+1,q+1+top);
	rep(1,top,i)
	{
		if(q[i]==q[i-1])++w[sum],++i;
		if(i<=top)c[++sum]=q[i],++w[sum];
	}
	p[sum]=1;
	fep(sum-1,1,i)p[i]=p[i+1]*(w[i]+1);
	dfs(1);//整理状态
	rep(1,m,i)get(b[i]),++vis[min(b[i],s+1)],++h[b[i]];
	rep(1,s+1,i)vis[i]+=vis[i-1];
	f[s][tot]=fac[n+m]*inv[n+m-(vis[s+1]-vis[s])-(n-top)]%mod;
	fep(s,0,i)
	{
		//if(i==0)cout<<"www"<<endl;
		fep(tot,0,j)
		{
			if(!f[i][j])continue;
			//枚举要取模的数字.
			rep(1,i,k)
			{
				if(!h[k])continue;
				//当前还有数字为 v[j]+vis[i]-1
				//剩余有效数字为 v[j]+vis[i%k]
				f[i%k][j]=(f[i%k][j]+h[k]*f[i][j]%mod*fac[v[j]+vis[i]-1]%mod*inv[v[j]+vis[i%k]]%mod)%mod;
			}
			rep(1,sum,k)//枚举要除以的数字.
			{
				if(g[j][k])
				{
					//当前还有数字为 v[j]-1+vis[i]
					//剩余有效数字为 v[j]-1+vis[i/c[k]]
					f[i/c[k]][j-p[k]]=(f[i/c[k]][j-p[k]]+g[j][k]*f[i][j]%mod*fac[v[j]-1+vis[i]]%mod*inv[v[j]-1+vis[i/c[k]]]%mod)%mod;
				}
			}
		}
	}
	/*fep(s,0,i)
	{
		cout<<i<<' '<<"www"<<' ';
		fep(tot,0,j)
		cout<<f[i][j]<<' ';
		cout<<endl;
	}*/
	putl(f[0][0]);
	return 0;
}