BZOJ 2154: Crash的数字表格 [莫比乌斯反演]

2154: Crash的数字表格

Time Limit: 20 Sec  Memory Limit: 259 MB
Submit: 2924  Solved: 1091
[Submit][Status][Discuss]

Description

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

Input

输入的第一行包含两个正整数，分别表示N和M。

Output

输出一个正整数，表示表格中所有数的和mod 20101009的值。

Sample Input

4 5

Sample Output

122
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。

---

计算所有lcm(i,j)的和

 

考虑每个gcd的取值，

 

那么可以得到

ans=Σ{d=1...min(n,m)}f(n,m,d)/d 进一步改写方便分块

 

(原因：考虑所有gcd(i,j)=k的i和j都是ii*k和jj*k且gcd(ii,jj)=1)

 

问题就是求解f函数，发现f函数和bzoj2301中用的“

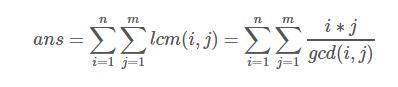
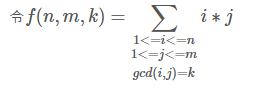
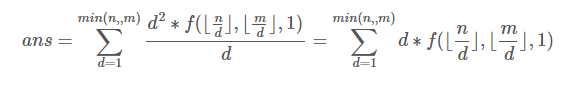
• f(i)为1<=x<=n,1<=y<=m且gcd(x,y)=i的数对(x,y)的个数

”很像，这个不是个数而是i*j的和，同样考虑莫比乌斯反演

构造F(x,y,k)为k|gcd(i,j)的i*j和，想办法直接算出F

 

 

(原因：k|gcd(i,j) --> 所有的k的倍数)

 

莫比乌斯反演

 

ans需要的部分即为

 

我们发现ans的部分用f可以sqrt(n)分块，求f的时候又可以sqrt(n)分块(处理mu[i]*i*i前缀和)，总共O(n)

 

 

经验：

需要f(x,y,1)想的时候不要只想1，这样并不好就行莫比乌斯反演

 

注意：

前缀和要用ll，然而本题int也没问题

 

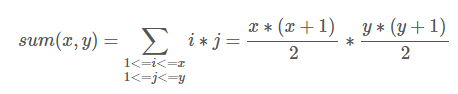
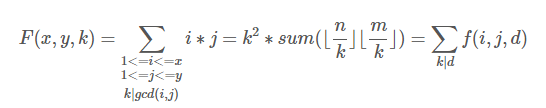
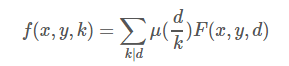
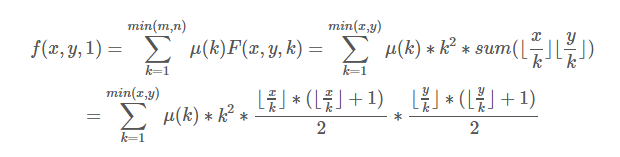
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=1e7+,MOD=;
inline int read() {
    char c=getchar();
    int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int n,m;
bool notp[N];int p[N];
ll s[N],mu[N];
void sieve(int n){
    mu[]=;
    for(int i=;i<=n;i++){
        if(!notp[i]) p[++p[]]=i,mu[i]=-;
        for(int j=;j<=p[]&&i*p[j]<=n;j++){
            int t=i*p[j];
            notp[t]=;
            if(i%p[j]==){
                mu[t]=;
                break;
            }
            mu[t]=-mu[i];
        }
    }
    for(ll i=;i<=n;i++)
     s[i]=(s[i-]+(i*i*mu[i])%MOD)%MOD;
}
inline ll S(ll x,ll y){
    return ((x*(x+)/)%MOD)*((y*(y+)/)%MOD)%MOD;
}
ll f(ll n,ll m){
    ll ans=,r=;
    for(ll d=;d<=n;d=r+){
        r=min(n/(n/d),m/(m/d));
        ans=(ans+(s[r]-s[d-])*S(n/d,m/d)%MOD)%MOD;
    }
    return ans;
}
int main() {
    n=read();
    m=read();
    sieve(n);
    if(n>m) swap(n,m);
    ll ans=,r=;
    for(ll d=;d<=n;d=r+){
        r=min(n/(n/d),m/(m/d));
        ans=(ans+f(n/d,m/d)*((r-d+)*(r+d)/)%MOD)%MOD;
    }
    printf("%lld",(ans+MOD)%MOD);

}