自适应滤波：维纳滤波器——GSC算法及语音增强

作者：桂。

时间：2017-03-26  06:06:44

链接：http://www.cnblogs.com/xingshansi/p/6621185.html

声明：欢迎被转载，不过记得注明出处哦~

---

【读书笔记04】

前言

仍然是西蒙.赫金的《自适应滤波器原理》第四版第二章，首先看到无约束维纳滤波，接着到了一般约束条件的滤波，此处为约束扩展的维纳滤波，全文包括：

　　1）背景介绍；

　　2）广义旁瓣相消（Generalized Sidelobe Cancellation, GSC）理论推导；

　　3）GSC应用——语音阵列信号增强；

内容为自己的学习记录，其中错误之处，还请各位帮忙指正！

一、背景介绍

在一般约束条件的维纳滤波中，有${{\bf{w}}^H}{\bf{s}}\left( {{\theta _0}} \right) = g$的约束条件，即${{\bf{s}}^H}\left( {{\theta _0}} \right){\bf{w}} = g$.如${\bf{s}}\left( {{\theta _0}} \right)$为旋转向量时，希望在$\theta _0$处保留波束—>对应$g_1  = 1$，希望在$\theta_2$处抑制波束—>对应$g_2 = 0$，写成一般形式：

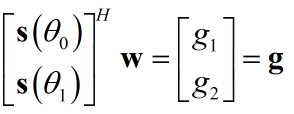
写成更一般的形式：

${{\bf{C}}^H}{\bf{w}} = {\bf{g}}$

假设$\bf{w}$权值个数为M，在一般约束维纳滤波中可以看出：限定条件使得结果更符合预期的效果。假设C为M×L的矩阵：L个线性约束条件。对于M个变量的方程组，对应唯一解最多有M个方程，即：对于L个线性约束来讲，我们仍可以继续利用剩下的M-L个自由度进行约束，使得结果更加符合需求（比如增强某信号、抑制某信号等），这便是GSC的背景。

二、GSC理论推导

　　A-理论介绍

书中的推导较为繁琐，我们可以从投影空间的角度加以理解，也就是最小二乘结果的矩阵求逆形式，给出简要说明：

对于矩阵A（N×M）:

• 如果A是满列秩（N>=M）对于符合LA=I的矩阵解为：${\bf{L}} = {\left( {{{\bf{A}}^H}{\bf{A}}} \right)^{ - 1}}{{\bf{A}}^H}$;
• 如果A是满行秩（N<=M）对于符合AR=I的矩阵解为：${\bf{R}} = {{\bf{A}}^H}{\left( {{{\bf{A}}}{\bf{A}^H}} \right)^{ - 1}}$.

对于${{\bf{C}}^H}{\bf{w}} = {\bf{g}}$，得出最优解：

${{\bf{w}}_q} = {\bf{C}}{\left( {{{\bf{C}}^H}{\bf{C}}} \right)^{ - 1}}{\bf{g}}$

记：

${{\bf{w}}_{re}} = {\bf{w}} - {{\bf{w}}_q}$

为了便于对余量${{\bf{w}}_{re}}$进行控制，将C扩展为：[ C | C$_{a}$ ]，$\bf{C}_a$的列向量为矩阵C列向量张成空间的正交补空间的基，即：

${\bf{C}}_a^H{\bf{C}} = {\bf{0}}$

分析新的空间特性：

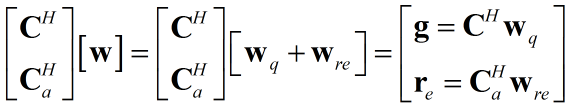
上式有${{\bf{C}}^H}{{\bf{w}}_{re}} = {\bf{0}}$，这就说明只要满足该条件，${{\bf{r}}_e} = {\bf{C}}_a^H{{\bf{w}}_{re}}$就是补空间的余量，如何保证一定有${{\bf{C}}^H}{{\bf{w}}_{re}} = {\bf{0}}$呢？可以将${{{\bf{w}}_{re}}}$写为：${ - {{\bf{C}}_a}{{\bf{w}}_a}}$的形式，之所以添加$-$可能是因为正交补空间可以认为C列向量空间不能表征的成分，我们通常认为这一部分为该丢弃的残差，也因为是残差：${{\bf{C}}_a}$通常被称为阻塞矩阵（取Block之意）,很多书籍用$\bf{B}$表示。

重新给出推导的结果：

${\bf{w}} = {{\bf{w}}_q} - {{\bf{C}}_a}{{\bf{w}}_a}$       s.t. ${{\bf{C}}_a}{{\bf{w}}_q} = {\bf{0}}$

对应结构图为：

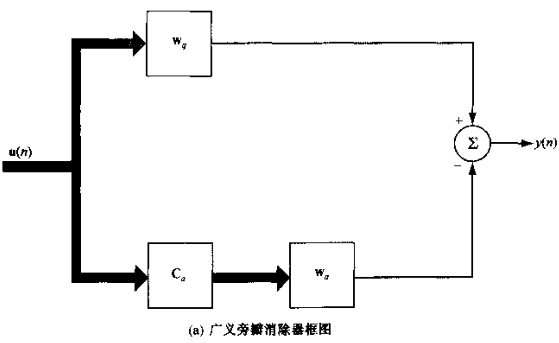
简化后可以认为上支、下支：

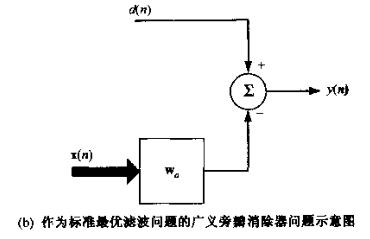
这是维纳滤波器的典型结构。

　　B-阻塞矩阵的选取

阻塞矩阵这一段摘自：秦博雅《基于低复杂度自适应信号处理的波束成形技术研究》p22~23.

大致有以下几种方式：

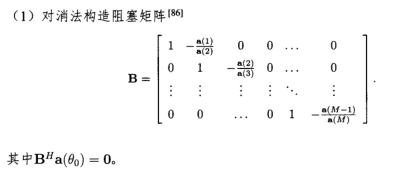
三、阵列信号增强

学了这个GSC怎么应用呢？这里参考一篇07年adaptive beamforming（引用见最后的参考）的例子，简要说明思路，关于阻塞矩阵。

文中结构图：

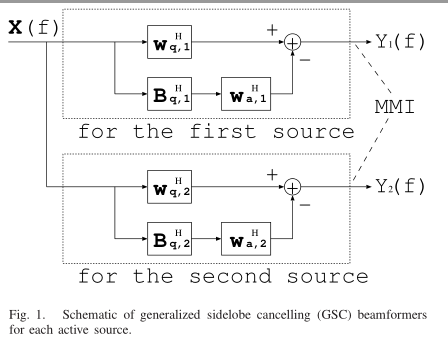
即：分别利用GSC框架，通过最小互信息实现信号的分离，其中$w_a$、$C_a$即$B$都提前给定，优化$w_{a1}$、$w_{a2}$。

定义互信息：

其中，

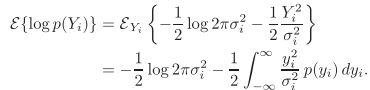
在幅度（严格来讲是傅里叶系数幅度）为正态条件下，得到：

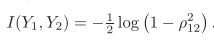
给出输出表达式：

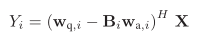
并给出准则函数——相关系数的表达式：

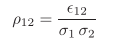
其中，

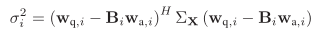
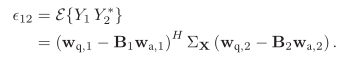
其中相关、互相关无法得到统计信息，仍然可以基于遍历性假设：利用时间换取空间，近似求取。

文中提到引入正则化（regularization）

这个只是优化过程中的限定条件，与GSC框架关系不大，不再补充。

这里在网上找去了一个8通道（channel）的混合语音（两个说话人），利用该算法进行分析，给出主要代码：

主要代码：

MMI_define_var(Xf1,Xf2);
%initialization
W1 = [0 0 0 0.1 0 0 0.2 ];
W2 = [0 2 0 0 0.2 0 0.1 ];
[Wa1,Wa2]=MMI_EstimateWa([W1 W2]');

其中MMI_define_var定义变量:

function MMI_define_var(Xf1,Xf2)

global Wq B covX1X1 covX2X2  covX1X2  len;

Wq=[1 1 1 1 1 1 1 1]'*1/8;
B=[1 -1 0 0 0 0 0 0 ;0 1 -1 0 0 0 0 0 ;0 0 1 -1 0 0 0 0 ;0 0 0 1 -1 0 0 0 ;0 0 0 0 1 -1 0 0 ;0 0 0 0 0 1 -1 0 ;0 0 0 0 0 0 1 -1 ]';

[~,len]=size(Xf2);
XfMean1=mean(Xf1.');
XfMean2=mean(Xf2.');
for i=1:8
    Xf1(i,:)=Xf1(i,:)-XfMean1(i);
    Xf2(i,:)=Xf2(i,:)-XfMean2(i);
end

covX1X1=Xf1*Xf1'/len;
covX2X2=Xf2*Xf2'/len;
covX1X2=Xf1*Xf2'/len;

MMI_EstimateWa实现参数估计:

function [Wa1 Wa2]=MMI_EstimateWa(W)
%obtain the Wa
ww=[real(W)' imag(W)']';

options = optimset('LargeScale','off','display','off');
[X,fval] = fminunc('MMI_real_imag_objfun',ww,options);
X_real=X(1:14);
X_imag=X(15:28);
Wa1_real=X_real(1:7);
Wa1_imag=X_imag(1:7);
Wa2_real=X_real(8:14);
Wa2_imag=X_imag(8:14);

Wa1=Wa1_real+sqrt(-1)*Wa1_imag;
Wa2=Wa2_real+sqrt(-1)*Wa2_imag;
end

对应结果图：

可以听出来：虽然略有杂音，但两个说话人的声音已经实现了分离，GSC框架有效。如果不同说话人声达时间估计准确，迭代算法应用合适，效果会更好，此处主要介绍GSC应用，细节不再琢磨，有兴趣的可以探索探索。

参考：

• K. Kumatani, T. Gehrig, U. Mayer, E. Stoimenov, J. McDonough and M. WÖlfel, "Adaptive Beamforming With a Minimum Mutual Information Criterion," in IEEE Transactions on Audio, Speech, and Language Processing, vol. 15, no. 8, pp. 2527-2541, Nov. 2007.
• Simon Haykin 《Adaptive Filter Theory Fourth Edition》.