2.2 logistic回归

1. logistic回归，是一个学习算法，用在监督学习问题中，
   1. 输出标签y是0或者1的时候，这是一个二元分类问题，
2. 给定一个输入x，一张图，你希望识别出这是不是猫图，
   1. 需要一个算法，可以给出一个预测值，我们说y^就是你对y的预测，更正式的说，你希望y^是一个概率，当输入特征x满足条件的时候y就是1，所以换句话说，如果x是图片，你希望y^能够告诉你，这是一张猫图的概率，
   2. x是一个nx维度的向量，已知logistic回归的参数是w，也是一个nx维度的向量，而b就是一个实数，
      1. 所以，已知输入x和参数w，b，我们如何计算输出预测y^呢？
         1. 可以使用线性回归，但是这不是一个非常好的二元分类算法y^=w^TX+b
         2. 所以在logistic回归中，我们的输出变成，y^等于sigmoid函数作用在w^TX+b这个量上面，这就是sigmoid函数的图形，
            1. 
            2. 这个就是sigmoid函数的公式，
               1. 
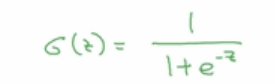
               2. 如果z非常大，那么e^(-z)就很接近0，结果就接近于1
               3. 如果z非常小，那么结果就越接近于0
               4. 从上面一张图中可以看到这个效果
         3. 所以当你实现logistic回归的时候，你要做的就是学习参数w和b，所以y^就变成了比较好的估计，对y=1的概率的比较好的估计，
3. 在对神经网络进行编程的时候，通常会把w和b分开，这里b对应一个拦截器，

来自为知笔记(Wiz)