树链剖分 （求LCA，第K祖先，轻重链剖分、长链剖分）

  2020/4/30   15:55

树链剖分是一种十分实用的树的方法，用来处理LCA等祖先问题，以及对一棵树上的节点进行批量修改、权值和查询等有奇效。

So， what is 树链剖分？

可以简单的理解为，将一棵树分成许多条不相交的链，每次我们只要得知链首，便可对该条链上所有的点用数据结构（like 线段树）进行相关操作 。

首先，介绍最常用的轻重链剖分。

明确最常用的轻重链概念：

重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；

轻儿子：父亲节点中除了重儿子以外的儿子；

重边：父亲结点和重儿子连成的边；

轻边：父亲节点和轻儿子连成的边；

重链：由多条重边连接而成的路径；

轻链：由多条轻边连接而成的路径；

如何求出以上的信息点呢？我们利用两次DFS。

第一次DFS，我们从根节点出发。用fa数组表示每个点的 爸爸， 用 siz 数组表示每个点子树的大小，son表示其重儿子，deth表示其相对于根节点的深度。

这部分其实挺好理解的：

（进入时记得初始化root的信息：   fa[root] = root, deth[root] = 1, siz[root] = 1）

(每次都先将siz初始化为1， 因为他们子树最小的情况就是只有他们自己）

void dfs1(int now, int father){
    int maxn = -;
    for(register int i = f[now]; i;i = t[i].next){
        int u = t[i].u, v = t[i].v;
        if(v != father){    /*无向图才加*/
            fa[v] = u; /*记录其父亲节点*/
            siz[v] = ;/*子树大小*/
            deth[v] = deth[u] +;/*记录深度*/
            dfs1(v, u);
            siz[u] += siz[v];
            if(siz[v] > maxn){  /*子树最大的才是重儿子*/
                maxv = siz[v];
                son[u] = v;
            }
        }
    }
    return ;
}

对于第二次DFS， 我们求出其链首和新编号，即数组 top 和 dfn。  为什么要求dfn值呢？因为我们将树剖分成了一条链，我们希望一条链上的点的编号是连续的，方便处理。因此重新记录dfn。

可是题目有时候的询问是问原编号呀？ 没事，我们记录一个 rev 数组，即新编号对应的原编号即可。当然，除了这些，有些特定的题目中我们可能还需要记录一些其他信息，比如对于每个节点，

其子树最大的编号maxw等。这些直接取max即可。

int dfs2(int now, int tp){
    top[now] = tp;
    maxw[now] = dfn[now] = ++id, rev[id] = now; /*记录信息*/
    if(!son[now])return maxw[now];
    dfs2(son[now], tp);      /*先遍历重儿子*/
    for(register int i = f[now]; i;i = t[i].next){
        int u = t[i].u, v = t[i].v;
        if(v != fa[u] && v != son[u]){
            maxw[now] = max(dfs2(v, v), maxw[now]);      /*开另外一条轻链，取最大的maxw*/
        }
    }
    return ;
}

 那么接下来进入正题：树链剖分的实际应用操作。

操作step1：  维护树的修改

洛谷P3384 轻重链剖分模板

不难想到，我们可以利用线段树维护每次操作。

为什么可以？ 因为上文我们已经提到，按照我们经过树链剖分所得到的新编号，是连续的（在同一条链上）。所以我们完全可以将树上的点想象成我们平常维护线段树时的原始数列。

对于链的修改，我们需要在上跳时（两个点一开始可能不在同一个树链上）不断对其进行区间维护。

对于子树的修改，我们则直接利用其新编号和子树 siz的大小，对区间进行修改（毕竟是可以直接算出来的吗）。

#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define isdigit(c) ((c)>='0'&&(c)<='9')

inline int read(){
    int x = , s = ;
    char c = getchar();
    while(!isdigit(c)){
        if(c == '-')s = -;
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x * s;
}

struct node{
    int v;
    int next;
} t[N << ];
int f[N];

int n, m, root, mod ,res = ;

struct tree{
    int add, w;
} e[N << ];

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){ v, f[u]}, f[u] = bian;
    t[++bian] = (node){u, f[v]}, f[v] = bian;
    return ;
}

int siz[N], son[N], fa[N] , deth[N];
int top[N], dfn[N], rev[N], id = ;
int a[N];
int w[N];

/*树链剖分板子------------*/ 

void dfs1(int now, int father){
    int maxn = -;
    for(int i = f[now]; i;i = t[i].next){
        int  v = t[i].v;
        if(v != fa[now]){
            deth[v] = deth[now] + ;
            siz[v] = , fa[v] = now;
            dfs1(v, now);
            siz[now] += siz[v];
            if(siz[v] > maxn){
                maxn = siz[v];
                son[now] = v;
            }
        }
    }
    return ;
}

void dfs2(int now, int tp){
    top[now] = tp, dfn[now] = ++id, rev[id] = now;
    w[id] = a[now];  /*把对应的权值转移*/
    if(!son[now])return ;
    dfs2(son[now], tp);
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        if(v != fa[now] && v != son[now]){
            dfs2(v, v);
        }
    }
    return ;
}
/*树链剖分完结-------------*/

/*线段 tree模板----------------*/

void build(int o, int l, int r){
    if(l == r){
        e[o].w = w[l] % mod;
        return ;
    }
    int mid = l + r >> ;
    build(o << , l, mid);
    build(o <<  | , mid + , r);
    e[o].w = (e[o << ].w + e[o <<  | ].w + mod) % mod;
    return ;
}

inline void pushdown(int o, int len){
    e[o << ].add  = (e[o << ].add + e[o].add) % mod;
    e[o <<  | ].add = (e[o <<  | ].add + e[o].add) % mod;
    e[o << ].w = (e[o << ].w + e[o].add * (len - (len >> ))) % mod;
    e[o <<  | ].w = (e[o <<  | ].w + e[o].add * (len >> )) % mod;
    e[o].add = ;
    return ;
}

void update(int o, int l, int r, int in, int end, int k){
    if(l > end || r < in)return;
    if(l >= in && r <= end){
        e[o].add = (e[o].add + k) % mod;
        e[o].w = (e[o].w + k * (r - l + )) % mod;  /*记得更新w*/
        return ;
    }
    pushdown(o, r - l + );
    int mid = l + r >> ;
    if(l <= mid)update(o << , l, mid, in, end, k);
    if(r > mid)update(o <<  | , mid + , r, in, end , k);
    e[o].w = (e[o << ].w + e[o <<  | ].w) % mod;
    return ;
}

int query(int o, int l, int r, int in, int end){
    if(l > end || r < in)return ;
    if(l >= in && r <= end){
        return e[o].w;
    }
    int mid = l + r >> ;
    pushdown(o, r - l + );
    return (query(o << , l, mid, in, end) + query(o <<  | , mid + , r, in, end)) % mod;
}
/*线段tree  完结---------*/

/*两边结合部分*/
int ask_lian(int x, int y){
    int ans = ;
    while(top[x] != top[y]){  /*还不在同一条链上的时候*/
        if(deth[top[x]] < deth[top[y]]) swap(x, y);
        ans += query(, , n, dfn[top[x]], dfn[x]);
        x = fa[top[x]];
    }
    res = ;
    if(deth[x] > deth[y]) swap(x, y);
    ans += query(, , n, dfn[x], dfn[y]);
    return ans % mod;
}

void update_lian(int x, int y, int k){
    k %= mod;
    while(top[x] != top[y]){
        if(deth[top[x]] < deth[top[y]]) swap(x, y); /*让x更深*/
        update(, , n, dfn[top[x]], dfn[x], k);
        x = fa[top[x]];
    }
    if(deth[x] > deth[y]) swap(x, y); /*让x更浅*/
    update(, , n, dfn[x], dfn[y], k);
    return ;
}

void update_tree(int x, int k){
    update(, , n, dfn[x], dfn[x] + siz[x] - , k);
    return ;
}

int ask_tree(int x){
    return query(, , n, dfn[x], dfn[x] + siz[x] - ) % mod;  /*右端点就是dfn + siz - 1*/
}
/*更新区域完结---------------*/

int main(){
//    freopen("hh.txt", "r", stdin);
    n = read(), m = read(), root = read(), mod = read();
    for(int i = ;i <= n; i++)a[i] = read();
    for(int i = ;i < n; i++){
        int x = read(), y = read();
        add(x, y);
    }
    deth[root] = ;
    fa[root] = root;
    siz[root] = ;
    dfs1(root, root);
    dfs2(root, root);
    build(, , n);
    while(m--){
        int flag = read();
        if(flag == ){
            int x = read(), y = read(), k = read();
            update_lian(x, y, k);
        }
        else if(flag == ){
            int x = read(), y = read();
            printf("%d\n", ask_lian(x, y));
        }
        else if(flag == ){
            int x = read(), k = read();
            update_tree(x, k);
        }
        else if(flag == ){
            int x = read();
            printf("%d\n", ask_tree(x));
        }
    }
    return ;
}

here

友情tips：

这个模板或许思路很简单，但是在计算过程中有一个很重要的思路细节：在对链进行修改的时候，两个目标端不一定在同一链上。因此要先对其进行上跳，并且对途中经过的点也进行修改（毕竟也在我们的目标区间中）、

 再来一道例题：

SDOi 2014（山东省2014省选）  旅行 洛谷P3313

对比板子题，这题要稍微难一丢丢。

首先看完题面，进行翻译，其实就是树链剖分+线段树的板子题。

对于每一个宗教，我们都开一个线段树维护。

什么？空间开不下？

没事，我们来动态开点。

线段树动态开点浅谈：

1、参考dalao博客

2、如此考虑：

很多时候，我们的一棵线段树，如果我们建n << 2个节点，实际上我们是浪费了的。因此，我们就换一种思路：需要它，我们才开它。

那么，由于有许许多多的东东共用内存，我们也就不能用什么 o << 1和 o << 1 | 1了，而是全部改用 lson和rson记录儿子编号。

同时，在每次使用前，我们改节点要进行删除操作，清空原节点信息，以免影响。

可是，如何保证lson和rson的正确性，或者说，如何获得他们呢？？  

神的标识符：  "&"。

每次开新节点时，我们&标识符就可以对lson和rson进行更新了！

如果看不懂的话，尝试着结合代码吧。

#include <bits/stdc++.h>
using namespace std;
#define N 1000100
/*树链剖分+线段树动态开点板子*/
inline int read(){
    int x = ;
    char c = getchar();
    while(!isdigit(c)){
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x;
}

struct node{
    int v, next;
}t[N << ];
int f[N];
int n, q;

int siz[N], son[N], fa[N], deth[N];
int top[N], dfn[N], rev[N], id = ;
int w[N], c[N], T[N];  /*T记录对应的线段树的根节点*/

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){v, f[u]}, f[u] = bian;
    t[++bian] = (node){u, f[v]}, f[v] = bian;
    return;
}

void dfs1(int u, int father){
    deth[u] = deth[father] + ;
    fa[u] = father;
    siz[u] = ;
    int maxn = -;
    for(int i = f[u]; i;i = t[i].next){
        int v = t[i].v;
        if(v != fa[u]){
            dfs1(v, u);
            siz[u] += siz[v];
            if(siz[v] > maxn){
                son[u] = v;
                maxn = siz[v];
            }
        }
    }
    return ;
}

void dfs2(int u, int rt){
    dfn[u] = ++id, rev[id] = u;
    top[u] = rt;
    if(!son[u]) return ;
    dfs2(son[u], rt);
    for(int i = f[u]; i;i = t[i].next){
        int v = t[i].v;
        if(v != fa[u] && v != son[u]){
            dfs2(v, v);
        }
    }
    return ;
}

struct tree{
    int val, w;  // max num  and you know
    int lson, rson;
} e[N << ];
int cnt = ;

inline void pushup(int o){
    e[o].val = max(e[e[o].lson].val, e[e[o].rson].val);
    e[o].w = e[e[o].lson].w + e[e[o].rson].w;
    return ;
}

void build(int& o, int l, int r, int x, int k){
    if(!o) o = ++cnt;  /*如果没有它，我们就创造它！！*/
    if(l > x || r < x)return ;
    if(l == r){
        e[o].val = e[o].w = k;
        return ;
    }
    int mid = l + r >> ;
    build(e[o].lson, l, mid, x, k);
    build(e[o].rson, mid + , r, x, k);
    pushup(o);
    return ;
}

void del(int& o, int l, int r, int x ){
    if(!o) return ;
    if(l > x || r < x) return ;
    if(l == r){
        e[o].val = e[o].w = ; //delete the point
        return ;
    }
    int mid = l + r >> ;
    del(e[o].lson, l, mid, x);
    del(e[o].rson, mid + , r, x);
    pushup(o); // do not forget to update the data of the tree
    return ;
}    

int query_sum(int& o, int l, int r, int in, int end){
    if(!o) return ;
    if(r < in || l > end) return ;
    if(l >= in && r <= end){
        return e[o].w;
    }
    int mid = l + r >> ;
    return query_sum(e[o].lson, l, mid, in, end) + query_sum(e[o].rson, mid + , r, in, end);
}

int query_max(int& o, int l, int r, int in, int end){
    if(!o) return ;
    if(l > end || r < in)return ;
    if(l >= in && end >= r){
        return e[o].val;
    }
    int mid = l + r >> ;
    return max(query_max(e[o].lson, l, mid, in, end), query_max(e[o].rson, mid + , r, in, end));
}

int ask_he(int x, int y){
    int k = c[x];
    int ans = ;
    while(top[x] != top[y]){
        if(deth[top[x]] < deth[top[y]]) swap(x, y);
        ans += query_sum(T[k], , n, dfn[top[x]], dfn[x]);
        x = fa[top[x]];
    }
    if(deth[x] > deth[y]) swap(x, y);
    ans += query_sum(T[k], , n, dfn[x], dfn[y]);
    return ans;
}

int ask_maxn(int x, int y){
    int ans = -(~ >> );
    int k = c[x];
    while(top[x] != top[y]){
        if(deth[top[x]] < deth[top[y]]) swap(x, y);
        ans = max(ans, query_max(T[k], , n, dfn[top[x]], dfn[x]));
        x = fa[top[x]];
    }
    if(deth[x] > deth[y]) swap(x, y);
    ans = max(ans, query_max(T[k], , n, dfn[x], dfn[y]));
    return ans;
}

int main(){
//    freopen("hh.txt", "r", stdin);
    n = read(), q = read();
    for(int i = ;i <= n; i++){
        w[i] = read(), c[i] = read();
    }
    for(int i = ;i < n; i++){
        int x = read(), y = read();
        add(x, y);
    }
    dfs1(, );  dfs2(, );
    for(int i = ;i <= n; i++){
        build(T[c[rev[i]]], , n, i, w[rev[i]]);
    }
    char temp[];
    while(q--){
        scanf("%s", temp);
        int x, k;
        if(temp[] == 'C'){
            x = read(), k = read();
            del(T[c[x]], , n, dfn[x]);
            c[x] = k;
            build(T[c[x]], , n, dfn[x], w[x]);
        }
        else if(temp[] == 'W'){
            x = read(), k = read();
            del(T[c[x]], , n, dfn[x]);
            w[x] = k;
            build(T[c[x]], , n, dfn[x], w[x]);
        }
        else if(temp[] == 'S'){
            int x = read(), y = read();
            printf("%d\n", ask_he(x, y));
        }
        else if(temp[] == 'M'){
            int x = read(), y = read();
            printf("%d\n", ask_maxn(x, y));
        }
    }
    return ;
}

here

upd:    还有的很好的树剖练手题（刷经验题）

  

P2590 [ZJOI2008]树的统计

 树的统计代码：

#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define ll long long
#define isdigit(c) ((c)>='0'&&(c)<='9')

inline void swap(int& a, int &b){
    a ^= b ^= a ^= b;
    return;
}

inline int max(int a, int b){
    return a > b ? a : b;
}

inline ll read(){
    ll x = , s = ;
    char c = getchar();
    while(!isdigit(c)){
        if(c == '-')s = -;
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x * s;
} 

struct node{
    int v;
    int next;
} t[N << ];
int f[N];

int siz[N], top[N],deth[N], son[N], fa[N];
int dfn[N], id = , rev[N];
int a[N];

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){v, f[u]}, f[u] = bian;
    t[++bian] = (node){u, f[v]}, f[v] = bian;
    return ;
}

void dfs1(int now, int father){
    deth[now] = deth[father] + ;
    fa[now] = father;
    siz[now] = ;
    int maxn = -;
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        if(v != fa[now]){
            dfs1(v, now);
            siz[now] += siz[v];
            if(siz[v] >= maxn){
                son[now] = v;
                maxn = siz[v];
            }
        }
    }
    return ;
}

void dfs2(int now, int tp){
    top[now] = tp;
    dfn[now] = ++id;
    rev[id] = now;
    if(!son[now]) return ;
    dfs2(son[now], tp);
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        if(v != fa[now] && v != son[now]){
            dfs2(v, v);
        }
    }
    return ;
}

struct tree{
    int w, maxn;
} e[N << ];
int n;

inline void pushup(int o){
    e[o].w = e[o << ].w + e[o <<  | ].w;
    e[o].maxn = max(e[o << ].maxn, e[o <<  | ].maxn);
    return ;
}

void build(int o, int l, int r){
    if(l == r){
        e[o].w = e[o].maxn = a[rev[l]];
        return ;
    }
    int mid = l + r >> ;
    build(o << , l, mid);
    build(o <<  | , mid + , r);
    pushup(o);
    return ;
}

void update(int o, int l, int r, int x, int k){
    if(l > x || r < x) return;
    if(l == r){
        e[o].w = e[o].maxn = k;
        return ;
    }
    int mid = l + r >> ;
    update(o << , l, mid, x, k);
    update(o <<  | , mid + , r, x, k);
    pushup(o);
    return ;
}

ll query(int o, int l, int r, int in, int end){
    if(l > end || r < in) return ;
    if(l >= in && r <= end){
        return e[o].w;
    }
    int mid = l + r >> ;
    return query(o << , l, mid, in, end) + query(o <<  | , mid + , r, in, end);
}

ll query_max(int o, int l, int r, int in, int end){
    if(l > end || r < in) return -;
    if(l >= in && r <= end){
        return e[o].maxn;
    }
    int mid = l + r >> ;
    return max(query_max(o << , l, mid ,in, end) , query_max(o <<  | , mid + , r, in, end));
}

ll ask_he(int x, int y){
    ll ans = ;
    while(top[x] != top[y]){
        if(deth[top[x]] < deth[top[y]]) swap(x, y);
        ans += query(, , n, dfn[top[x]], dfn[x]);
        x = fa[top[x]];
    }
    if(deth[x] > deth[y]) swap(x, y);
    ans += query(, , n, dfn[x], dfn[y]);
    return ans;
}

ll ask_max(int x, int y){
    ll ans = -;
    while(top[x] != top[y]){
        if(deth[top[x]] < deth[top[y]]) swap(x, y);
        ans = max(ans, query_max(, , n, dfn[top[x]], dfn[x]));
        x = fa[top[x]];
    }

    if(deth[x] > deth[y]) swap(x, y);
    ans = max(ans, query_max(, , n, dfn[x], dfn[y]));
    return ans;
}

int main(){
//    freopen("hh.txt", "r", stdin);
    n = read();
    for(int i = ;i < n; i++){
        int a = read(), b = read();
        add(a, b);
    }
    for(int i = ;i <= n; i++) a[i] = read();
    dfs1(, );
    dfs2(,);
    build(, , n);
    int q = read();
    char ch[];
    while(q--){
        scanf("%s", ch);
        if(ch[] == 'H'){
            int x = read(), k = read();
            update(, , n, dfn[x], k);
        }
        if(ch[] == 'S'){
            int l = read(), r = read();
            printf("%d\n", ask_he(l, r));
        }
        if(ch[] == 'M'){
            int x = read(), y = read();
            printf("%d\n", ask_max(x, y));
        }
    }
    return ;
}

SDOI 2011  染色 

操作step2： 求LCA

洛谷最近公共祖先AC通道！

对于求LCA的问题，目前主流有三种求法：  倍增、tarjan，还有一个就是我们的树剖。

对比下来，倍增常数较大，而且写起来麻烦（至少蒟蒻的我是不喜欢倍增）

tarjan算法在时间复杂度上十分强大，只需要O（N）预处理（求LCA） + O(1) 的询问。

但是，

tarjan必须提前知道所有的询问，然后一次性求出。也就是说，tarjan强制离线！

于是，求LCA的第三大方法，树剖，横空出世。

根据dalao的证明，树剖和倍增复杂度都是O（NlogN），但是，树剖的常数要比倍增小。（主要原因是好写）

所以，蒟蒻的我便选择树剖求LCA吧！

树剖完成后的操作：

对于每个询问，我们选择上跳，直到两个点在同一链上，然后深度浅（在上面）的那个点自然就是其LCA了。

对于该方法的正确性，见大佬博客 以下证明：（为什么用树剖求LCA的人辣么少）

       洛谷拉的图，侵删

首先根据上面的轻重链定义，我们可以发现，树链剖分后，我们得到的图应该是这样的：

                                                                                 

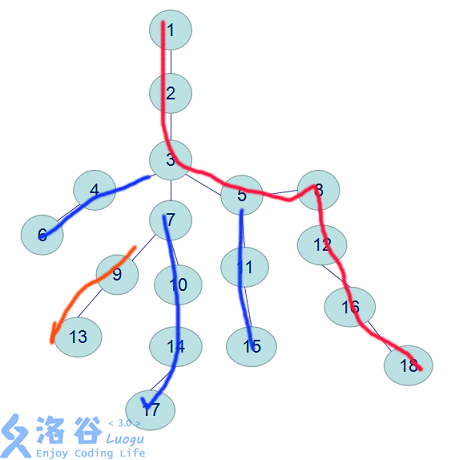
其中最长的那条红红的东东就是我们所说的重链了（1 ~ 18），轻链则是剩下的那些短短的。

那么，如果我们每次上跳，可以手摸出来，最坏的情况，两个点的LCA也一定会在一条链上出现。于是，我们每次只用在上跳时判断，两个点的top是否一样（每个点只会在一条链上出现，因此链首就是该链的颜值代表）。如果不一样，我们继续上跳。如果一样，深度浅的那个就是我们要的LCA。

有关上跳操作的tips:   因为每次我们都要跳到另外一条链，所以当然是跳这条链首的爸爸啦！！可以自行手摸体会。

code：

#include<bits/stdc++.h>
using namespace std;
#define N 1000100
#define isdigit(c) ((c)>='0'&&(c)<='9')

inline int read(){
    int x = , s = ;
    char c = getchar();
    while(!isdigit(c)){
        if(c == '-')s = -;
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x * s;
}

struct node{
    int u, v;
    int next;
} t[N];
int f[N];
int fa[N], siz[N], deth[N], son[N], top[N];
int dfn[N], rev[N], id = ;
int maxw[N]; /*取得子树上最大的编号*/

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){u, v, f[u]};
    f[u] = bian;
    t[++bian] = (node){v, u, f[v]};
    f[v] = bian;
    return ;
}

void dfs1(int now, int father){
    int maxn = -;
    for(register int i = f[now]; i;i = t[i].next){
        int u = t[i].u, v = t[i].v;
        if(v != father){    /*无向图才加*/
            fa[v] = u; /*记录其父亲节点*/
            siz[v] = ;/*子树大小*/
            deth[v] = deth[u] +;/*记录深度*/
            dfs1(v, u);
            siz[u] += siz[v];
            if(siz[v] > maxn){  /*子树最大的才是重儿子*/
                maxn = siz[v];
                son[u] = v;
            }
        }
    }
    return ;
}

void dfs2(int now, int tp){
    top[now] = tp;
    dfn[now] = ++id, rev[id] = now; /*记录信息*/
    if(!son[now])return ;
    dfs2(son[now], tp);      /*先遍历重儿子*/
    for(register int i = f[now]; i;i = t[i].next){
        int u = t[i].u, v = t[i].v;
        if(v != fa[u] && v != son[u]){
            dfs2(v, v);
        }
    }
    return ;
}

inline void LCA_prepare(int s){
    fa[s] = s;
    siz[s] = ;
    deth[s] = ;
    dfs1(s,s);
    dfs2(s, s);
    return ;
}

int Answer(int x, int y){
    while(top[x] != top[y]){
        if(deth[top[y]] >= deth[top[x]]){
            y = fa[top[y]]; /*一定要跳到链首的父亲节点，不然还在同一条链上*/
        }
        else x = fa[top[x]];
    }
    return deth[x] <= deth[y] ? x : y; /*lca肯定是深度比较小（在上面的）的那个*/
} 

int main(){
    int n = read(), m = read(), root = read();
    for(int i = ; i < n; i++){
        int x = read(), y = read();
        add(x, y);
    }
    LCA_prepare(root);
    while(m--){
        int x = read(), y = read();
        printf("%d\n", Answer(x, y));
    }
    return ;
}

Here is the code

操作step3:  长链剖分求K级祖先

洛谷AC通道

首先，这是一道长链剖分的板子题，题目背景也说了，是用来测试长链剖分的。

于是，我们先想想怎么用轻重链剖分做这道题。（滑稽）

查看方法1：我发的题解

查看方法2：洛谷题解

其实思路和求LCA差不多，只不过在上跳时我们特别的计算一下就好了。。。

轻重链剖分歪解：

#include <bits/stdc++.h>
using namespace std;
#define N 1000100
#define ll long long
#define ui unsigned int
ui S;

/*正解应该写长链剖分，但这里用的重链剖分*/

inline ui get(ui x) {
    x ^= x << ;
    x ^= x >> ;
    x ^= x << ;
    return S = x;
} /*题目给的*/

inline int read(){
    int x = , s = ;
    char c = getchar();
    while(!isdigit(c)){
        if(c == '-')s = -;
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x * s;
}

int root;
int dfn[N], rev[N], id = ;
int fa[N], son[N];
int deth[N], siz[N], top[N];

struct node{
    int u, v;
    int next;
} t[N << ];
int f[N];

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){u, v, f[u]};
    f[u] = bian;
    t[++bian] = (node){v, u, f[v]};
    f[v] = bian;
    return ;
}

/*两次dfs*/
void dfs1(int now){
    siz[now] = ;
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v, u = t[i].u;
        if(v != fa[u]){
            fa[v] = u;
            deth[v] = deth[u] + ;
            dfs1(v);
            siz[u] += siz[v];
            if(siz[son[u]] < siz[v]){
                son[u] = v;
            }
        }
    }
    return ;
}

void dfs2(int now){
    dfn[now] = ++id;
    rev[id] = now;
    if(!son[now])return ;
    top[son[now]] = top[now];
    dfs2(son[now]);
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v, u = t[i].u;
        if(v != son[u] && v != fa[u]){
            top[v] = v;
            dfs2(v);
        }
    }
    return ;
}

int jump(int x, int k) {
    int temp = deth[x] - k;
    while (deth[top[x]] > temp) x = fa[top[x]];
    temp = deth[x] - temp;
    return rev[dfn[x] - temp];
}

int main(){
//  freopen("hh.txt", "r", stdin);
    int n = read(), q = read(); cin >> S;
    for(int i = ;i <= n; i++){
        fa[i] = read();
        if(!fa[i]) root = i;
        else add(fa[i], i);
    }
    deth[root] = ; /*不要忘记初始化哦*/
    dfs1(root);
    top[root] = root;
    dfs2(root);
    ll ltans = , ans = ;  /*不开long long见祖宗*/
    for(int i = ;i <= q; i++){
        int x = (get(S) ^ ltans) % n + ;
        int k = (get(S) ^ ltans) % deth[x];
        ltans = jump(x, k);
        ans ^= (ll)i * ltans;
    }
    printf("%lld\n", ans);
    return ;
}

歪解，勿学

 那么正解长链剖分呢？？ 还没学，不会。。。。（以后更新）

upd on 2020.5.15

长链剖分补锅！！

首先，从名字来看，长链剖分和轻重链剖分最大的不同，就是它们的名字不一样，就是它们的链不一样。

与轻重链相比，长链剖分的大部分定义都一样，唯独需要我们修改的，就是其对于儿子的定义：

在这里，我们求得不再是重儿子，而是“长儿子”。

什么是长儿子？  类比重儿子。

重儿子是指子树最大的，而“长儿子”就是指其深度最深的的儿子。也可以理解为，其最长的儿子。

。。。看起来好像有点解释不清。。。

没事，上图：

                                                       

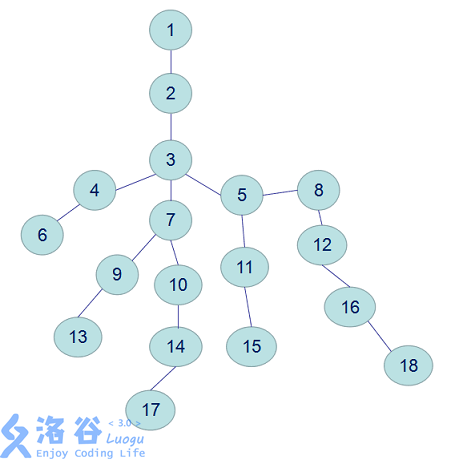
很不幸，在上面这张图中，我们3号节点的“长儿子”依然是5,   5号节点的长儿子依然是8.

但是，如果遇到这种情况呢：

我们的11号节点上接了666个点。

如果按照重儿子的定义，那么我们的5号节点的重儿子就要变成11了，因为人家有 668这么大。

而按照“长儿子”的定义，我们五号节点的长儿子依然还是8.因为18号节点的深度依然大于11、15等节点。

知道了定义之后，如何求呢？

 直接上代码：（倍增后面再说）

void dfs1(int now){
    int maxn = -;
    for(int i = ;i <= ; i++)
        fa[now][i] = fa[fa[now][i-]][i-]; /*预处理倍增*/
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        deth[v] = len[v] = deth[now] + ;
        dfs1(v);
        len[now] = max(len[now], len[v]);
        if(len[v] > maxn){
            son[now] = v;
            maxn = len[v];
        }
    }
    return ;
}

对于dfs1，我们可以手摸出来：  对于链的长度（从链首到当前节点）len[i]，len[i] = deth[u] + 1, 所以这里不再多做解释。中间记得取len的最大值就ok了。

void dfs2(int now, int tp){
    dfn[now] = ++id, rev[id] = now;
    dev[id] = tp;  /*从id反向查询 top和真实编号*/
    if(!son[now])return ;
    if(son[now]) {
        top[son[now]] = top[now];   /*这里和重链剖分处理top的方法不一样（注意dfs2中填入的）*/
        dfs2(son[now], fa[tp][]);
    }
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        if(v != son[now]){
            top[v] = v;
            dfs2(v, v);
        }
    }
    return ;
} 

对于dfs2,不同点就是，我们需要多记录一些东西，用于之后的查询（当然不同的题可能不一样），以及对于top数组记录的方法不同。

首先，rev即查回自己原始编号，（之后用于向下查），dev为当前的tp（用于向上查）

这里，我们长链剖分一定要将tp改成fa[tp]的上一个点，至于为何，自己手摸。

也正是由于这一不同，我们需要注意对top数组维护的方法。（top数组定义跟以前一样）。

 重头戏开始了！

我们求出了长链之后，怎么查询K级祖先呢？

当然是选择倍增啦！

为了使查询更快，我们进行倍增的预处理，即求出每个点的2ⁿ的祖先。

然后，对于 i ∈ [1, n], 我们求出二进制下最高位 Log[i]。

然后，对于询问 (x, k)  我们每次直接把x跳到 Log[k]级的位置。 假设如此操作之后，我们距离目标还剩下 k' 级，显然，k' < 2^h[k]次方。

那么，x目前所在的长链的长度一定 > k'。

接下来就好办了。

我们直接把x跳到链顶部，然后判断一下，k'是在我们上面还是下面（即正负）。然后直接  + k'  或者  - k'向上查或者向下查就好了。

第K祖先代码：

#include <bits/stdc++.h>
using namespace std;
#define N 6666666
#define isdigit(c) ((c)>='0'&&(c)<='9')
/*长链剖分*/

#define ui unsigned int
ui s;
inline ui get(ui x) {
    x ^= x << ;
    x ^= x >> ;
    x ^= x << ;
    return s = x;
}
#undef ui

inline int read(){
    int x = ,s = ;
    char c = getchar();
    while(!isdigit(c)){
        if(c == '-')s = -;
        c = getchar();
    }
    while(isdigit(c)){
        x = (x << ) + (x << ) + (c ^ '');
        c = getchar();
    }
    return x * s;
}

struct node{
    int u, v;
    int next;
} t[N];
int f[N];

int top[N], son[N], deth[N];
int dfn[N], rev[N], id = ;
int len[N], dev[N];
int fa[N][];
int Log[N];

int bian = ;
inline void add(int u, int v){
    t[++bian] = (node){u, v, f[u]}, f[u] = bian;
    return ;
}

void dfs1(int now){
    int maxn = -;
    for(int i = ;i <= ; i++)
        fa[now][i] = fa[fa[now][i-]][i-]; /*预处理倍增*/
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        deth[v] = len[v] = deth[now] + ;
        dfs1(v);
        len[now] = max(len[now], len[v]);
        if(len[v] > maxn){
            son[now] = v;
            maxn = len[v];
        }
    }
    return ;
}

void dfs2(int now, int tp){
    dfn[now] = ++id, rev[id] = now;
    dev[id] = tp;  /*从id反向查询 top和真实编号*/
    if(!son[now])return ;
    if(son[now]) {
        top[son[now]] = top[now];   /*这里和重链剖分处理top的方法不一样（注意dfs2中填入的）*/
        dfs2(son[now], fa[tp][]);
    }
    for(int i = f[now]; i;i = t[i].next){
        int v = t[i].v;
        if(v != son[now]){
            top[v] = v;
            dfs2(v, v);
        }
    }
    return ;
} 

inline int ask(register int x, register int k){
    if(!k) return x;
    x = fa[x][Log[k]];  /*先直接跳到最上面*/
    k -= ( << Log[k]);
    k -= deth[x] - deth[top[x]];  /*然后下跳*/
    x = top[x];
    if(k >= ) return dev[dfn[x] + k];
    else return rev[dfn[x] - k];
}

#define ll long long
int main(){
    register int n = read(), q = read(), root = ;cin >> s;
    for(int i = ;i <= n; i++){
        fa[i][] = read();
        if(fa[i][] == ) root = i;
        else {
            add(fa[i][], i);
        }
    }
    Log[] = -;
    for(int i = ;i <= n; ++i)
        Log[i] = Log[i >> ] + ;
    /*预处理出所有的Log*/
    deth[root] = ;
    dfs1(root);
    top[root] = root;
    dfs2(root, root);
    int lstans;
    ll ans = ;
    for(int i = ;i <= q;i++){
        register int x = (get(s) ^ lstans) % n + , k = (get(s) ^ lstans) % deth[x];
        lstans = ask(x, k);
        ans ^= (ll)i * lstans;
    }
    printf("%lld\n", ans);
    return ;
}
#undef ll

 参考资料：  大佬博客     大佬2博客

它真的完了。。。