A - Investment

A - Investment

John never knew he had a grand-uncle, until he received the notary’s letter. He learned that his late grand-uncle had gathered a lot of money, somewhere in South-America, and that John was the only inheritor.

John did not need that much money for the moment. But he realized that it would be a good idea to store this capital in a safe place, and have it grow until he decided to retire. The bank convinced him that a certain kind of bond was interesting for him.

This kind of bond has a fixed value, and gives a fixed amount of yearly interest, payed to the owner at the end of each year. The bond has no fixed term. Bonds are available in different sizes. The larger ones usually give a better interest. Soon John realized that the optimal set of bonds to buy was not trivial to figure out. Moreover, after a few years his capital would have grown, and the schedule had to be re-evaluated.

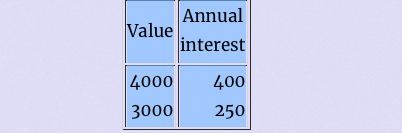
Assume the following bonds are available:



With a capital of e10 000 one could buy two bonds of $4 000, giving a yearly interest of $800. Buying two bonds of $3 000, and one of $4 000 is a better idea, as it gives a yearly interest of $900. After two years the capital has grown to $11 800, and it makes sense to sell a $3 000 one and buy a $4 000 one, so the annual interest grows to $1 050. This is where this story grows unlikely: the bank does not charge for buying and selling bonds. Next year the total sum is $12 850, which allows for three times $4 000, giving a yearly interest of $1 200.

Here is your problem: given an amount to begin with, a number of years, and a set of bonds with their values and interests, find out how big the amount may grow in the given period, using the best schedule for buying and selling bonds.

Input

The first line contains a single positive integer N which is the number of test cases. The test cases follow.

The first line of a test case contains two positive integers: the amount to start with (at most $1 000 000), and the number of years the capital may grow (at most 40).

The following line contains a single number: the number d (1 <= d <= 10) of available bonds.

The next d lines each contain the description of a bond. The description of a bond consists of two positive integers: the value of the bond, and the yearly interest for that bond. The value of a bond is always a multiple of $1 000. The interest of a bond is never more than 10% of its value.

Output

For each test case, output – on a separate line – the capital at the end of the period, after an optimal schedule of buying and selling.

Sample Input

1
10000 4
2
4000 400
3000 250

Sample Output
14050

思路如下

这一题是一个完全背包的模型，在做题的时候我们需要注意一些地方，我 手中的总钱数money在每一过一年是会增加的（因为股票的利润），所以我们的 前变为：money += f[money/1000]（该年的利润）;其次这一个题的数据范围非常大，而数组是不可能开这么大的，但是这一题又说了 股票的价格是以1000的倍数，手中的钱money也是1000倍数 ，所以我们可以同时 讲 每支股票的价格 与手中的金钱 同除以1000，这样我们开的数组就足放的下所有数据了

题解如下

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

struct Node
{
    int pri;
    int val;
};
Node node[100];

int main()
{
    int q;
    //cin>>q;
    scanf("%d",&q);
    while(q--)
    {
        int money,year,spci; 		//spci 为股票的种类
        //cin>>money>>year>>spci;
        scanf("%d%d%d",&money,&year,&spci);
        for(int i = 1;i <= spci;i ++)
        {
            int temp;
            //cin>>temp>>node[i].val;
            scanf("%d%d",&temp,&node[i].val);
            node[i].pri = temp/1000;	//除以1000缩小范围
        }
        while(year--)
        {
            int f[100005] = {0};		//状态转移方程
            for(int i = 1;i <= spci;i ++)
                for(int mon = node[i].pri;mon <= money/1000;mon ++)
                    f[mon] = max(f[mon],f[mon - node[i].pri ] + node[i].val);
            money += f[money/1000];
        }
        cout<<money<<endl;
    }
    return 0;
}