java实现第五届蓝桥杯六角幻方

六角幻方

里面的*在编写的时候会自动编译成线，这里就用代码的格式把题目弄过来

 把 1 2 3 ... 19 共19个整数排列成六角形状，如下：

    * * *
   * * * *
  * * * * *
   * * * *
    * * *

    要求每个直线上的数字之和必须相等。共有15条直线哦！

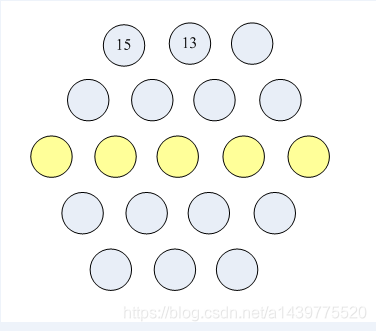
    再给点线索吧！我们预先填好了2个数字，第一行的头两个数字是：15 13，参见图【p1.png】，黄色一行为所求。

    请你填写出中间一行的5个数字。数字间用空格分开。

    这是一行用空格分开的整数，请通过浏览器提交答案，不要填写任何多余的内容（比如说明性的文字等）

9 6 5 2 16

public class Main {
    public static boolean[] used = new boolean[20];

    public void swap(int[] A, int i, int j) {
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }

    public boolean check(int[] A, int step) {
        int sum = A[0] + A[1] + A[2];
        if(step >= 7) {
            if(A[3] + A[4] + A[5] + A[6] != sum)
                return false;
        }
        if(step >= 8)
            if(A[0] + A[3] + A[7] != sum)
                return false;
        if(step >= 12) {
            if(A[7] + A[8] + A[9] + A[10] + A[11] != sum)
                return false;
            if(A[2] + A[6] + A[11] != sum)
                return false;
        }
        if(step >= 13)
            if(A[1] + A[4] + A[8] + A[12] != sum)
                return false;
        if(step >= 16) {
            if(A[12] + A[13] + A[14] + A[15] != sum)
                return false;
            if(A[1] + A[5] + A[10] + A[15] != sum)
                return false;
        }
        if(step >= 17) {
            if(A[2] + A[5] + A[9] + A[13] + A[16] != sum || A[7]+A[12]+A[16] != sum)
                return false;
        }
        if(step >= 18)
            if(A[3] + A[8] + A[13] + A[17] != sum || A[6] + A[10] + A[14] + A[17] != sum)
                return false;
        if(step >= 19) {
            if(A[0]+A[4]+A[9]+A[14]+A[18] != sum || A[16] + A[17] + A[18] != sum || A[11] + A[15] + A[18] != sum)
                return false;
        }
        return true;
    }

    public void dfs(int[] A, int step) {
        if(check(A, step) == false)
            return;
        if(step == 19) {
            for(int i = 0;i < A.length;i++)
                System.out.print(A[i]+" ");
            System.out.println();
            return;
        }
        for(int i = 1;i <= 19;i++) {
            if(used[i] == false) {
                used[i] = true;
                A[step] = i;
                dfs(A, step + 1);
                used[i] = false;
            }
        }

    }

    public static void main(String[] args) {
        Main test = new Main();
        int[] A = new int[19];
        A[0] = 15;
        A[1] = 13;
        A[2] = 10;
        used[15] = true;
        used[13] = true;
        used[10] = true;
        test.dfs(A, 3);
    }
}