锋利的JQuery —— 选择器
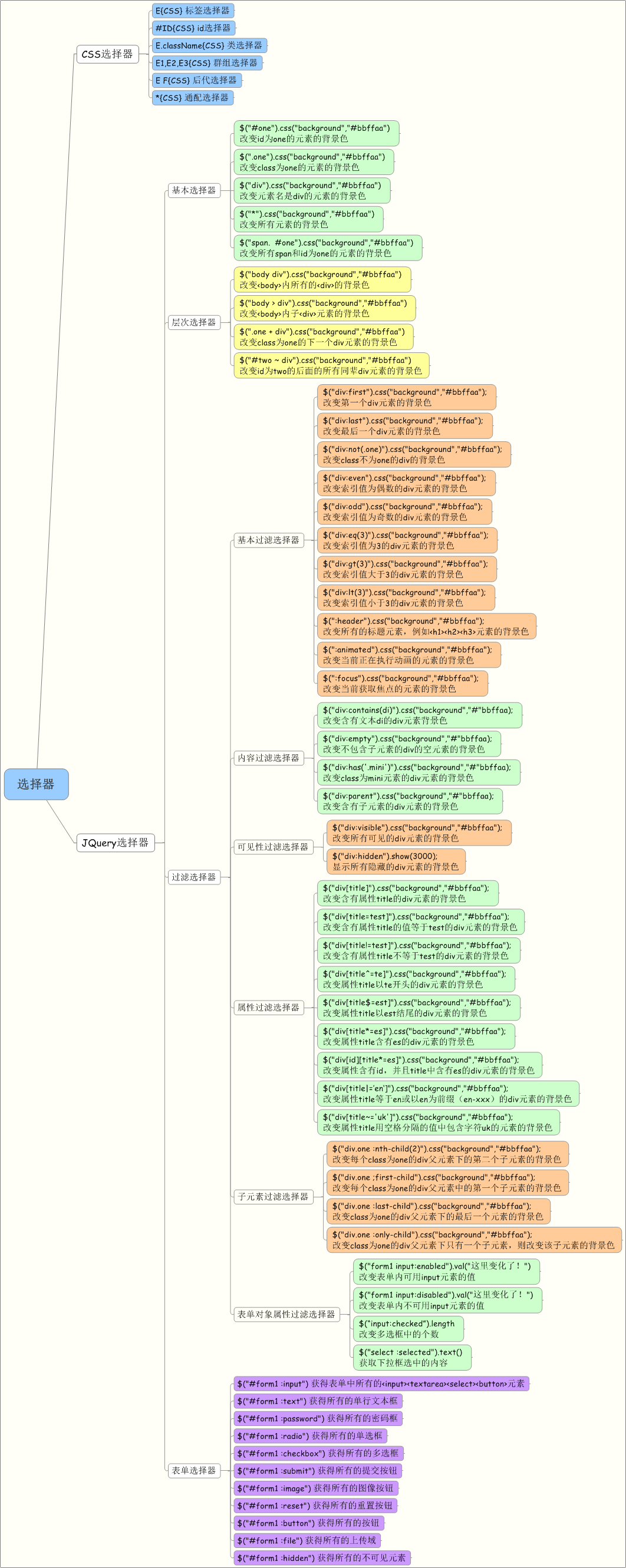
锋利的JQuery —— 选择器的更多相关文章
- 锋利的jQuery读书笔记---选择器
前段时间入手了锋利的jQuery(第二版),想着加强下自己的js能力,可前段时间一只在熟悉Spring和Hibernate.最近抽时间开始读这本书了,随便也做了些记录. 读书的过程是边看边代码测试,所 ...
- 《锋利的JQuery》读书要点笔记1——认识JQuery&&选择器
<锋利的jQuery>源码下载,包括了这本书中全部代码以及用到的CSS文件 第一章 认识jQuery jQuery是个Js库.首先该明确的一点是:在jQuery库中$就是jQuery的一个 ...
- 《锋利的jQuery(第2版)》笔记-第2章-jQuery选择器
选择器是jQuery的根基,在jQuery中,对事件处理.遍历DOM和Ajax操作都依赖于选择器.熟练使用选择器,不仅可以简化代码,而且可以达到事半功倍的效果. 2.1 jQuery选择器是什么 1. ...
- jQuery选择器和DOM操作——《锋利的jQuery》(第2版)读书笔记1
第1章 认识jQuery jQuery有以下优势: 轻量级: 强大的选择器: 出色的DOM操作的封装: 可靠的事件处理机制: 完善的Ajax: 不污染顶级变量: 出色的浏览器兼容性: 链式操作方式: ...
- 【学习笔记】锋利的jQuery(一)选择器
一.要点阐述 1,jQuery创建于2006年1月的一个开源项目,强调理念是“write less,do more”,压缩后大小30KB左右.. 2,jQuery里的方法都被设计程自动操作对象集合,而 ...
- JQuery选择器——《锋利的JQuery》
刚学CSS的时候我们已经接触了选择器,其实就是按照一定的规则选择出来我们想要获取到的元素.在这里,既然选择了用jQuery选择器,首先来谈谈JQuery选择器的优势: 1.简洁的写法:$()函数在很多 ...
- 2 《锋利的jQuery》jQuery选择器
tip1:jquery检查某个元素是否存在:if($("#tt").length>0){}或者if($("#tt")[0]){} 先说css选择器有: 标 ...
- 锋利的jQuery ——jQuery选择器(二)
一.jQuery选择器 1)CSS选择器 CSS选择器有:1>标签选择器 E{CSS规则} 2>ID选择器 #ID{CSS规则} 3>类选择器 E.className{CSS ...
- 锋利的jQuery学习笔记之jQuery选择器
在介绍jQuery选择器之前,先简单介绍一下CSS选择器---> 一.CSS选择器 常见的CSS选择器有以下几种: 选择器 语法 描述 示例 标签选择器 E{CSS规则} 以文档元素为选择符 t ...
随机推荐
- Tiled Map地图编辑器键盘快捷键
Tiled是款不错的地图编辑器,不过快捷键真是隐蔽啊,不看github上得wiki根本不知道,用的过程中查英文文档总是觉得慢,所以翻译成了中文. 通用 右键点击图块(tile):复制图块到图章刷(拖动 ...
- 用Java导出为excel表格
导出的是最基础的excel表格,没有任何样式. <input type="button" value="输出到Excel" onclick='output ...
- px4flow通过iic读取具体寄存器数据程序
底层通信用了昨天写好的iic,今天结合官方资料成功读出所有指定寄存器的数据附上源码 include.h主要包括了一些stm32 IO控制的宏定义,具体参考正点原子所有例程中都有的sys.h头文件 in ...
- Swift基础语法(三)
Array数组在swift中Array相当于oc中的NSMutableArray(变长数组) //1.定义数组 var numarr:Int[] = [,,,,]; var strarr:String ...
- 两个list<object> 比较 得到相同数据 差异数据
package com.lizi.admin.utils.contrast;import java.lang.reflect.InvocationTargetException;import java ...
- JQuery按回车提交数据
引入JQuery文件 <script src="JS/jquery-1.9.1.js" type="text/javascript"></sc ...
- <Oracle Database>后台进程
进程监视器进程(PMON) 这个进程负责在出现异常中止的连接之后完成清理.PMON会回滚未提交的工作,并释放为失败进程分配的SGA资源.PMON还负责监视其他的Oracle后台进程,并在必要时(如果 ...
- Hyper-V初涉:功能的添加与虚拟机的创建
Hyper-V是微软提供的一款高效率的虚拟化管理软件,在早期的Windows服务器中配备Hyper-V组件,Windows 8是首次将企业用Hyper-V集成在个人系统中,可见虚拟化技术的发展之迅速. ...
- hdu 5720
考虑三个树枝:a,b,c若c是将要抛出的树枝,那么形成三角形的条件是a+b>c and a-b<c 可以写成 c属于开区间(a-b,a+b)对于每个C和许许多多的其他边,如何保证C不构成三 ...
- jsti 和EL用法注意点
今天使用stl 结合El做jsp页面展现,出现了个问题,怎么调也调不好,最后将jstl的源码拿来跟踪调了一下才明白其中的道理. 在使用jstl tag <c:forEach var=" ...
