如何将Virtualbox和VMware虚拟机相互转换[译文211] - 转

迁移到其他的虚拟机程序可行会吓倒一批人。如果你已经按照自己的喜好设置好了虚拟机，那么就不需要再从头安装——你可以迁移现有的虚拟机。

VirtualBox 和 VMware 使用不同的虚拟机格式，不过他们都支持标准的开放式虚拟化格式。将已经存在的虚拟机转换为 OVF/OVA 格式就可以导入其他的虚拟机程序。

不幸的是，这并不总是奏效。因为 VirtualBox 和 VMware 看起来使用些许不同的 OVA/OVF 实现方式，因此也不完全兼容。如果这不奏效，你可能需要重新安装虚拟机的客户机操作系统了。

VirtualBox 转换到 VMware

在迁移 Virtualbox（以下简称 Vbox —— 译者注） 虚拟机到 VMware 之前，确保在 Vbox 中虚拟机“已关闭”——而不是挂起。如果是挂起状态，启动虚拟机然后关掉它。

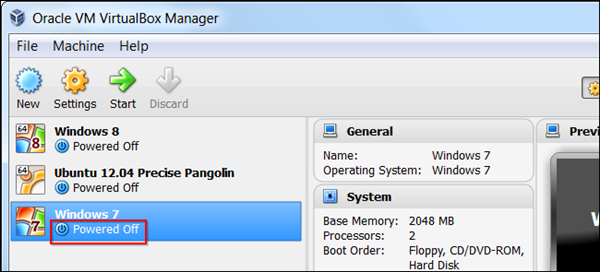
点击 Vbox 管理菜单，选择导出虚拟电脑。

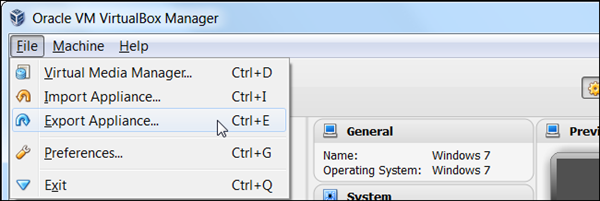
选择要导出的虚拟机并选择文件保存位置。

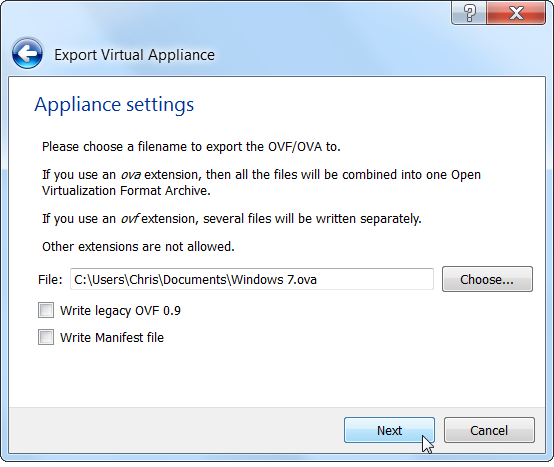
Vbox 会创建一个开放式虚拟化格式包（OVA 文件）使得 VMware 可以导入。根据虚拟机磁盘文件的大小，此过程需稍等一段时间。

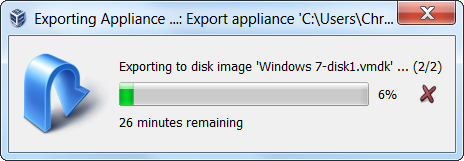
要将此 OVA 文件导入 VMware，点击打开虚拟机选项并找到你的 OVA 文件。

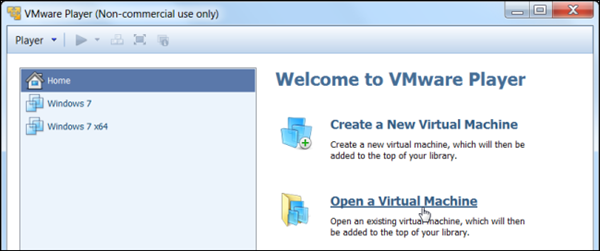
VirtualBox 和 VMware 不是完美兼容，所以你可能会看到一个警告信息，告诉你文件“不能通过OVF规格一致性验证”——不过如果你点击重试，可能会导入并成功运行虚拟机。

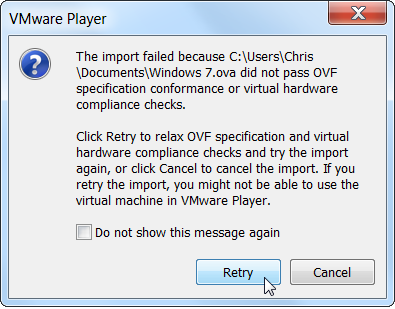
过程结束之后，你可以在在 VMware 中启动虚拟机，在虚拟机控制面板中卸载 Vbox 增强功能（VirtualBox Guest Additions），在虚拟机菜单中安装 VMware 工具。

VMware 转换到 VirtualBox

在将 VMware 虚拟机迁移到 Vbox 之前，确保在 VMware 的状态为“关闭电源” —— 非挂起。如果是挂起，启动虚拟机然后关机。

接下来，找到 OVFTool 所在目录。如果你用的是 VMware Player，目录在类似 C:\Program Files (x86)\VMware\VMware Player\OVFTool。按住 Shift 键，右击选择在此处打开命令行窗口。

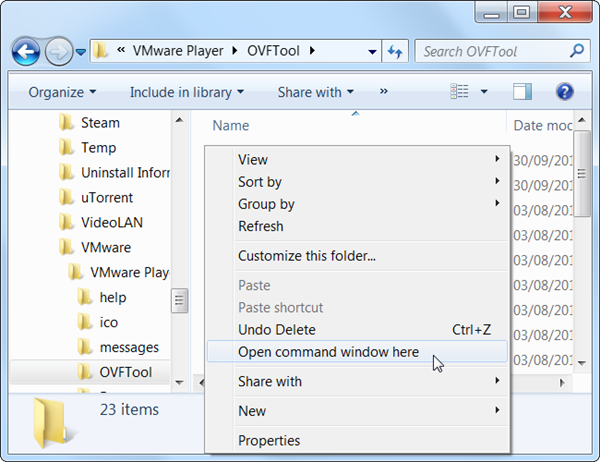
按照下列语法运行 ovftool：

ovftool source.vmx export.ovf

例如，如果我们转换位于 C:\Users\NAME\Documents\Virtual Machines\Windows 7 x64\Windows 7 x64.vmx 的虚拟机，并且创建 OVF 位于 C:\Users\NAME\export.ovf，我们需要执行下列命令：

ovftool “C:\Users\NAME\Documents\Virtual Machines\Windows  x64\Windows  x64.vmx” C:\Users\NAME\export.ovf

如果提示“打开此盘失败”错误，很可能是虚拟机仍在运行或者没有正确关机——启动虚拟机并执行关机操作。

过程结束之后，可以使用管理菜单中的导入虚拟电脑选项，将 .ovf 文件导入 Vbox。

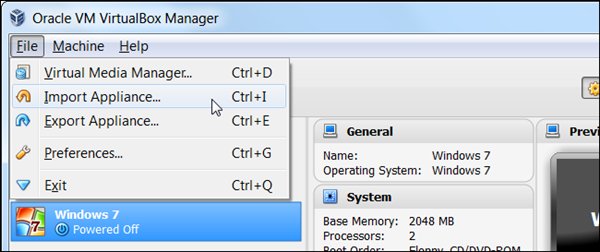
导入完成之后，你可以启动虚拟机，卸载 VMware 工具，并安装 Virtualbox 客户机增强工具。