递归实现快速幂（C++版）

快速幂是什么？

顾名思义，快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高。

就以a的b次方来介绍：

把b转换成二进制数，该二进制数第i位的权为

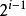
例如：

11的二进制是1011

11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1

因此，我们将a¹¹转化为算

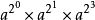
如何编写快速幂代码？

以下是用C++语言编写的两种代码，可供各位参考：

 //快速幂1（数字较小）：
 #include<bits/stdc++.h>
 using namespace std;
 long long f(long long n,long long m)
 {
     //求的是m个n相乘，这里n是一个正整数
     if(m==)return ;
     else if(m==)return n;
     else if(m%==)return f(n*n,m/);//偶数时的降幂
     return f(n*n,m/)*n;//奇数时的降幂
 }
 int main()
 {
     long long n,m;
     cin>>n>>m;
     cout<<f(n,m);
     return ;
 }

 //快速幂2（数字较大）：
 #include<bits/stdc++.h>
 using namespace std;
 int k;
 long long f(long long n,long long m)
 {
     //求的是m个n相乘，这里n是一个正整数
     if(m==)return ;
     else if(m==)return n%k;
     else if(m%==)return f((n%k)*(n%k),m/)%k;//偶数时的降幂
     return f((n%k)*(n%k),m/)*(n%k)%k;//奇数时的降幂
 }
 int main()
 {
     long long n,m;
     cin>>n>>m>>k;
     cout<<f(n,m);
     return ;
 }

记住一点：数字较大的时候只要把原先的程序能模（%）的都模掉，否则数据太大，容易报表！

下面给大家一道题提升一下，如果大家有想法，可以私信我哦！（下期告诉大家参考答案）

题目描述 Description
有n头奶牛住在n个环形的牛圈，奶牛编号为0到n-1，牛圈编号也为0到n-1，i号牛住在第i号牛圈。
现在牛们想实施住宅滚动制度。每滚动一次，第0号圈的奶牛会顺时针搬到第m号牛圈中，第1号圈的奶牛会顺时针搬到第1+m号牛圈中，...，第n-m号圈的奶牛会顺时针搬到0号牛圈，
也就是说原来的第i号牛圈的奶牛会顺时针搬到i+m号牛圈。
试判断，进行了10^k轮滚动后，原来在x号圈的奶牛现在在几号牛圈。

输入描述 Input Description
一行，四个正整数，n m k x

输出描述 Output Description
10^k轮后，最初在第x个圈的奶牛所处牛圈的编号

样例输入 Sample Input
10 3 4 5

样例输出 Sample Output
5

数据范围及提示 Data Size & Hint
对于 30%的数据，0 < k < 7；
对于 80%的数据，0 < k < 10^7；
对于 100%的数据，1 < n < 1,000,000，0 < m < n，1 <= x <=n，0 < k < 10^9。