URAL1519 Formula 1 【插头dp】

题目链接

URAL1519

题解

看题型显然插头\(dp\)

考虑如何设计状态



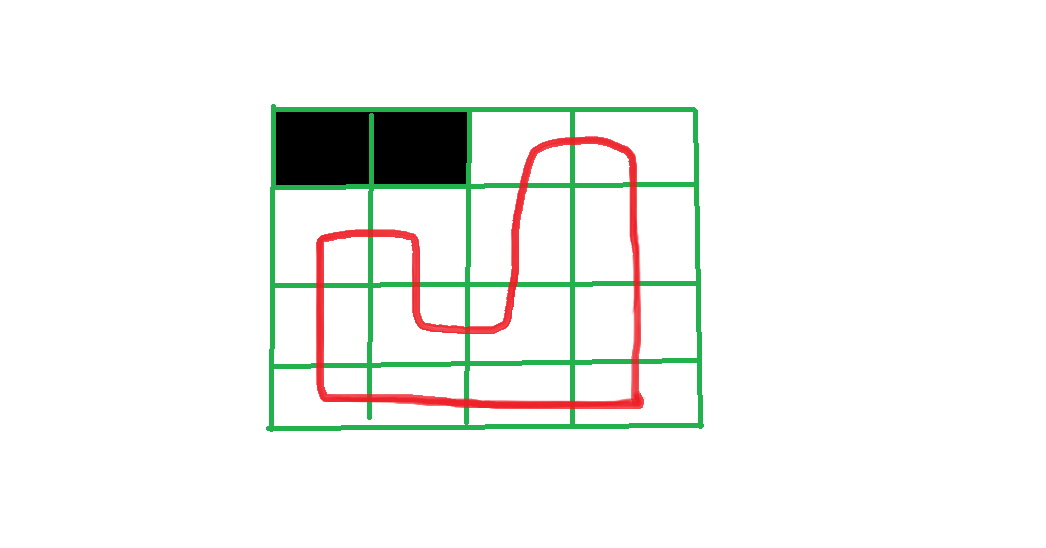
有这样一个方案

当我们决策到某个位置

轮廓线长这样



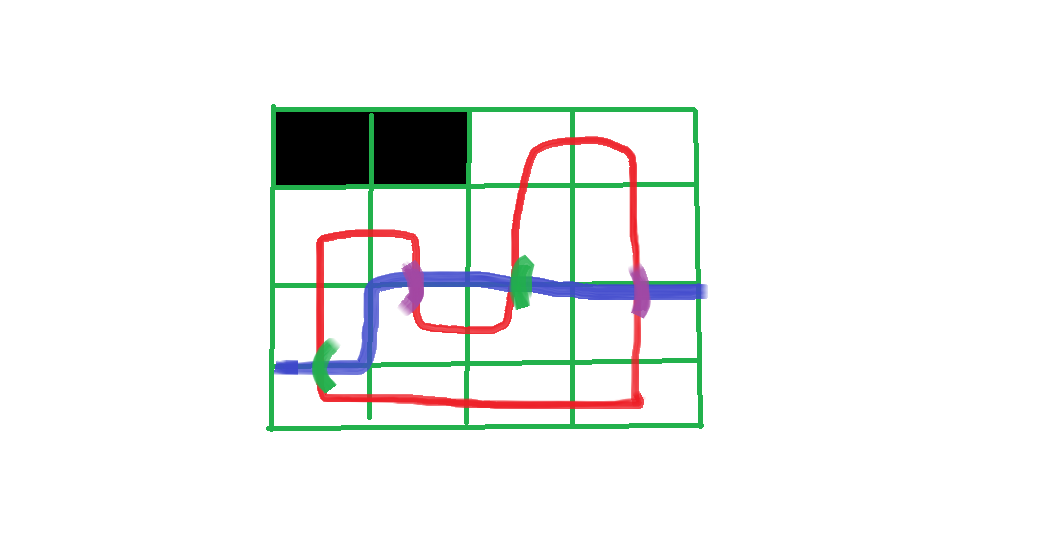
你会发现插头一定是相互匹配的

所以我们实际上可以把状态用括号序列表示

如上图就是(#)()

是一个三进制数

那么我们设\(f[i][j][s]\)表示决策到\((i,j)\)，轮廓线状态为\(s\)的方案数

我们同时记\(0\)为空插头，\(1\)为表示左括号的插头，\(2\)为表示有括号的插头

先不管空间问题，我们考虑一下转移

有比较多的情况

我们记\(b1\)，\(b2\)为\((i,j)\)的左、上插头

\(b1 = 0,b2 = 0\)

首先如果\((i,j)\)本身是障碍格，那么它右插头和下插头也为\(0\)

否则如果对应方向没有障碍，\((i,j)\)右下插头为\(12\)

\(b1\)和\(b2\)有一者为\(0\)，那么转移的时候另一个括号的位置放哪里都可以，只需要判断有无障碍

\(b1\)和\(b2\)为同一种括号，我们只需往另一侧查找匹配的括号，改变方向

例如((#))变为###()

如图所示：



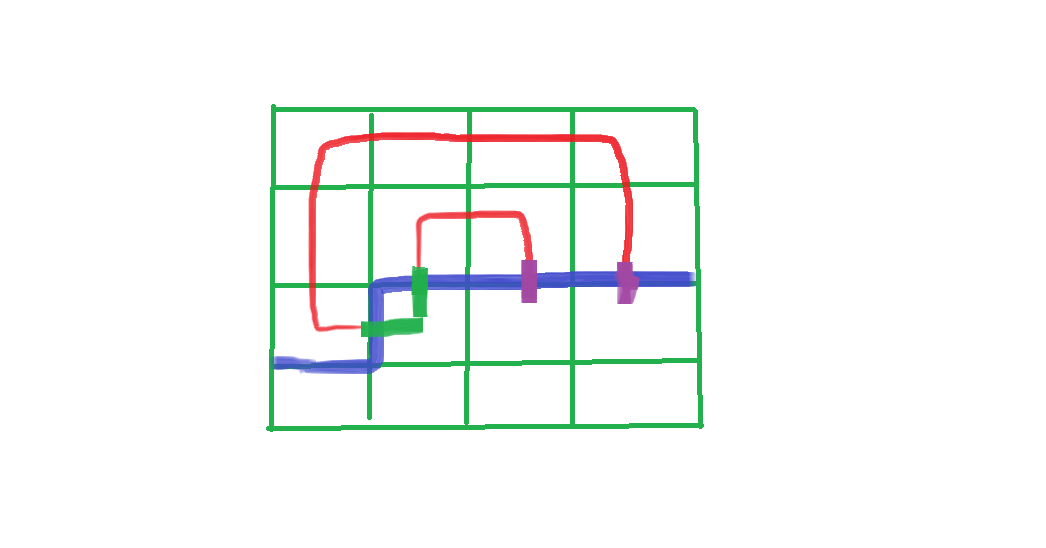
把左边两个连起来，右边两个插头就变成了匹配的括号

即由((#))变为###()

\(b1 = 2\)且\(b2 = 1\)

就是(#)(#)这种情况，可以变为(####)

\(b1 = 1\)且\(b2 = 2\)

除非是最后一个格子，否则不能贸然连起来，不然就会出现不连通的情况

具体实现的时候，可以使用四进制而结合位运算加快速度

由于空间比较小，我们需要滚动数组，并且使用\(hash\)表储存状态

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#include<vector>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 13,maxm = 5000000,INF = 1000000000,P = 201611;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
	return out * flag;
}
int n,m,sx,sy;
char S[maxn][maxn];
int now,tot[2],h[2][P],nxt[2][maxm],num[2][maxm];
LL f[2][maxm],ans;
inline void add(int s,LL x){
	int tmp = s % P;
	for (int k = h[now][tmp]; k; k = nxt[now][k])
		if (num[now][k] == s){f[now][k] += x; return;}
	nxt[now][++tot[now]] = h[now][tmp]; h[now][tmp] = tot[now];
	num[now][tot[now]] = s; f[now][tot[now]] = x;
}
inline bool isok(int x,int y){
	return x >= 1 && x <= n && y >= 1 && y <= m && S[x][y] != '*';
}
void work(){
	int las = 1,e,s,b1,b2;
	LL x;
	f[0][1] = tot[0] = 1; num[0][1] = 0;
	for (int i = 1; i <= n; i++){
		for (int k = 1; k <= tot[now]; k++) num[now][k] <<= 2;
		for (int j = 1; j <= m; j++){
			now ^= 1; las ^= 1;
			cls(h[now]); tot[now] = 0;
			for (int k = 1; k <= tot[las]; k++){
				s = num[las][k]; x = f[las][k];
				b1 = (s >> (j - 1 << 1)) & 3;
				b2 = (s >> (j << 1)) & 3;
				e = s ^ (b1 << (j - 1 << 1)) ^ (b2 << (j << 1));
				if (b1 == 0 && b2 == 0){
					if (S[i][j] == '*') add(e,x);
					else if (isok(i + 1,j) && isok(i,j + 1))
						add(e | (1 << (j - 1 << 1)) | (2 << (j << 1)),x);
				}
				else if (b1 == 0){
					if (isok(i,j + 1)) add(s,x);
					if (isok(i + 1,j)) add(e | (b2 << (j - 1 << 1)),x);
				}
				else if (b2 == 0){
					if (isok(i + 1,j)) add(s,x);
					if (isok(i,j + 1)) add(e | (b1 << (j << 1)),x);
				}
				else if (b1 == 1 && b2 == 1){
					int cnt = 1;
					for (int p = j + 1; p <= m + 1; p++){
						if ((e >> (p << 1) & 3) == 1) cnt++;
						if ((e >> (p << 1) & 3) == 2) cnt--;
						if (!cnt){add(e ^ (3 << (p << 1)),x); break;}
					}
				}
				else if (b1 == 2 && b2 == 2){
					int cnt = 1;
					for (int p = j - 2; ~p; p--){
						if ((e >> (p << 1) & 3) == 2) cnt++;
						if ((e >> (p << 1) & 3) == 1) cnt--;
						if (!cnt){add(e ^ (3 << (p << 1)),x); break;}
					}
				}
				else if (b1 == 2 && b2 == 1) add(e,x);
				else if (i == sx && j == sy) ans += x;
			}
		}
	}
	printf("%lld\n",ans);
}
int main(){
	n = read(); m = read();
	REP(i,n) scanf("%s",S[i] + 1);
	REP(i,n) REP(j,m) if (S[i][j] == '.') sx = i,sy = j;
	work();
	return 0;
}