Nuske vs Phantom Thnook

Nuske vs Phantom Thnook

---

Time limit : 4sec / Memory limit : 256MB

Score : 700 points

Problem Statement

Nuske has a grid with N rows and M columns of squares. The rows are numbered 1 through N from top to bottom, and the columns are numbered 1 through M from left to right. Each square in the grid is painted in either blue or white. If Si,j is 1, the square at the i-th row and j-th column is blue; if Si,j is 0, the square is white. For every pair of two blue square a and b, there is at most one path that starts from a, repeatedly proceeds to an adjacent (side by side) blue square and finally reachesb, without traversing the same square more than once.

Phantom Thnook, Nuske's eternal rival, gives Q queries to Nuske. The i-th query consists of four integers xi,1, yi,1, xi,2 and yi,2 and asks him the following: when the rectangular region of the grid bounded by (and including) the xi,1-th row, xi,2-th row, yi,1-th column and yi,2-th column is cut out, how many connected components consisting of blue squares there are in the region?

Process all the queries.

Constraints

• 1≤N,M≤2000
• 1≤Q≤200000
• Si,j is either 0 or 1.
• Si,j satisfies the condition explained in the statement.
• 1≤xi,1≤xi,2≤N(1≤i≤Q)
• 1≤yi,1≤yi,2≤M(1≤i≤Q)

---

Input

The input is given from Standard Input in the following format:

N M Q
S1,1..S1,M
:
SN,1..SN,M
x1,1 yi,1 xi,2 yi,2
:
xQ,1 yQ,1 xQ,2 yQ,2

Output

For each query, print the number of the connected components consisting of blue squares in the region.

---

Sample Input 1

Copy

3 4 4
1101
0110
1101
1 1 3 4
1 1 3 1
2 2 3 4
1 2 2 4

Sample Output 1

Copy

3
2
2
2

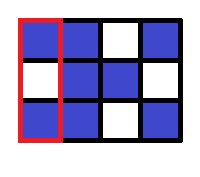
In the first query, the whole grid is specified. There are three components consisting of blue squares, and thus 3 should be printed.

In the second query, the region within the red frame is specified. There are two components consisting of blue squares, and thus 2 should be printed. Note that squares that belong to the same component in the original grid may belong to different components.

---

Sample Input 2

Copy

5 5 6
11010
01110
10101
11101
01010
1 1 5 5
1 2 4 5
2 3 3 4
3 3 3 3
3 1 3 5
1 1 3 4

Sample Output 2

Copy

3
2
1
1
3
2

题意: n*m (n,m<=2000) 的地图，q (q<=200000)次询问，地图每个格子非蓝即白，上下相连，或者左右相连算作连续，还有，每两个蓝色格子，如果连通，保证只有一条确定路径相连，对于每次询问，求范围矩形蓝色连通块个数。

//题解：这题，题意都读了很久。。。常规求连通的算法会超时，因为Q很大。对于每两个连通蓝色格子，只有一条路径连通很关键，每个连通块就变成了一颗树，，所以，即求森林个数，树的话有个性质，点数减边数等于1，所以，即求范围内点数减边数，查询时间复杂度为 O(1)

思路明白，代码比较好写

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 using namespace std;
 #define LL long long
 #define INF 0x3f3f3f3f
 #define MX 2005

 int n,m,q;
 int ans;
 char mp[MX][MX];
 int d[MX][MX];  //点
 int x[MX][MX];  //线
 int up[MX][MX]; //上相连
 int lef[MX][MX];//左相连

 void slv()
 {
     memset(x,,sizeof(x));
     memset(d,,sizeof(d));
     memset(up,,sizeof(up));
     memset(lef,,sizeof(lef));
     for (int i=;i<=n;i++)
     {
         for (int j=;j<=m;j++)
         {
             d[i][j]=d[i-][j]+d[i][j-]-d[i-][j-];
             x[i][j]=x[i-][j]+x[i][j-]-x[i-][j-];
             up[i][j]=up[i][j-];
             lef[i][j]=lef[i-][j];
             if (mp[i][j]=='')
             {
                 d[i][j]++;
                 if (i>&&mp[i-][j]=='') x[i][j]++;
                 if (j>&&mp[i][j-]=='') x[i][j]++;
                 if (i>&&mp[i-][j]=='') up[i][j]++;
                 if (j>&&mp[i][j-]=='') lef[i][j]++;
             }
         }
     }
 }

 int main()
 {
     scanf("%d%d%d",&n,&m,&q);

     for (int i=;i<=n;i++)
         scanf("%s",mp[i]+);

     slv();

     while (q--)
     {
         int x1,y1,x2,y2;
         scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
         if (x1>x2) swap(x1,x2);
         if (y1>y2) swap(y1,y2);
         int ans = d[x2][y2]-d[x2][y1-]-d[x1-][y2]+d[x1-][y1-];

         ans -= x[x2][y2]-x[x2][y1-]-x[x1-][y2]+x[x1-][y1-];
         ans += up[x1][y2]-up[x1][y1-];
         ans += lef[x2][y1]-lef[x1-][y1];

         cout<<ans<<endl;
     }
     return ;
 }