【BZOJ3944/4805】Sum/欧拉函数求和 杜教筛

【BZOJ3944】Sum

Description

Input

一共T+1行

第1行为数据组数T(T<=10)

第2~T+1行每行一个非负整数N，代表一组询问

Output

一共T行，每行两个用空格分隔的数ans1,ans2

Sample Input

6
1
2
8
13
30
2333

Sample Output

1 1
2 0
22 -2
58 -3
278 -3
1655470 2

题解：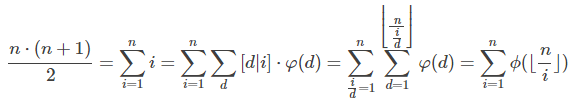

当i等于1时就是答案，剩余的部分递归算下去就行了（先预处理出1000000以内的答案，其余的答案要用map保存）

粘自http://blog.csdn.net/skywalkert/article/details/50500009

求莫比乌斯函数的前缀和类似，从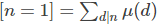开始推就好了

#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <utility>
#define MP(A,B) make_pair(A,B)
using namespace std;
const int m=3000000;
typedef long long ll;
int n,num;
ll phi[m+10],mu[m+10],sp[m+10],sm[m+10],pri[m+10];
bool np[m+10];
typedef pair<ll,ll> pll;
map<ll,pll>	mp;
pll dfs(ll x)
{
	if(x<=m)	return MP(sp[x],sm[x]);
	if(mp.find(x)!=mp.end())	return MP(mp[x].first,mp[x].second);
	ll rp=x*(x+1)>>1,rm=1,i,last;
	for(i=2;i<=x;i=last+1)
	{
		last=x/(x/i);
		pll tmp=dfs(x/i);
		rp-=tmp.first*(last-i+1);
		rm-=tmp.second*(last-i+1);
	}
	mp[x]=MP(rp,rm);
	return MP(rp,rm);
}
int main()
{
	int T,i,j;
	scanf("%d",&T);
	phi[1]=sp[1]=mu[1]=sm[1]=1;
	for(i=2;i<=m;i++)
	{
		if(!np[i])	pri[++num]=i,phi[i]=i-1,mu[i]=-1;
		sp[i]=sp[i-1]+phi[i],sm[i]=sm[i-1]+mu[i];
		for(j=1;j<=num&&i*pri[j]<=m;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				phi[i*pri[j]]=phi[i]*pri[j];
				mu[i*pri[j]]=0;
				break;
			}
			mu[i*pri[j]]=-mu[i];
			phi[i*pri[j]]=phi[i]*(pri[j]-1);
		}
	}
	while(T--)
	{
		ll a;
		scanf("%lld",&a);
		pll tmp=dfs(a);
		printf("%lld %lld\n",tmp.first,tmp.second);
	}
	return 0;
}