动态规划：LCS

先上状态转移方程，还是很容易看明白的

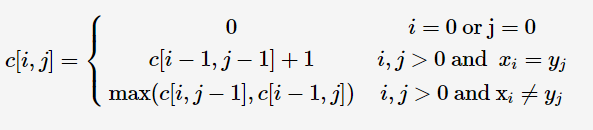
例题是Codevs的1862，这个题不是实现了方程就可以了的，还要完成一个事情那就是计数，数一数到底有多少个最长公共子序列

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int maxn=;
 const int p=1e8;
 char a[maxn],b[maxn];
 int dp[maxn][maxn],f[maxn][maxn];
 int main()
 {
     scanf("%s%s",a+,b+);
     int al=strlen(a+)-;
     int bl=strlen(b+)-;
     for(int i=;i<=al;i++) f[i][]=;
     for(int i=;i<=bl;i++) f[][i]=;
     for(int i=;i<=al;i++)
         for(int j=;j<=bl;j++)
         {
             if(a[i]==b[j])
             {
                 dp[i][j]=dp[i-][j-]+;
                 int k1=,k2=;
                 if(dp[i][j]==dp[i-][j]) k1=;
                 if(dp[i][j]==dp[i][j-]) k2=;
                 f[i][j]=f[i-][j-]+(k1*f[i-][j])+(k2*f[i][j-]);
                 f[i][j]=(f[i][j]+p)%p;
             }
             else
             {
                 dp[i][j]=max(dp[i-][j],dp[i][j-]);
                 int k1=,k2=,k3=;
                 if(dp[i][j]==dp[i-][j]) k1=;
                 if(dp[i][j]==dp[i][j-]) k2=;
                 if(dp[i][j]==dp[i-][j-]) k3=;
                 f[i][j]=(k1*f[i-][j])+(k2*f[i][j-])-(k3*f[i-][j-]);
                 f[i][j]=(f[i][j]+p)%p;
             }
         }
     printf("%d\n%d\n",dp[al][bl],f[al][bl]);
     return ;
 }

在这里我们用dp记录长度，用f记录个数

由于输入是以“.”结尾的，所以读入的时候有些许的变化

    scanf("%s%s",a+,b+);
    int al=strlen(a+)-;
    int bl=strlen(b+)-;

这样读入的时候真正的字符串的下标是从a+1开始的，循环的时候从1开始循环，到strlen(a+1)结束

因为结尾字符不属于串，所以给al--就好了