Encrypted bootloader (程序BIN文件加密及在线升级）

了解更多关于bootloader 的C语言实现，请加我QQ: 1273623966 （验证信息请填 bootloader）,欢迎咨询或定制bootloader（在线升级程序）。

在上一个博客随笔，我介绍了为PIC16，PIC18, PIC24/dsPIC, PIC32的学习板或最小系统板做的Xmodem bootloader。今天给大家介绍在我的Xmodem bootloader 的基础上开发的Encrypted bootloader。今年的国庆节，我哪都没去，就宅在家里把Encrypted bootloader完成。虽然我叫它Encrypted bootloader, 实际上加密(encrypted)的是应用程序BIN文件，加密过的BIN文件传送给单片机，单片机的boot程序先(decrypting)解密然后烧写数据到单片机ROM的对应的地址上。所以整个Encrypted bootloader工程分为两部分，一部分是PC端的工程，完成将Hex文件转换为BIN文件, 然后将BIN文件加密生成.ecd文件(采用XTEA的加密方式)，最后作为Xmodem的发送端将.ecd文件按照XMODEM协议发送到单片机；另一部分是单片机端的工程(Encrypted boot)，做为Xmodem接收端接收从PC端发送过来加密过的数据，解密并完成烧写。

　　XTEA

　　XTEA (Extended Tiny Encryption Algorihtm)是TEA的一个变种版本。XTEA采用对称加密，将明文分成多个等长的组，并用相同的密码算法和密钥对每组分别进行加密和解密。密钥长度为128位，加密块为64位。XTEA算法是David Wheeler and Roger Needham于1997年发布的，并附带有C语言的实现源代码。

#include <stdint.h>

/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */

void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
    for (i=0; i < num_rounds; i++) {
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
        sum += delta;
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
    }
    v[0]=v0; v[1]=v1;
}

void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
    for (i=0; i < num_rounds; i++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
        sum -= delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
    }
    v[0]=v0; v[1]=v1;
}

　　在我的Encrypted bootloader工程里面，XTEA是用C#通过扩展.NET SymmetricAlgorithm Class实现的，有用户交互界面，并支持一键式随机生成加密密钥（不过要记住哦，因为解密需要同样的密钥）。下面贴上图片介绍下加密过程。

　　加密过程

　　1. 用MPLAB X v3.30生成的PIC hex文件。

　　2. 用C#写的工具将Hex转换为Bin,

　　

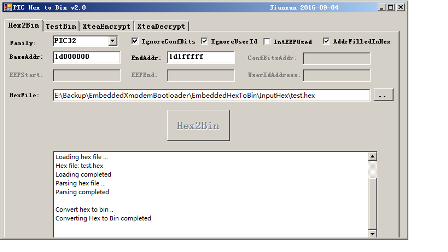
　　转换成BIN后再打开是如下。

　　没错，Bin直接打开，是乱码的，就像我们打开.exe文件那样。Bin文件虽然不可视，但是如果直接把Bin文件发给代工厂家，或协作商，还是不安全的。它是可以通过其他工具解读出里面的内容的，并可以直接使用。所以需要加密。下面是用C#写的加密工具界面。

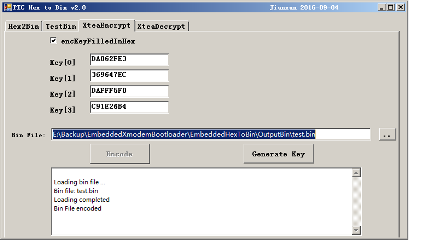
　　这样，应用程序的BIN文件加密后，就很安全了，你可以发给供应商也可以发给客户了，没有密钥，是很难解密出里面的内容的，没有解密，是不能直接使用的。

Bin文件加密后，通过XMODEM SEND发送给单片机，单片机需要预装带XTEA decrypting（解密）功能的Xmodem bootloader.

Encrypted Boot

     Encrypted Boot是运行在单片机的小程序，首先它是XMODEM的接收端，接收加密过的数据，然后如同上面所贴代码中decipher()那样解密数据，所用密钥必须是加密时所用的密钥。最后将解密后的数据烧写到单片机的ROM指定的位置中去。这样就实现了可靠又安全地应用程序在线升级。如果有兴趣进一步了解和讨论我的Encrypted bootloader, 欢迎发送短消息或email给我，我的Q扣：1273623966。