HDU1054 Strategic Game（最小点覆盖）

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 10153    Accepted Submission(s): 4744

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1054

Description:

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:

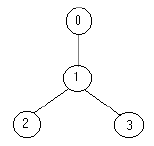
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

Sample Input:

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

Sample Output:

1
2

题意：

问在图中最少放置多少个士兵，可以看守所有的边。

题解：

最小点覆盖模板。

但由于数据量较大，边数较多，邻接矩阵要超时，我便改用vector存储。

代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <vector>
#define mem(x,y) memset(x,y,sizeof(x))
using namespace std;

const int N =  ;
int check[N],match[N];
int n,ans,dfn;
vector<int> link[N];

inline int dfs(int x){
    for(int i=;i<link[x].size();i++){
        int now = link[x][i];
        if(check[now]!=dfn){
            check[now]=dfn;
            if(match[now]==- || dfs(match[now])){
                match[now]=x;
                return ;
            }
        }
    }
    return ;
}

int main(){
    while(scanf("%d",&n)!=EOF){
        for(int i=;i<n;i++) link[i].clear();
        mem(link,);mem(match,-);ans=dfn=;
        for(int i=,u,k;i<n;i++){
            scanf("%d:(%d)",&u,&k);
            for(int j=,v;j<=k;j++){
                scanf("%d",&v);
                link[u].push_back(v);
                link[v].push_back(u);
            }
        }
        for(int i=;i<n;i++){
            dfn++;
            if(dfs(i)) ans++;
        }
        printf("%d\n",ans/);
    }
    return ;
}