数据结构之最小堆的实现C++版

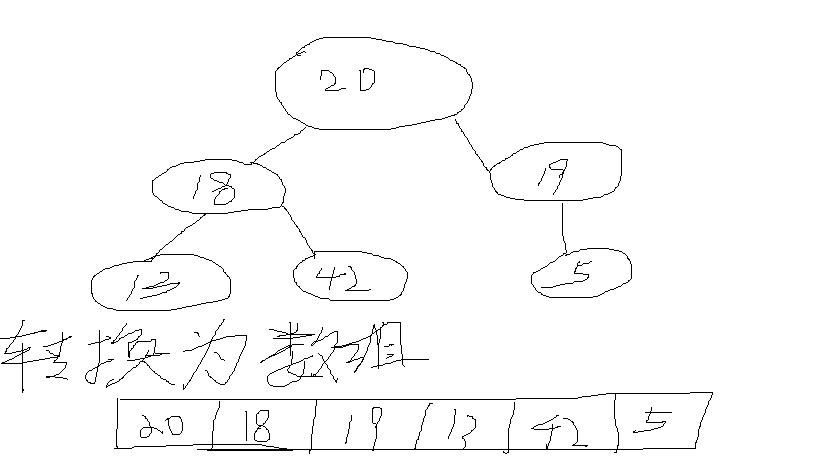
完全二叉树之所以用数组的方式存在，在于他的一个特性 若子节点为i,则父节点为（i-1）/2，注意c++特性，该结果肯定是个整数。

若父节点为j,则子节点必为2*j+1;则在数组里面可以非常方便的通过下标去获取。

建堆的核心思想:

　　堆在index的值为heap[index]，然后其两个孩子的值边可求得，左孩子为heap[index*2+1]，右孩子为heap[index*2+2]。

首先比较左边孩子与右边孩子，获取较小值的孩子，然后让heap[index]与值较小的孩子进行比较。若值小则交换值，并且移动index到值较小孩子的位置，否则退出调整。

下面看代码，有注释：

#pragma once
template<class T>
class JBMinHeap
{
private:
    //申请堆空间
    T *_minHeap = NULL;
    int _index,_maxSize;
public:
    JBMinHeap(int maxSize) {
        _maxSize = maxSize;
        _minHeap = new T[_maxSize];
        _index = -;
    }
    JBMinHeap(JBMinHeap &h) {
        _index = h._index;
        _maxSize = h._maxSize;
        _minHeap = new T[_maxSize];
        for (int i = ;i<_maxSize) {
            *_minHeap[i] = *h._minHeap[i];
        }
    }
    ~JBMinHeap() {
        delete[]_minHeap;
    }
    //获取整个最小堆的头部指针
    T * getMinHeap() {
        return _minHeap;
    }
    //判断堆是不是空的
    bool isEmpty() {
        return _index == -;
    }
    bool add(T x) {
        if (isFull()) {
            return false;
        }
        _index++;
        _minHeap[_index] = x;
        return true;
    }
    bool isFull() {
        return _index == _maxSize;
    }
    //堆进行向下调整
    void adjustDown(int index);
    //队进行向上调整
    void adjustUp(int index);
    //建堆运算
    void createMinHeap() {
        if (isEmpty()) {
            return;
        }
        for (int i = (_index-)/;i >-;i--) {//直接从倒数第二层 逐层向下调整
            adjustDown(i);
        }
    }
};
template<class T>
void JBMinHeap<T>::adjustDown(int index) {
    if (isEmpty()) {
        return;
    }
    while (index<_index)
    {
        T temp = _minHeap[index];//将当前索引的位置的值保存下来
        int oneC =  * index + ;//获取到两个孩子的位置
        int twoC =  * index + ;
        if (oneC == _index) {//若第一个孩子是整个堆最后一个位置 则直接执行交换操作并结束执行
                _minHeap[index] = _minHeap[oneC];
                _minHeap[oneC] = temp;
                return;
        }
        if (twoC >_index) {//如果第二个孩子的索引位置越界 结束执行
            return;
        }
        if (_minHeap[oneC] <= _minHeap[twoC]) {//正常情况的数据交互执行
            if (temp > _minHeap[oneC]) {
                _minHeap[index] = _minHeap[oneC];
                _minHeap[oneC] = temp;
                index = oneC;
            }
            else {//如果该处索引值已经是比两个孩子小 则结束循环
                index = _index;
            }
        }
        else
        {
            if (temp > _minHeap[twoC]) {
                _minHeap[index] = _minHeap[twoC];
                _minHeap[twoC] = temp;
                index = twoC;
            }
            else
            {
                index = _index;
            }
        }
    }
}
template<class T>
void JBMinHeap<T>::adjustUp(int index) {
    if (index > _index) {//大于堆的最大值直接return
        return;
    }
    while (index>-)
    {
        T temp = _minHeap[index];
        int father = (index - ) / ;
        if (father >= ) {//若果索引没有出界就执行想要的操作
            if (temp < _minHeap[father]) {
                _minHeap[index] = _minHeap[father];
                _minHeap[father] = temp;
                index=father;
            }
            else {//若果已经是比父亲大 则直接结束循环
                index = -;
            }
        }
        else//出界就结束循环
        {
            index = -;
        }
    }
}

主程序：

#include "stdafx.h"
#include"stdlib.h"
#include"JBQueue.h"
#include"JBStack.h"
#include"JBBinaryTree.h"
#include"JBMinHeap.h"

int main()
{
    {
        JBMinHeap<int> jb();
        jb.add();
        jb.add();
        jb.add();
        jb.add();
        jb.add();
        jb.add();
        jb.createMinHeap();
        int *p=jb.getMinHeap();
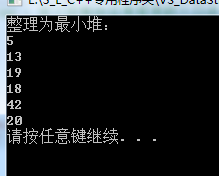
        printf("整理为最小堆：\n");
        for (int i = ;i < ;i++) {
            printf("%d\n",p[i]);
        }
    }
    system("pause");
    return ;
}