codeforces 789 C. Functions again（dp求区间和最大）

题目链接：http://codeforces.com/contest/789/problem/C

题意：就是给出一个公式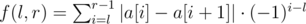

然后给出一串数求一个区间使得f(l,r)最大。

这题需要一个小小的处理

可以设数组b[i]和c[i]

if i % 2 == 0

b[i]=abs(a[i]-a[i+1])

c[i]=-abs(a[i]-a[i+1])

else

b[i]=-abs(a[i]-a[i+1])

c[i]=abs(a[i]-a[i+1])

然后就是求两个数组的区间和的最大值这个方法就不介绍了

至于为什么要分b，c两个数组，很简单，因为f都是一正一负的所以取的首位是什么那么接下来的正负就定了

但是这个数列不论怎么去就只有两种取法就是这两种。

#include <iostream>
#include <cstring>
#define inf 0X3f3f3f3f
using namespace std;
typedef long long ll;
const int M = 1e5 + 10;
int a[M] , b[M] , c[M];
ll dp[M][3][3];
int Abs(int x) {
    if(x < 0)
        return -x;
    return x;
}
int main() {
    int n;
    scanf("%d" , &n);
    for(int i = 1 ; i <= n ; i++) {
        scanf("%d" , &a[i]);
    }
    ll MAX1 = 0 , MAX2 = 0 , sum1 = 0 , sum2 = 0;
    for(int i = 1 ; i < n ; i++) {
        if(i % 2 == 0) {
            b[i] = Abs(a[i] - a[i + 1]);
            c[i] = -1 * Abs(a[i] - a[i + 1]);
        }
        else {
            b[i] = -1 * Abs(a[i] - a[i + 1]);
            c[i] = Abs(a[i] - a[i + 1]);
        }
    }
    for(int i = 1 ; i < n ; i++) {
        if(sum1 < 0) {
            sum1 = (ll)b[i];
        }
        else {
            sum1 += (ll)b[i];
        }
        MAX1 = max(MAX1 , sum1);
    }
    for(int i = 1 ; i < n ; i++) {
        if(sum2 < 0) {
            sum2 = (ll)c[i];
        }
        else {
            sum2 += (ll)c[i];
        }
        MAX2 = max(MAX2 , sum2);
    }
    printf("%I64d\n" , max(MAX1 , MAX2));
    return 0;
}