MKL普通矩阵运算示例及函数封装
本示例将介绍MKL中的矩阵乘法和求逆,使用MKL进行此类大型矩阵运算可大量节省计算时间和空间,但由于MKL中的原生API接口繁杂,因此将常用函数封装,便于后续使用,最后在实际例子中调用接口执行想要的矩阵运算。
1 MKL矩阵乘法案例
所用示例如下,矩阵A、B分别为
{\begin{array}{*{20}{c}}
1&{ - 1}
\end{array}}&{ - 3}&0&0\\
{\begin{array}{*{20}{c}}
{ - 2}&5
\end{array}}&0&0&0\\
{\begin{array}{*{20}{c}}
0&0
\end{array}}&4&6&4\\
{\begin{array}{*{20}{c}}
{\begin{array}{*{20}{l}}
{ - 4}\\
0\\
1
\end{array}}&{\begin{array}{*{20}{l}}
0\\
8\\
0
\end{array}}
\end{array}}&{\begin{array}{*{20}{l}}
2\\
0\\
0
\end{array}}&{\begin{array}{*{20}{l}}
7\\
0\\
0
\end{array}}&{\begin{array}{*{20}{l}}
0\\
{ - 5}\\
0
\end{array}}
\end{array}} \right]_{6 \times 5}}{\begin{array}{*{20}{c}}
{}&{B = \left[ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
1\\
{ - 2}
\end{array}}&{\begin{array}{*{20}{c}}
{ - 1}\\
5
\end{array}}&{\begin{array}{*{20}{c}}
{ - 3}\\
0
\end{array}}&{\begin{array}{*{20}{c}}
0\\
0
\end{array}}\\
0&0&4&6\\
{ - 4}&0&2&7\\
0&8&0&0
\end{array}} \right]}
\end{array}_{5 \times 4}}
\]
(1)matlab计算结果
作为标准答案,验证后续调用的正确性。
A=[1,-1,-3,0,0;
-2,5,0,0,0;
0,0,4,6,4;
-4,0,2,7,0;
0,8,0,0,-5;
1,0,0,0,0];
B=[1,-1,-3,0;
-2,5,0,0;
0,0,4,6;
-4,0,2,7;
0,8,0,0];
A*B
输出为:
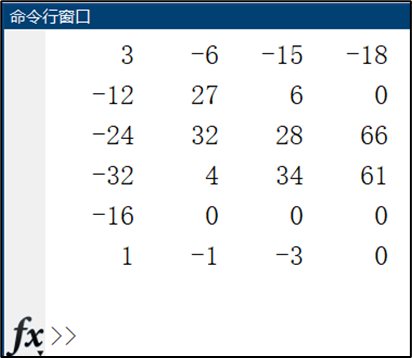
(2)MKL矩阵乘法
矩阵乘法接口
/*
输入:
MatrixA 矩阵A数据,类型为float型的二维数组
rowA 矩阵A的行数
colA 矩阵A的列数
MatrixB 矩阵B数据,类型为float型的二维数组
colC 矩阵C的列数
allocType 二维矩阵定义方式,
allocType=0时,定义为A=alloc(row,col), A[col][row](第一维表示列,第二维表示行)
allocType=1时,定义为A=alloc(col,row), A[row][col](第一维表示行,第二维表示列)
输出:
MatrixC 矩阵A*B数据,类型为float型的二维数组,为矩阵乘法计算结果
*/
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC, int allocType);
函数代码
函数将使用MKL库中的矩阵乘法接口cblas_?gemm实现,具体用法及参数详解见MKL库矩阵乘法(cblas_?gemm) - GeoFXR - 博客园 (cnblogs.com)
#include "MKL_Matrix_Methods.h"
//矩阵乘法
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC, int allocType) {
if (MatrixA == NULL) {
return false;
}
if (MatrixB == NULL) {
return false;
}
if (MatrixC == NULL) {
return false;
}
int M, N, K;
int lda, ldb, ldc;
M = rowsA;
N = colsA;
K = colsC;
float *A = NULL;
float *B = NULL;
float *C = NULL;
//由于mkl的矩阵乘法函数仅支持一维数组,需对输入进行转换
A = (float*)mkl_malloc(M*N * sizeof(float), 64);
B = (float*)mkl_malloc(N*K * sizeof(float), 64);
C = (float*)mkl_malloc(M*K * sizeof(float), 64);
if (A == NULL || B == NULL || C == NULL) {
mkl_free(A);
mkl_free(B);
mkl_free(C);
return false;
}
//赋值
int i = 0;
int j = 0;
//如果alloc是行在前列在后
if (allocType == 0) {
lda = M;
ldb = N;
ldc = M;
for (i = 0; i < N; i++) {
memcpy(A + i * M, MatrixA[i], M * sizeof(float));
}
for (i = 0; i < K; i++) {
memcpy(B + i * N, MatrixB[i], N * sizeof(float));
}
cblas_sgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A,
lda, B, ldb, 0, C, ldc);
for (i = 0; i < K; i++) {
memcpy(MatrixC[i], C + i * M, M * sizeof(float));
}
}
//如果alloc是列在前行在后
else {
lda = N;
ldb = K;
ldc = K;
for (i = 0; i < M; i++) {
memcpy(A + i * N, MatrixA[i], N * sizeof(float));
}
for (i = 0; i < N; i++) {
memcpy(B + i * K, MatrixB[i], K * sizeof(float));
}
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A, lda, B, ldb,
0, C, ldc);
for (i = 0; i < M; i++) {
memcpy(MatrixC[i], C + i * K, K * sizeof(float));
}
}
}
在执行main.cpp中的MKL_MatrixMul_Demo()之后,
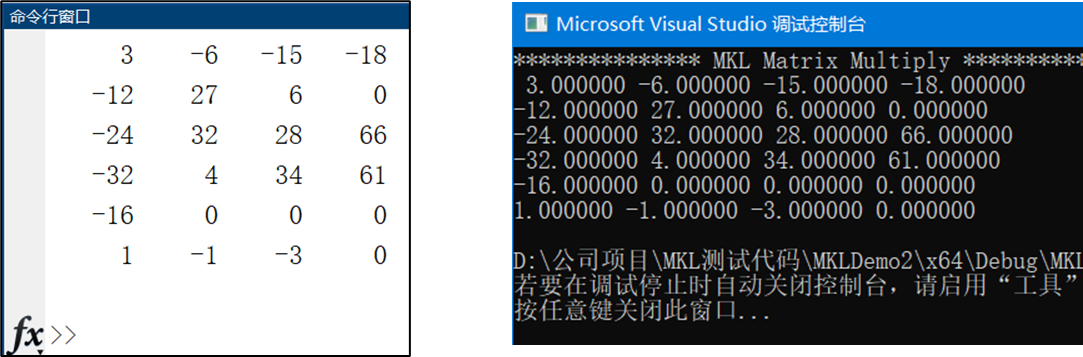
结果与matlab一致。
2 MKL矩阵求逆案例
(1)matlab计算结果
作为标准答案,验证后续调用的正确性。
A = [1 2 4 0 0;
2 2 0 0 0;
4 0 3 0 0;
0 0 0 4 0;
0 0 0 0 5];
A_inv = inv(A)
输出为:

(2)MKL求逆
矩阵求逆接口
/*
函数功能:基于MKL库的矩阵求逆
输入:
Matrix 输入矩阵Matrix,n行n列
n 矩阵的行、列数
输出:
Matrix Matrix 的逆,n行n列
*/
bool MKL_MatrixInverse(float**Matrix, int n)
函数代码
使用MKL中的LAPACK库计算线性方程组\(AX=B\)的解,当\(B\)为单位阵时,\(X\)即为\(A\)的逆矩阵\(A^{-1}\)。函数使用的接口为LAPACKE_sgesv,具体参数详解见MKL库线性方程组求解(LAPACKE_?gesv) - GeoFXR - 博客园 (cnblogs.com)
bool MKL_MatrixInverse(float**Matrix, int n) {
MKL_INT nrhs = n, lda = n, ldb = n;
// 创建置换矩阵,长度为n的数组
int *ipiv = (int*)mkl_malloc(n * sizeof(int), 64);
if (ipiv == NULL) {
return false;
}
// 创建MKL矩阵
float *matA = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matA == NULL) {
return false;
}
//将二维数组转换为一维MKL数组
for (int i = 0; i < n; i++) {
memcpy(matA + i * n, Matrix[i], n * sizeof(float));
}
// 创建一个单位阵B
float *matEye = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matEye == NULL) {
return false;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matEye[i * n + j] = (i == j) ? 1.0 : 0.0;
}
}
// 调用求解AX=B函数
LAPACKE_sgesv(LAPACK_ROW_MAJOR, n, nrhs, matA, lda, ipiv, matEye, ldb);
// 将MKL矩阵转换回普通二维数组
for (int i = 0; i < n; i++) {
memcpy(Matrix[i], matEye + i * n, n * sizeof(float));
}
// 释放内存
mkl_free(matA);
mkl_free(ipiv);
mkl_free(matEye);
return true;
}
在执行main.cpp中的MKL_MatrixInverse_Demo()之后,
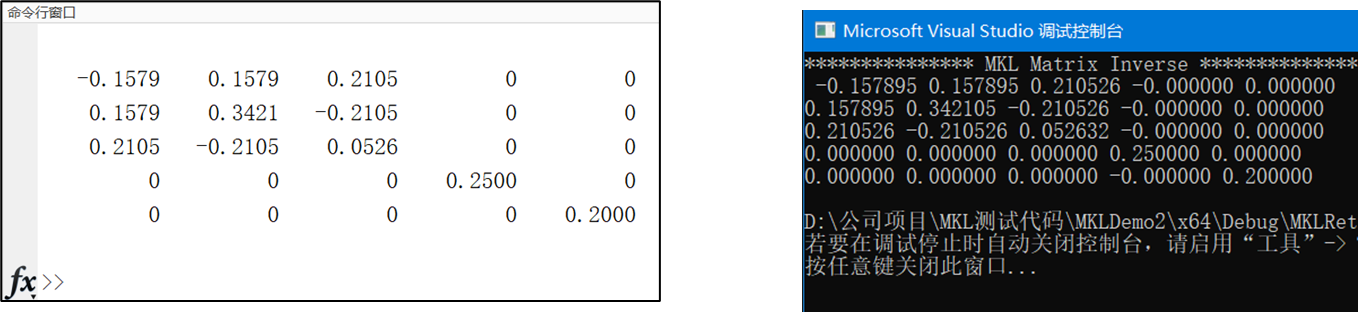
结果与matlab一致。
完整代码
Ⅰ MKL_Matrix_Methods.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include"mkl.h"
#include "mkl_types.h"
#include"mkl_lapacke.h"
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC, int allocType);
bool MKL_MatrixInverse(float**Matrix, int n);
Ⅱ MKL_Matrix_Methods.cpp
#include "MKL_Matrix_Methods.h"
//矩阵乘法
bool MKL_MatrixMul(float **MatrixA, int rowsA, int colsA, float **MatrixB, int colsC, float **MatrixC, int allocType) {
if (MatrixA == NULL) {
return false;
}
if (MatrixB == NULL) {
return false;
}
if (MatrixC == NULL) {
return false;
}
int M, N, K;
int lda, ldb, ldc;
M = rowsA;
N = colsA;
K = colsC;
float *A = NULL;
float *B = NULL;
float *C = NULL;
//由于mkl的矩阵乘法函数仅支持一维数组,需对输入进行转换
A = (float*)mkl_malloc(M*N * sizeof(float), 64);
B = (float*)mkl_malloc(N*K * sizeof(float), 64);
C = (float*)mkl_malloc(M*K * sizeof(float), 64);
if (A == NULL || B == NULL || C == NULL) {
mkl_free(A);
mkl_free(B);
mkl_free(C);
return false;
}
//赋值
int i = 0;
int j = 0;
//如果alloc是行在前列在后
if (allocType == 0) {
lda = M;
ldb = N;
ldc = M;
for (i = 0; i < N; i++) {
memcpy(A + i * M, MatrixA[i], M * sizeof(float));
}
for (i = 0; i < K; i++) {
memcpy(B + i * N, MatrixB[i], N * sizeof(float));
}
cblas_sgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A,
lda, B, ldb, 0, C, ldc);
for (i = 0; i < K; i++) {
memcpy(MatrixC[i], C + i * M, M * sizeof(float));
}
}
//如果alloc是列在前行在后
else {
lda = N;
ldb = K;
ldc = K;
for (i = 0; i < M; i++) {
memcpy(A + i * N, MatrixA[i], N * sizeof(float));
}
for (i = 0; i < N; i++) {
memcpy(B + i * K, MatrixB[i], K * sizeof(float));
}
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, M, K, N, 1, A, lda, B, ldb,
0, C, ldc);
for (i = 0; i < M; i++) {
memcpy(MatrixC[i], C + i * K, K * sizeof(float));
}
}
}
//矩阵求逆
bool MKL_MatrixInverse(float**Matrix, int n) {
MKL_INT nrhs = n, lda = n, ldb = n;
// 创建置换矩阵,长度为n的数组
int *ipiv = (int*)mkl_malloc(n * sizeof(int), 64);
if (ipiv == NULL) {
return false;
}
// 创建MKL矩阵
float *matA = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matA == NULL) {
return false;
}
//将二维数组转换为一维MKL数组
for (int i = 0; i < n; i++) {
memcpy(matA + i * n, Matrix[i], n * sizeof(float));
}
// 创建一个单位阵B
float *matEye = (float *)mkl_malloc(n * n * sizeof(float), 64);
if (matEye == NULL) {
return false;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matEye[i * n + j] = (i == j) ? 1.0 : 0.0;
}
}
// 调用求解AX=B函数
LAPACKE_sgesv(LAPACK_ROW_MAJOR, n, nrhs, matA, lda, ipiv, matEye, ldb);
// 将MKL矩阵转换回普通二维数组
for (int i = 0; i < n; i++) {
memcpy(Matrix[i], matEye + i * n, n * sizeof(float));
}
// 释放内存
mkl_free(matA);
mkl_free(ipiv);
mkl_free(matEye);
return true;
}
Ⅲ main.cpp
#include "MKL_Matrix_Methods.h"
#include "alloc.h"
#define M 6
#define N 5
#define K 4
void MKL_MatrixMul_Demo();
void MKL_MatrixInverse_Demo();
int main()
{
MKL_MatrixMul_Demo(); //矩阵乘法示例
MKL_MatrixInverse_Demo(); //矩阵求逆示例
}
//矩阵乘法
void MKL_MatrixMul_Demo() {
int rowsA = M, colsA = N;
int rowsB = N, colsB = K;
int rowsC = M, colsC = K;
float Atemp[M][N] = {
{1,-1,-3,0,0},
{-2,5,0,0,0},
{0,0,4,6,4},
{-4,0,2,7,0},
{0,8,0,0,-5},
{1,0,0,0,0},
};
float Btemp[N][K] = {
{1,-1,-3,0},
{-2,5,0,0},
{0,0,4,6},
{-4,0,2,7},
{0,8,0,0}
};
int allocType = 1; //alloc2(col,row)列在前,行在后
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
float **matrixB = alloc2float(colsB, rowsB);
memset(matrixB[0], 0, rowsB*colsB * sizeof(float));
memcpy(matrixB[0], Btemp, rowsB*colsB * sizeof(float));
float **matrixC = alloc2float(colsC, rowsC);
memset(matrixC[0], 0, rowsC*colsC * sizeof(float));
MKL_MatrixMul(matrixA, rowsA, colsA, matrixB, colsC, matrixC,1); //调用MKL矩阵乘法接口
/* 输出结果 */
printf("*************** MKL Matrix Multiply ***************\n ");
for (int i = 0; i < rowsC; i++) {
for (int j = 0; j < colsC; j++) {
printf("%f ", matrixC[i][j]);
}
printf("\n");
}
free(matrixA);
free(matrixB);
free(matrixC);
}
// 矩阵求逆
void MKL_MatrixInverse_Demo() {
int rowsA = N, colsA = N;
float Atemp[N][N] = {
{1,2,4,0,0},
{2,2,0,0,0},
{4,0,3,0,0},
{0,0,0,4,0},
{0,0,0,0,5}
};
//将一般二维数组转换为alloc表示
float **matrixA = alloc2float(colsA, rowsA);
memset(matrixA[0], 0, rowsA*colsA * sizeof(float));
//复制二维数组到二级指针
memcpy(matrixA[0], Atemp, rowsA*colsA * sizeof(float));
//求逆
MKL_MatrixInverse(matrixA, rowsA);
/* 输出结果 */
printf("*************** MKL Matrix Inverse ***************\n ");
for (int i = 0; i < rowsA; i++) {
for (int j = 0; j < colsA; j++) {
printf("%f ", matrixA[j][i]);
}
printf("\n");
}
free(matrixA);
}
MKL普通矩阵运算示例及函数封装的更多相关文章
- MKL稀疏矩阵运算示例及函数封装
Intel MKL库提供了大量优化程度高.效率快的稀疏矩阵算法,使用MKL库的将大型矩阵进行稀疏表示后,利用稀疏矩阵运算可大量节省计算时间和空间,但由于MKL中的原生API接口繁杂,因此将常用函数封装 ...
- NFC(9)NDEF文本格式规范及读写示例(解析与封装ndef 文本)
只有遵守NDEF文本格式规范的数据才能写到nfc标签上. NDEF文本格式规范 不管什么格式的数据本质上都是由一些字节组成的.对于NDEF文本格式来说. 1,这些数据的第1个字节描述了数据的状态, 2 ...
- c#读写共享内存操作函数封装
原文 c#读写共享内存操作函数封装 c#共享内存操作相对c++共享内存操作来说原理是一样,但是c#会显得有点复杂. 现把昨天封装的读写共享内存封装的函数记录下来,一方面希望给需要这块的有点帮助,另一方 ...
- [妙味JS基础]第九课:定时器管理、函数封装
知识点总结 函数封装 回调函数 实例:抖动函数 获取当前的位置 通过数组来实现,一正一负,直到恢复成0为止. 当前位置与数组中各值相加
- 前端总结·基础篇·JS(三)arguments、callee、call、apply、bind及函数封装和构造函数
前端总结系列 前端总结·基础篇·CSS(一)布局 前端总结·基础篇·CSS(二)视觉 前端总结·基础篇·CSS(三)补充 前端总结·基础篇·JS(一)原型.原型链.构造函数和字符串(String) 前 ...
- XMLHttpRequest函数封装
XMLHttpRequest函数封装: function ajax(Url,sccuessFn,failureFn) { //1.创建XMLHttpRequest对象 var xhr = null; ...
- Appium python自动化测试系列之滑动函数封装实战(八)
8.1 什么是函数的封装 教科书上函数的封装太官方,我们这里暂且将函数的封装就是为了偷懒把一些有共性的功能或者一些经常用的功能以及模块放在一起,方便我们以后再其他地方调用.这个只是个人的理解所以大家懂 ...
- c++ 回调函数封装
std::function<void(int a,int b)> ha; //函数封装 当成参数用callback std::bind(&fun1,this,std::plac ...
- 定时器中的this和函数封装的简单理解;
一.定时器中的this: 不管定时器中的函数怎么写,它里面的this都是window: 在函数前面讲this赋值给一个变量,函数内使用这个变量就可以改变this的指向 二.函数封装 函数封装是一种函数 ...
- JS中深浅拷贝 函数封装代码
一.了解 基本数据类型保存在栈内存中,按值访问,引用数据类型保存在堆内存中,按址访问. 二.浅拷贝 浅拷贝只是复制了指向某个对象的指针,而不是复制对象本身,新旧对象其实是同一内存地址的数据,修改其中一 ...
随机推荐
- 【虚拟机】在VMware中为Ubuntu虚拟机设置共享文件夹
[虚拟机]在VMware中为Ubuntu虚拟机设置共享文件夹 零.需求 有些开发工具在Windows上没有,只能在Ubuntu上开发,但是自己电脑是Windows的,开发完成后需要通过Windows分 ...
- Oracle PLSQL 存储过程无法进入单步调试
使用PLSQL工具调试存储过程的时候,不管你怎么设置断点,当你点击测试的时候就瞬间执行而过你无法进入单步调试 解决办法:
- FastAPI依赖注入系统及调试技巧
title: FastAPI依赖注入系统及调试技巧 date: 2025/04/11 15:00:50 updated: 2025/04/11 15:00:50 author: cmdragon ex ...
- 一文速通 Python 并行计算:07 Python 多线程编程-线程池的使用和多线程的性能评估
一文速通 Python 并行计算:07 Python 多线程编程-线程池的使用和多线程的性能评估 摘要: 本文介绍了 Python 线程池(ThreadPoolExecutor)的使用方法,包括线程池 ...
- 关于:js使用$.parseJSON字符串转json对象报错Uncaught SyntaxError- Unexpected token o in JSON at position 1
今天使用js使用$.parseJSON字符串转json对象报错Uncaught SyntaxError- Unexpected token o in JSON at position 1,一直找不到原 ...
- CF1370C题解
本蒟蒻的第二篇题解,找题归功于教练 题目传送门 这道题目找好了规律很简单: 具体思路: 题目大意: 有一个正整数 nnn.两名玩家轮流操作.每次操作可以执行以下一种: 将 nnn 除以一个 nnn 的 ...
- Linux各种服务配置开机自启
一.Linux配置redis开机自启 (1)到redis配置文件中找到conf文件:vi redis.conf (2)daemonize no 修改为:daemonize yes (3)cd /etc ...
- jdbc写一个访问数据库的工具类
操作的工具类 package com.zjw.jdbc2; /** * jdbc操作的工具类 * @author Administrator * */ import java.sql.Connecti ...
- 校园圈子系统:Uni-app跨端渲染+TP6实时推送核心逻辑与代码
在TP6中实现实时推送功能,核心逻辑围绕WebSocket服务搭建.用户连接管理.消息路由和性能优化展开.以下是详细的实现步骤和逻辑说明: TP6实时推送核心逻辑 WebSocket服务搭建 使用Wo ...
- LLM主要架构
LLM本身基于Transformer架构 自2017年,Attention is all you need诞生起,原始的Transformer模型不同领域的模型提供了灵感和启发 基于原始的Transf ...
