P5987 [PA2019] Terytoria / 2023NOIP A层联测13 T3 全球覆盖

P5987 [PA2019] Terytoria / 2023NOIP A层联测13 T3 全球覆盖

题面及数据范围

对于一个点对，可以降维为线段，转化为 1 维的问题。

如图：

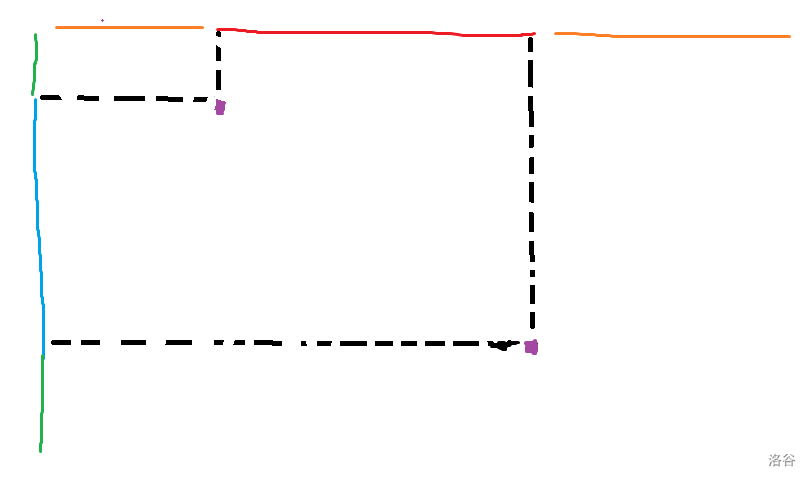
我们可以在横着的方向和竖着的方向个选择一种颜色的线段，任意一种选择可以构成一个合法的矩形。

我们需要求最大重叠面积，可以转化为两个一维的求最大公共线段交的问题，最后将答案相乘即为原问题。（横着选和竖着选互不干扰）

一维的问题为：

在数轴上有若干条线段，线段有一个起点和一个终点，选择这条线段或选择这条线段的补集，求最大公共交集。

先分析线段数小于 64 的情况。

我们给每一条线段左端点和右端点一个相同的值 val，val 为 2 的整数次方且每个 val 各不相同。

如图：

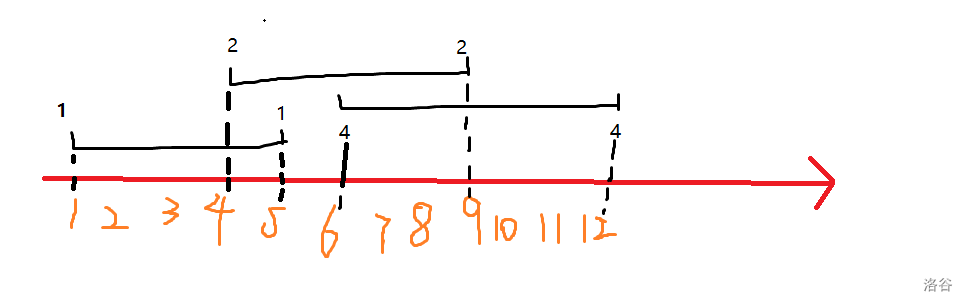
f[i] 为取到第 i 个点的选择情况，f[i]=f[i-1]\bigoplus val[i]。

如果 f[i] 中第 i 位为 1 表示需要选这条线段才可以选这个点。

求相同 f[i] 的点有多少即可。

如果大于 64 我们无法给每个线段分配唯一的 val 值，我们可以在 [0,2^{64}] 中随机一个数作为 val 值。

尽管可能有错误，不过根据生日悖论正确率高达 99.9936\%。

CODE

 #include<bits/stdc++.h>
 using namespace std;
 ​
 #define ull unsigned long long
 #define int long long
 #define piu pair<int,ull>
 ​
 mt19937_64 rnd(random_device{}());
 ​
 const int maxn=1e6+5;
 ​
 int n,x,y;
 int a[2][maxn];
 ​
 piu b[maxn];
 ​
 int sv(int *a,int X)
 {
     for(int i=0;i<n;i+=2)
     {
         ull v=rnd();
         b[i]=make_pair(a[i],v);
         b[i+1]=make_pair(a[i+1],v);
     }
     ull now=0;sort(b,b+n);
     unordered_map<ull,int>mp;
     b[n].first=X;
     mp[0]=b[0].first;
     for(int i=0;i<n;i++)
     {
         now^=b[i].second;mp[now]+=b[i+1].first-b[i].first;
     }
     int ans=0;
     for(auto v:mp) ans=max(ans,v.second);
     return ans;
 }
 ​
 signed main()
 {
     scanf("%lld%lld%lld",&n,&x,&y);
     n<<=1;
     for(int i=0;i<n;i++) for(int j=0;j<2;j++) scanf("%lld",&a[j][i]);
     printf("%lld",sv(a[0],x)*sv(a[1],y));
 }