U559607 简短的题目-二分+st表

单调性证明：

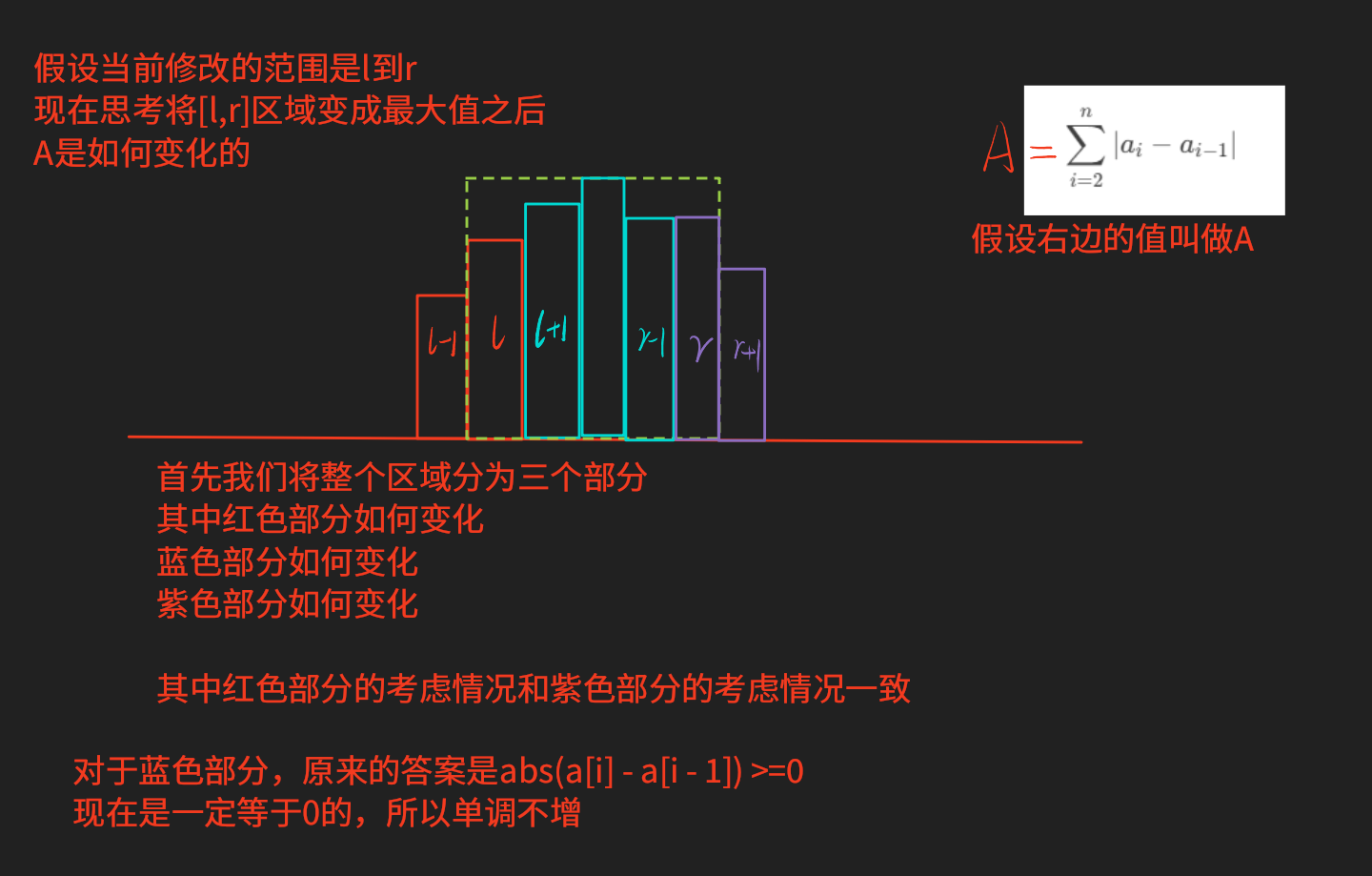
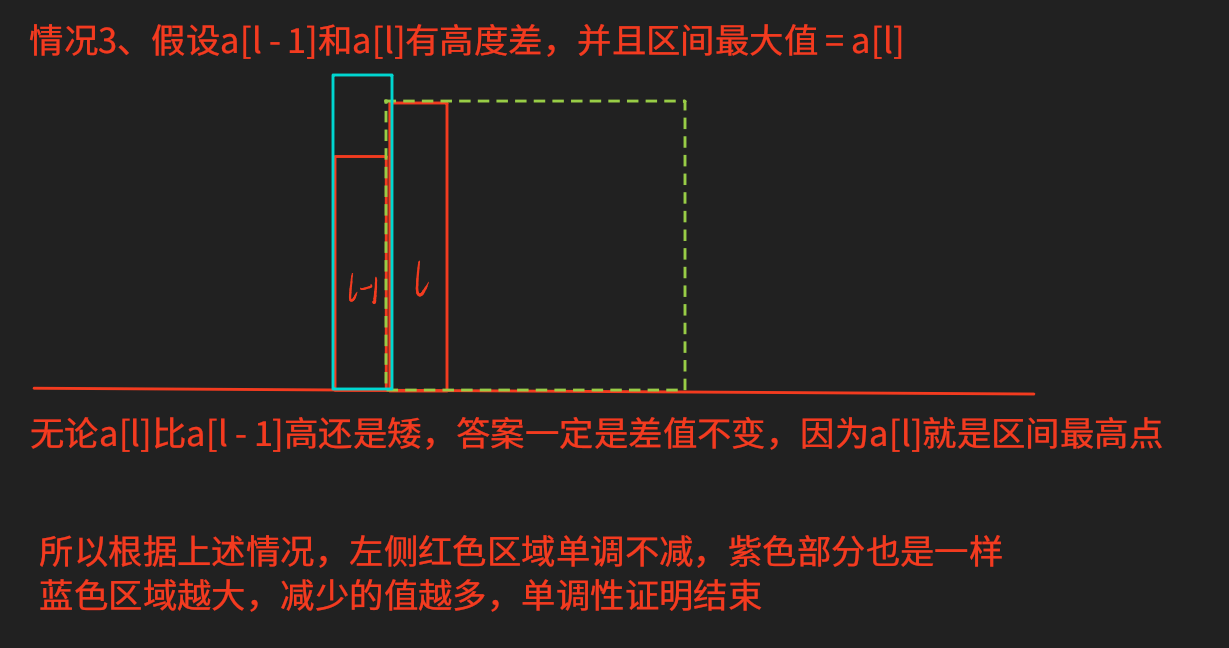
对于小数据范围，可以直接考虑暴力枚举长度的方式。

对于额外的 \(20 \%\) 的数据范围，所有的差值加起来肯定是小于等于 \(10 ^ 9\) ，所以不需要操作，直接输出 \(0\) 即可。

对于 \(100 \%\) 的数据范围，在原来的基础上，思考优化的方式，比如中间过程求解最值可以用 \(st\) 表来实现，

另外可以观察得到，长度越长，此时的数组权值越小，越容易满足题目要求。

所以二分答案长度，小的长度可以满足，大的长度一定可以满足。

关键是 \(check\) 函数的写法，在此处，我们可以考虑枚举不同的左端点，然后计算对应的右端点，

这一段区间 \([i, i + m - 1]\) 都变成了最值，此时这段区间的权值直接变成 \(0\) ，

此时考虑端点 \(i - 1\) 和 \(i + m\) 的答案也发生了变化，直接单点进行修改，

减去原来的，加上新增的即可。