笔记-AM的正交解调法

1.AM的模拟调制过程

​ AM信号是一种振幅调制信号，其携带的信息保存在其信号的振幅中，通过改变载波的振幅来实现基带数据的传输。

其函数表达式如下：

\[s(t) = (A + m(t))*cos(2\pi ft + \varphi)
\]

其中：

A:表示基带信号加载的直流分量。

m(t):表示基带信号。

\(cos(2\pi ft + \varphi )\):表示载波信号。

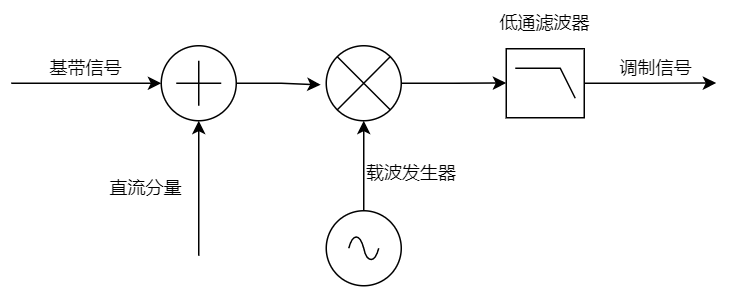
正交调制法公式如下：

\[I(t) = (A + m(t))*cos(\varphi) \\
Q(t) = (A + m(t))*sin(\varphi) \\
s(t) = I(t)*cos(2\pi ft) + Q(t)*sin(2\pi ft)
\]

2.AM的数字解调

​ AM解调的方法有很多种，以下只简单介绍两种，分别为非相干解调（包络面解调法）和相干解调（正交解调法）。一般的相干解调法要求产生一个与调制载波严格等频等相的载波用于信号的解调，抗载频失配能力较差，毕竟出现频差或者相差就会对解调出来的信号产生较大的误差。

​ 以下介绍的正交解调法将消除频差或者相差带来的误差，增加其解码正确率。

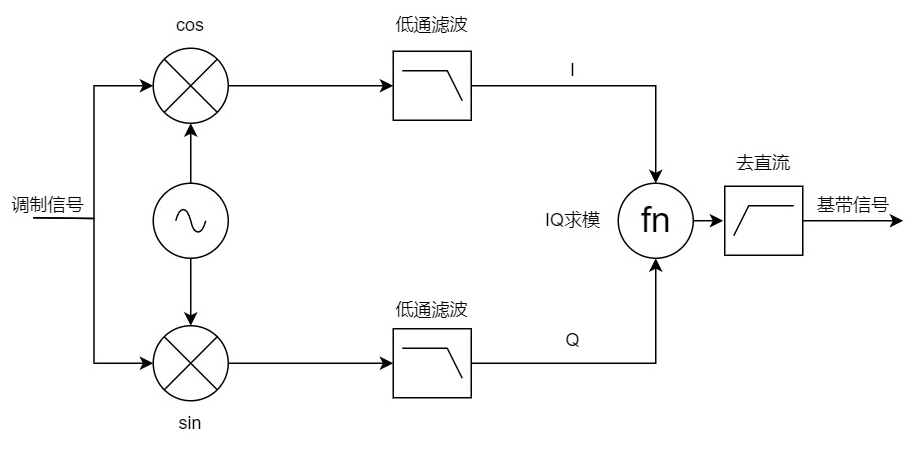
通过正交的方式即可解调出基带信号，其数学推导如下：

​ 假设基带信号频率为f1,调制的载波频率为f2，直流信号为A,解调的载波频率为f3，则：

I路：

\[I(t) = s(t)*cos(2\pi f_3t + \varphi) = (A + cos(2\pi f_1t))*cos(2\pi f_2t) *cos(2\pi f_3t + \varphi)
\]

根据三角函数公式：

\[\begin{split}
I(t) &= \frac{1}{2}A[cos(2\pi (f_2 + f_3)t+\varphi) + cos(2\pi (f_2 - f_3)t+\varphi)] \\
&+ \frac{1}{4}[cos(2\pi (f_1 + f_2 + f_3)t+\varphi) + cos(2\pi (f_1 - f_2 - f_3)t+\varphi)] \\
&+ \frac{1}{4}[cos(2\pi (f_1 + f_2 - f_3)t+\varphi) + cos(2\pi (f_1 - f_2 + f_3)t+\varphi)]
\end{split}
\]

经过低通滤波器，不考虑滤波器增益：

\[I(t) = \frac{1}{2}Acos(2\pi (f_2 - f_3)t+\varphi) + \frac{1}{4}cos(2\pi (f_1 + f_2 - f_3)t+\varphi) + \frac{1}{4}cos(2\pi (f_1 - f_2 + f_3)t+\varphi)
\]

设解调的载波与调制的载波的频率偏移为f4：

\[f_4= f_3-f_2
\]

则：

\[I(t) = \frac{1}{2}Acos(2\pi f_4t+\varphi) + \frac{1}{4}cos(2\pi (f_1 + f_4)t+\varphi) + \frac{1}{4}cos(2\pi (f_1 - f_4)t+\varphi)
\]

同理可求得Q：

\[Q(t) = \frac{1}{2}Asin(2\pi f_4t+\varphi) + \frac{1}{4}sin(2\pi (f_1 + f_4)t+\varphi) + \frac{1}{4}sin(2\pi (f_1 - f_4)t+\varphi)
\]

还原信号：

\[s(t) = \sqrt{I(t)^2+Q(t)^2} = \frac{1}{2} (A + cos(2\pi f_1t))
\]

这样就消除了相位差带来的误差，同时这个有个前提：$$A + m(t)$$必须大于0，不过经过AM调制，一定是大于0的。否则将出现失真。

​ 由上式可以推断出解调的载波与调制的载波的频率偏移频率，只要位于设计的滤波器的带宽内，就可以解调出原始信号，与偏移量的大小无关。只要保证在获取I路信号和Q路信号的滤波器能正确将高频信号滤除，通过IQ求模，就可以成功将频差相位差两个变量消除。

3.去直流

​ 解调出来的信号中包含了一个直流信号A，在频谱分析中我们一般将直流信号当作频率为0的正弦信号，那么这样我们就可以通过滤波器的方式对直流进行处理。

1.均值滤波器

​ 将直流信号分量计算出来，将原信号减去直流信号就可以获取到基带信号。

\[m(t) = s(t) - A/2 = cos(2\pi f_1t)/2
\]

​ 均值滤波器表达式：

\[f(n) = \sum_{i=0}^{N-1} \frac{x(n+i)}{N}
\]

matlab：

close all;
N1 = 64;
N2 = 128;
N3 = 256;
a = ones(N1,1)/N1;
b = ones(N2,1)/N2;
c = ones(N3,1)/N3;
figure('menubar','figure');
[h1, w1] = freqz(a,1,2048,1000);
[h2, w2] = freqz(b,1,2048,1000);
[h3, w3] = freqz(c,1,2048,1000);
plot(w1, abs(h1),'DisplayName',num2str(N1));
hold on
plot(w2, abs(h2),'DisplayName',num2str(N2));
hold on
plot(w3, abs(h3),'DisplayName',num2str(N3));
title('Amplitude Response');
xlabel('Frequency (Hz)');
ylabel('Magnitude');
legend('show');

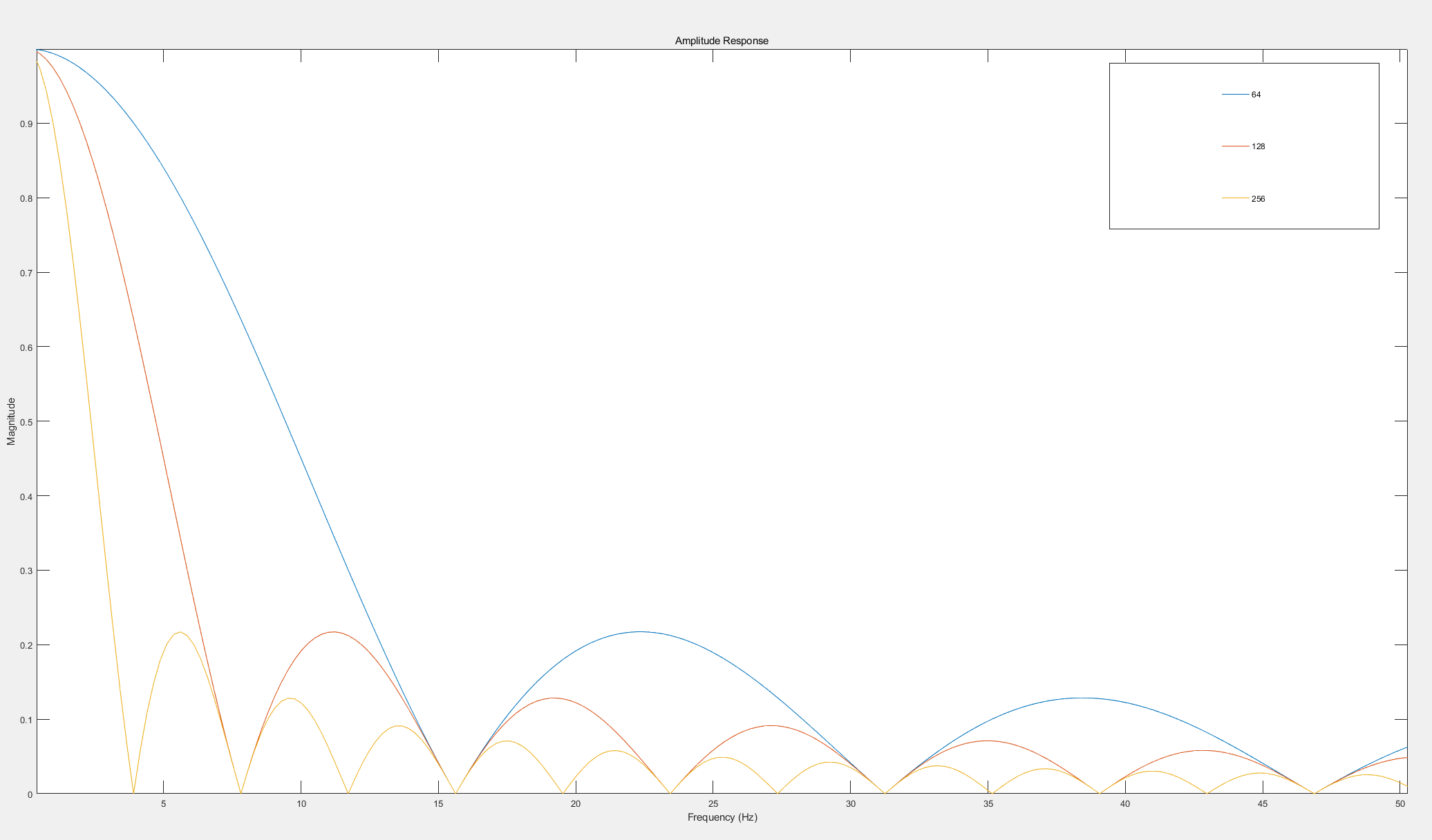
​ 可以看出均值滤波器实际上是一种特殊大的均值滤波器，随着N的变大，其截至频率变小。所以可以根据需求选择适当的截至频率，从而滤除除直流外的其余频率分量，从而分离出直流信号。

2.高通滤波器

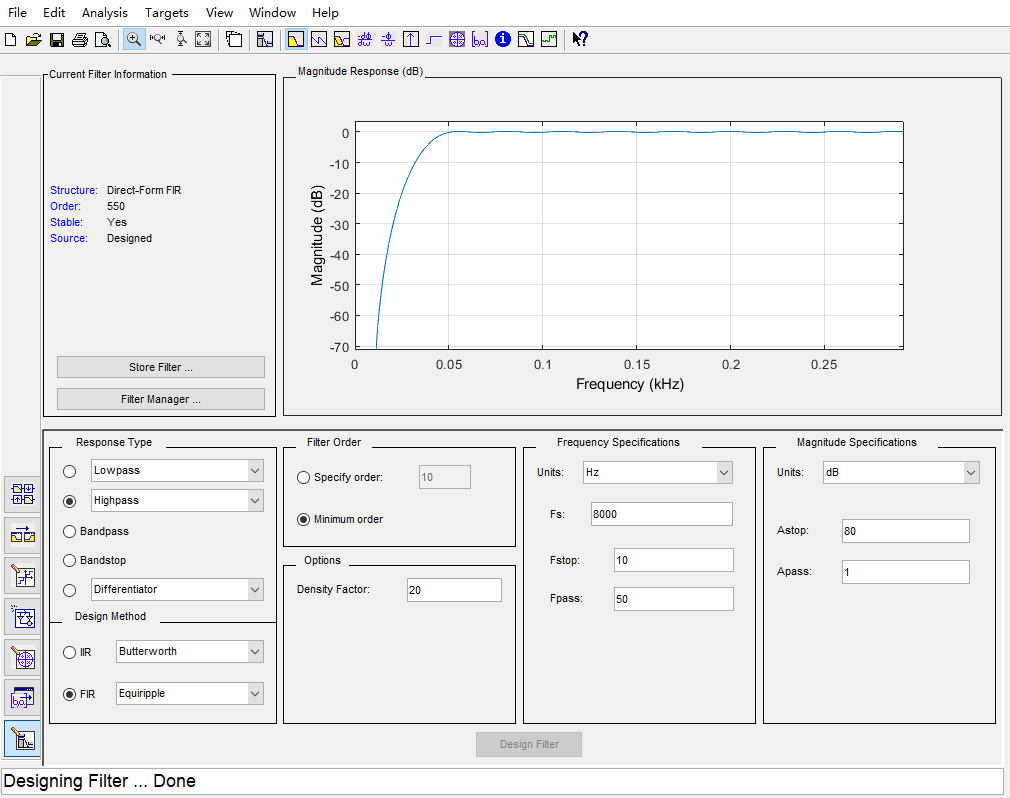
​ 均值滤波器采用分离出直流的方法来算出基带信号，高通滤波器则采样滤除直流信号，保留基带信号的方式来处理数据。可以通过matlab的工具filterDesigner来设计一个满足需求的高通滤波器。涉及要求，基带信号频率大于通带频率。且越靠近0频效果越好。

4.MATLAB解调

fs = 10E6;%采样率
A = 1;%直流大小
l = 1E3;%基带信号点数
f = 0.1E6;%基带信号
f_c = 2E6;%载波信号
t = 0:1/fs:(l-1)/fs;
fi = pi/3;%IQ相位
mt = cos(2*pi*f*t);%基带数据
%% IQ基带数据调制
I = (A + mt) * cos(fi);
Q = (A + mt) * sin(fi);
mod_data = I.* cos(2*pi*f_c*t) + Q.* sin(2*pi*f_c*t);

%% 基带数据解调
demod = sqrt(I.^2 + Q.^2)/2;

%% 去直流
dc_signal = sum(demod)/l;
demod0 = demod-dc_signal;
%% 保存IQ数据FPGA使用仿真
fid = fopen('AM.txt','w');
for i = 1:l
    fprintf(fid,'%d %d\n',floor(I(i)* (2^13)),floor(Q(i)* (2^13)));
end
fclose(fid);

%% 绘制
figure
time = 4;
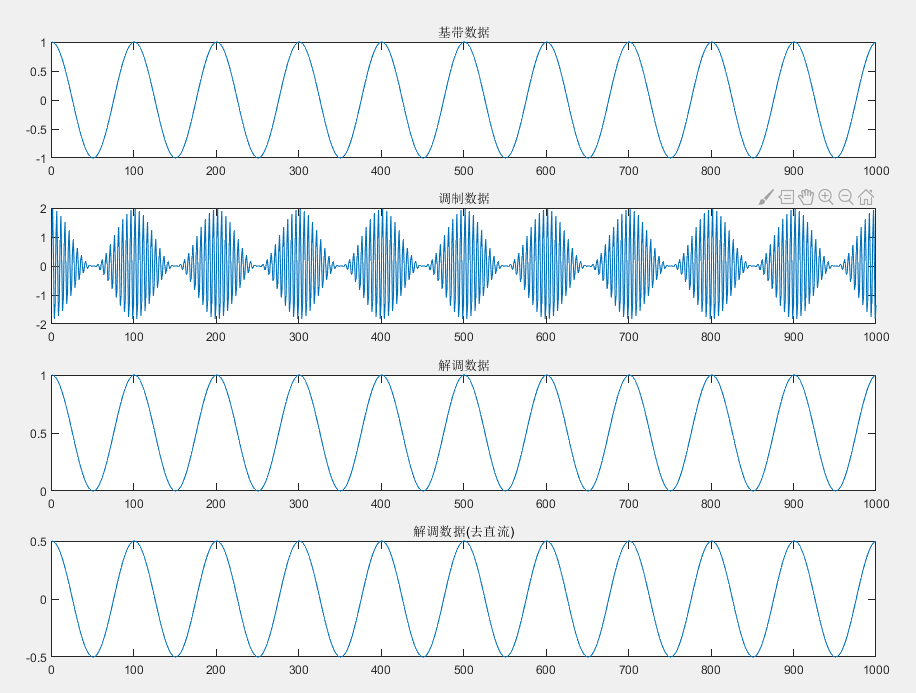
subplot(time,1,1);
plot(mt);
title('基带数据');

subplot(time,1,2);
plot(mod_data);
title('调制数据');

subplot(time,1,3);
plot(demod);
title('解调数据');

subplot(time,1,4);
plot(demod0);
title('解调数据(去直流)');

结果：

5.FPGA解调

逻辑代码：

module am_demod(
    input           clk             ,
    input           rst             ,
    //解调参数
    input           i_valid         ,
    input [15:0]    i_data_i        ,
    input [15:0]    i_data_q        ,
    output          o_rdy           ,
    output [15:0]   o_data    

)

    wire            am_valid          ;
    wire [23:0]     am_i              ;
    wire [23:0]     am_q              ;

    wire            am_rdy            ;
    wire [47 : 0]   m_axis_dout_tdata ;
    //AM 解调

    assign am_valid     = i_valid                        ;
    assign am_i         = {{8{i_data_i[15]}},i_data_i}   ;
    assign am_q         = {{8{i_data_q[15]}},i_data_q}   ;           

    cordic_translate cordic_translate (
        .aclk                     (clk                      ),                                        // input wire aclk
        .s_axis_cartesian_tvalid  (am_valid                 ),  // input wire s_axis_cartesian_tvalid
        .s_axis_cartesian_tdata   ({am_i,am_q}              ),    // input wire [47 : 0] s_axis_cartesian_tdata
        .m_axis_dout_tvalid       (am_rdy                   ),            // output wire m_axis_dout_tvalid
        .m_axis_dout_tdata        (m_axis_dout_tdata        )              // output wire [47 : 0] m_axis_dout_tdata
    );

    assign    o_rdy       = am_rdy                      ;
    assign    o_data      = m_axis_dout_tdata[15:0]     ;
endmodule

仿真代码：

module tb_am_demod();
    reg     clk;
    reg     rst;

    initial begin
        clk <= 0;
        rst <=   1;
        #300
        rst <= 0;
    end

    always #(100/2) clk  <=~clk;

    reg     valid;
    reg     [15:0]  din_i		;
    reg     [15:0]  din_q		;
    wire          	o_rdy     	;
    wire  	[15:0]  o_data  	;

am_demod   am_demod(
    .clk         	(clk		),
    .rst         	(rst		),

    .i_valid     	(valid		),
    .i_data_i    	(din_i		),
    .i_data_q    	(din_q		),
    .o_rdy          (o_rdy       ),
    .o_data         (o_data      )

);
    integer file_rd;                //定义数据读指针
    integer flag;
    initial begin                        //打开读取和写入的文件，这里的路径要对
        file_rd = $fopen("AM.txt","r");
    end
    reg     [15:0]  cnt;
    always @(posedge clk)begin
        if(rst)begin
            din_i   <= 0;
            din_q   <= 0;
            cnt     <= 0;
            valid   <= 0;
        end
        else if(cnt <= 1000)begin
            valid   <= 1;
            flag = $fscanf(file_rd,"%d %d",din_i,din_q);
            cnt <= cnt + 1;
        end
        else begin
            $fclose(file_rd);
            $stop();
        end
    end
endmodule

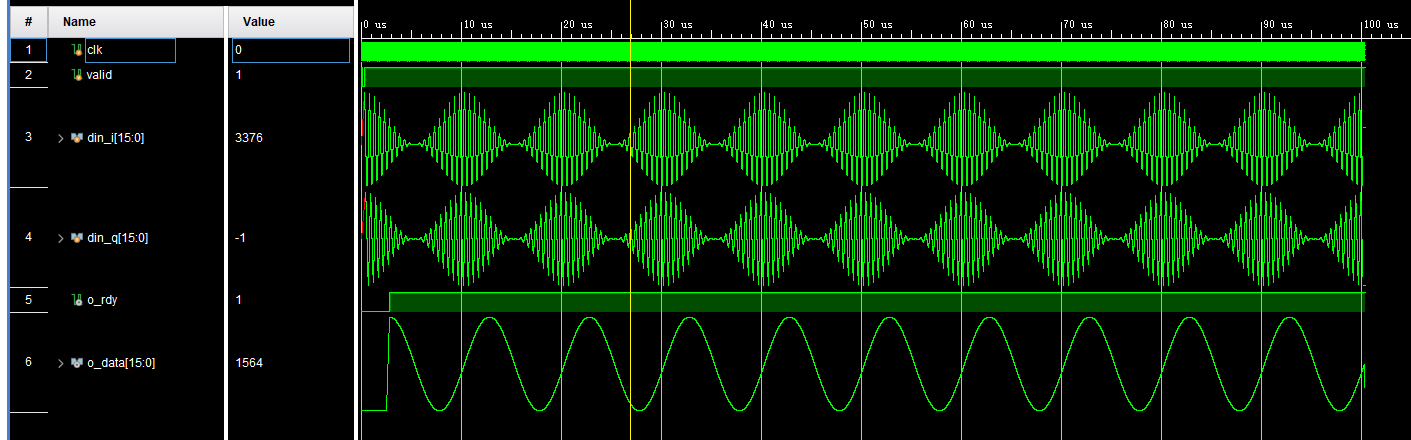
仿真结果：