浅谈压缩感知（二十）：OMP与压缩感知

主要内容：

OMP在稀疏分解与压缩感知中的异同
压缩感知通过OMP重构信号的唯一性

一、OMP在稀疏分解与压缩感知中的异同

、稀疏分解要解决的问题是在冗余字典(超完备字典)A中选出k列，用这k列的线性组合近似表达待稀疏分解信号y，可以用表示为y=Aθ，求θ。

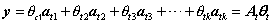
、压缩感知重构要解决的问题是事先存在一个θ和矩阵A，然后得到y=Aθ（压缩观测），现在是在已知y和A的情况下要重构θ。

A为M×N矩阵（M<<N，稀疏分解中为冗余字典，压缩感知中为传感矩阵A=ΦΨ，即测量矩阵Φ乘以稀疏矩阵Ψ），

y为M×1的列向量（稀疏分解中为待稀疏分解信号，压缩感知中为观测向量），

θ为N×1的列向量（稀疏分解中为待求分解系数，压缩感知中为信号x的在变换域Ψ的系数，x=Ψθ）。

相同点：

对已知y和A的情况下，求y=Aθ中的θ。
稀疏分解中θ是稀疏的，在压缩感知中信号也需要满足稀疏性的条件，这也是相同点之一。（OMP一开始在应用在稀疏表示上，后来压缩感知恰好信号也满足稀疏性条件，因此OMP也适用于压缩感知问题）

不同点：

在稀疏分解中θ是事先不存在的，我们要去求一个θ用Aθ近似表示y，求出的θ并不能说对与错；在压缩感知中，θ是事先存在的，只是现在不知道，我们要通过某种方法如OMP去把θ求出来，求出的θ应该等于原先的θ的，然后可求原信号x=Ψθ。

压缩感知中的A需要满足一定的条件来保证重建的可行性与唯一性。（如RIP、spark等）

二、压缩感知通过OMP重构信号的唯一性

问题：

通过OMP等重构算法求出的θ就是原来的x=Ψθ中的那个θ吗？为什么通过OMP迭代后一定会选出矩阵A的那几列呢？会不会选择A的另外几列，它们的线性组合也满足y=Aθ？

证明：

思路与证明spark常数一致。浅谈压缩感知（十五）：感知矩阵之spark常数

压缩感知的前提条件：若要恢复y=Aθ中k稀疏的θ，要求感知矩阵A（感知矩阵A=ΦΨ，即测量矩阵Φ乘以稀疏矩阵Ψ）至少任意2k列线性相关。这是压缩感知中A必须满足的一个条件。

假设通过OMP迭代后，存在两种不同的线性组合满足y=Aθ

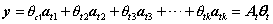
即A_tθ_t=A_rθ_r_，这意味着Aθ_k1= Aθ_k2_，即A (θ_k1－θ_k2)=0。此处的θ大小与y一致，但只有与选中对应列的位置处不为0.

两个k稀疏的N维信号（长度为N的列向量）θk1和θk2，它们的差向量(θk1－θk2)的稀疏度最大不超过2k，（当θk1和θk2中的非零项都没有对应在同一位置时）。

而A必须满足至少任意2K列线性相关，因此A的零空间维度必须至少为2K，而(θk1－θk2)的稀疏度最大不超过2k，因此A (θk1－θk2)=0并不成立，即原假设不成立。

所以在感知矩阵A满足至少任意2k列线性相关的前提下（即spark常数），通过OMP算法恢复出的θ是唯一的。

三、参考文章

http://blog.csdn.net/jbb0523/article/details/45100659

http://blog.csdn.net/jbb0523/article/details/45102383