Codeforces 868D Huge Strings - 位运算 - 暴力

You are given n strings s1, s2, ..., sn consisting of characters 0 and 1. m operations are performed, on each of them you concatenate two existing strings into a new one. On the i-th operation the concatenation saisbi is saved into a new string sn + i (the operations are numbered starting from 1). After each operation you need to find the maximum positive integer k such that all possible strings consisting of 0 and 1 of length k (there are 2k such strings) are substrings of the new string. If there is no such k, print 0.

Input

The first line contains single integer n (1 ≤ n ≤ 100) — the number of strings. The next n lines contain strings s1, s2, ..., sn (1 ≤ |si| ≤ 100), one per line. The total length of strings is not greater than 100.

The next line contains single integer m (1 ≤ m ≤ 100) — the number of operations. m lines follow, each of them contains two integers aiabd bi (1 ≤ ai, bi ≤ n + i - 1) — the number of strings that are concatenated to form sn + i.

Output

Print m lines, each should contain one integer — the answer to the question after the corresponding operation.

Example

input

5
01
10
101
11111
0
3
1 2
6 5
4 4

output

1
2
0

Note

On the first operation, a new string "0110" is created. For k = 1 the two possible binary strings of length k are "0" and "1", they are substrings of the new string. For k = 2 and greater there exist strings of length k that do not appear in this string (for k = 2 such string is "00"). So the answer is 1.

On the second operation the string "01100" is created. Now all strings of length k = 2 are present.

On the third operation the string "1111111111" is created. There is no zero, so the answer is 0.

---

　　题目大意 有n个01字符串，第i个操作是生成第n + i个字符串，方式是将两个已经存在的字符串拼接到一起，然后询问最大的k使得所有长度为k的01串都在这个串中出现过。

　　范围很吓人，意味着最大可能你需要判断2¹⁰⁰个串是否存在(和同学组队开黑的时候被吓坏了。。懵逼了好久。)，然而事实上。。答案都非常小。至少我没有找到一个超过10的。

　　另外注意到是拼接，所以串内部的情况不变，唯一增加新出现的子串的地方是拼接处，因为已经知道答案很小，就直接暴力就好了。

　　另外注意一个细节，就是用位运算弄得时候记得在开头加一个1，不然它会认为01和001是同一个串，但是101中并不存在串001。

　　(个人认为这道题的难点就在于估计答案范围，猜到很小就乱搞就好了，方法很多，什么记忆化搜索+二分也可以)

　　下面是答案会比较小的证明:(感谢我的学长idy002)

　　考虑长度为k的01串，在两个串进行合并的时候，两个串内部包含的本质不同的串是不变的，所以不会增加。因此新增加的子串一定是跨过交界处。

　　所以最多有(k - 1)个新增的本质不同的01串。再加上原本的包含为k的本质不同的01串的个数，可以列得不等式:

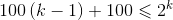
　　解不等式得到k不会超过11。

Code

 /**
  * Codeforces
  * Problem#868D
  * Accepted
  * Time: 30ms
  * Memory: 1700k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 #define limlen 15

 typedef class String {
     public:
         string pre, suf;
         boolean overflow;
         int rt;
         bitset<> mark;

         String():overflow(false) {        }
 }String;

 String operator + (String& a, String& b) {
     String rt;
     rt.overflow = a.overflow || b.overflow;
     rt.mark = a.mark | b.mark;
     if(!a.overflow) {
         rt.pre = a.pre + b.pre;
         if(rt.pre.length() > limlen)
             rt.overflow = true, rt.pre.resize(limlen);
     } else rt.pre = a.pre;
     if(!b.overflow) {
         rt.suf = a.suf + b.suf;
         if(rt.suf.length() > limlen)
             rt.overflow = true, rt.suf = rt.suf.substr(rt.suf.size() - limlen, rt.suf.size());
     } else rt.suf = b.suf;

     string s = a.suf + b.pre;
     for(int i = ; i < s.length(); i++)
         for(int j = , t = ; j < limlen && i + j < s.length(); j++) {
             t = (t << ) | (s[i + j] & );
             rt.mark[t | ( << (j + ))] = ;
         }

     int i;
     for(rt.rt = ; ; rt.rt++) {
         for(i = ; i < ( << rt.rt + ) && rt.mark[i | ( << rt.rt + )]; i++);
         if(!rt.mark[i | ( << rt.rt + )])
             break;
     }
     return rt;
 }

 int n, m;
 String strs[];

 inline void init() {
     cin >> n;
     for(int i = ; i <= n; i++) {
         cin >> strs[i].pre;
         strs[i].suf = strs[i].pre;
         strs[i].mark[] = ;
         for(int j = ; j < strs[i].pre.length(); j++)
             for(int k = , t = ; k < limlen && j + k < strs[i].pre.length(); k++) {
                 t = (t << ) | (strs[i].pre[j + k] & );
                 strs[i].mark[t | ( << (k + ))] = ;
             }
     }
 }

 inline void solve() {
     cin >> m;
     for(int i = , a, b; i <= m; i++) {
         cin >> a >> b;
         strs[n + i] = strs[a] + strs[b];
         cout << strs[n + i].rt << endl;
     }
 }

 int main() {
     ios::sync_with_stdio(false), cin.tie(), cout.tie();
     init();
     solve();
     return ;
 }