对《禁忌搜索(Tabu Search)算法及python实现》的修改
这个算法是在听北大人工智能mooc的时候，老师讲的一种局部搜索算法，可是举得例子不太明白。搜索网页后，发现《禁忌搜索(Tabu Search)算法及python实现》（https://blog.csdn.net/adkjb/article/details/81712969） 已经做了好详细的介绍，仔细看了下很有收获。于是想泡泡代码，看前面还好，后边的代码有些看不懂了，而且在函数里定义函数，这种做法少见，并且把函数有当作类来用，为什么不直接用类呢。还有就是，可能对禁忌搜索不太了解，可能具体算法在代码里有问题，欢迎提出。
import random class Tabu:
def __init__(self,tabulen=100,preparelen=200):
self.tabulen=tabulen
self.preparelen=preparelen
self.city,self.cityids,self.stid=self.loadcity2() #我直接把他的数据放到代码里了 self.route=self.randomroute()
self.tabu=[]
self.prepare=[]
self.curroute=self.route.copy()
self.bestcost=self.costroad(self.route)
self.bestroute=self.route
def loadcity(self,f="d:/Documents/code/aiclass/tsp.txt",stid=1):
city = {}
cityid=[] for line in open(f):
place,lon,lat = line.strip().split(" ")
city[int(place)]=float(lon),float(lat) #导入城市的坐标
cityid.append(int(place))
return city,cityid,stid
def loadcity2(self,stid=1):
city={1: (1150.0, 1760.0), 2: (630.0, 1660.0), 3: (40.0, 2090.0), 4: (750.0, 1100.0),
5: (750.0, 2030.0), 6: (1030.0, 2070.0), 7: (1650.0, 650.0), 8: (1490.0, 1630.0),
9: (790.0, 2260.0), 10: (710.0, 1310.0), 11: (840.0, 550.0), 12: (1170.0, 2300.0),
13: (970.0, 1340.0), 14: (510.0, 700.0), 15: (750.0, 900.0), 16: (1280.0, 1200.0),
17: (230.0, 590.0), 18: (460.0, 860.0), 19: (1040.0, 950.0), 20: (590.0, 1390.0),
21: (830.0, 1770.0), 22: (490.0, 500.0), 23: (1840.0, 1240.0), 24: (1260.0, 1500.0),
25: (1280.0, 790.0), 26: (490.0, 2130.0), 27: (1460.0, 1420.0), 28: (1260.0, 1910.0),
29: (360.0, 1980.0)} #原博客里的数据
cityid=list(city.keys())
return city,cityid,stid
def costroad(self,road):
#计算当前路径的长度 与原博客里的函数功能相同
d=-1
st=0,0
cur=0,0
city=self.city
for v in road:
if d==-1:
st=city[v]
cur=st
d=0
else:
d+=((cur[0]-city[v][0])**2+(cur[1]-city[v][1])**2)**0.5 #计算所求解的距离，这里为了简单，视作二位平面上的点，使用了欧式距离
cur=city[v]
d+=((cur[0]-st[0])**2+(cur[1]-st[1])**2)**0.5
return d
def randomroute(self):
#产生一条随机的路
stid=self.stid
rt=self.cityids.copy()
random.shuffle(rt)
rt.pop(rt.index(stid))
rt.insert(0,stid)
return rt
def randomswap2(self,route):
#随机交换路径的两个节点
route=route.copy()
while True:
a=random.choice(route)
b=random.choice(route)
if a==b or a==1 or b==1:
continue
ia=route.index(a)
ib=route.index(b)
route[ia]=b
route[ib]=a
return route
def step(self):
#搜索一步路找出当前下应该搜寻的下一条路
rt=self.curroute i=0
while i<self.preparelen: #产生候选路径
prt=self.randomswap2(rt)
if int(self.costroad(prt)) not in self.tabu: #产生不在禁忌表中的路径
self.prepare.append(prt.copy())
i+=1
c=[]
for r in self.prepare:
c.append(self.costroad(r))
mc=min(c)
mrt=self.prepare[c.index(mc)] #选出候选路径里最好的一条
if mc<self.bestcost:
self.bestcost=mc
self.bestroute=mrt.copy() #如果他比最好的还要好，那么记录下来
self.tabu.append(mc)#int(mrt)) #这里本来要加 mrt的 ，可是mrt是路径，要对比起来麻烦，这里假设每条路是由长度决定的
#也就是说 每个路径和他的长度是一一对应，这样比对起来速度快点，当然这样可能出问题，更好的有待研究
self.curroute=mrt #用候选里最好的做下次搜索的起点
self.prepare=[]
if len(self.tabu)>self.tabulen:
self.tabu.pop(0)
下面跑跑看：
import timeit
t=Tabu()print('ok')
print(t.city)
print(t.route)
print(t.bestcost)
print(t.curroute)
for i in range(1000):
t.step()
if i%50==0:
print(t.bestcost)
print(t.bestroute)
print(t.curroute) print('ok')
#print(timeit.timeit(stmt="t.step()", number=1000,globals=globals()))
print('ok')
ok
{1: (1150.0, 1760.0), 2: (630.0, 1660.0), 3: (40.0, 2090.0), 4: (750.0, 1100.0), 5: (750.0, 2030.0), 6: (1030.0, 2070.0), 7: (1650.0, 650.0), 8: (1490.0, 1630.0), 9: (790.0, 2260.0), 10: (710.0, 1310.0), 11: (840.0, 550.0), 12: (1170.0, 2300.0), 13: (970.0, 1340.0), 14: (510.0, 700.0), 15: (750.0, 900.0), 16: (1280.0, 1200.0), 17: (230.0, 590.0), 18: (460.0, 860.0), 19: (1040.0, 950.0), 20: (590.0, 1390.0), 21: (830.0, 1770.0), 22: (490.0, 500.0), 23: (1840.0, 1240.0), 24: (1260.0, 1500.0), 25: (1280.0, 790.0), 26: (490.0, 2130.0), 27: (1460.0, 1420.0), 28: (1260.0, 1910.0), 29: (360.0, 1980.0)}
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 19, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 3, 13, 23, 5]
24651.706120672443
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 19, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 3, 13, 23, 5]
21567.36269967159
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 3, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 19, 13, 23, 5]
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 3, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 19, 13, 23, 5]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 8, 27, 23, 7, 25, 15, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 27, 8, 23, 7, 25, 19, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 5, 9, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 3, 29, 26, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 8, 27, 23, 7, 25, 19, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 27, 8, 23, 7, 25, 19, 4, 13, 24]
9248.522952771107
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 29, 3, 26, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 15, 4, 13, 16, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 29, 3, 26, 21, 2, 20, 10, 18, 17, 14, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 26, 29, 3, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
看到最小路径是9213.89 如果我们把timeit去掉，跑1000步我的电脑是不到4秒大概
为了直观把路径画下来：
from matplotlib import pyplot x=[]
y=[]
print("最优路径长度:",t.bestcost)
for i in t.bestroute:
x0,y0=t.city[i]
x.append(x0)
y.append(y0)
x.append(x[0])
y.append(y[0])
pyplot.plot(x,y)
pyplot.scatter(x,y)
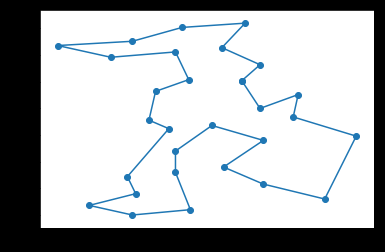
貌似找到最好的了。。。。
再跑一次：
9760.12
再来一次：
10212
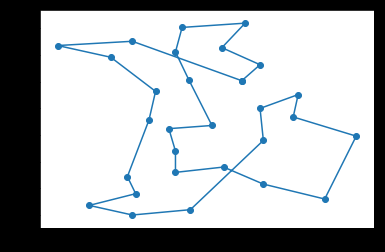
10500
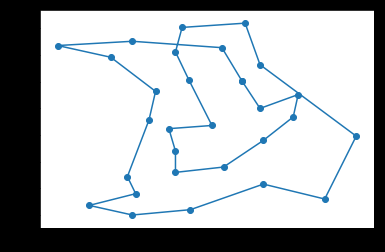
10100
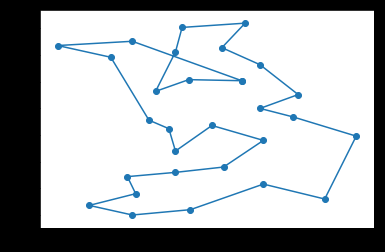
10080
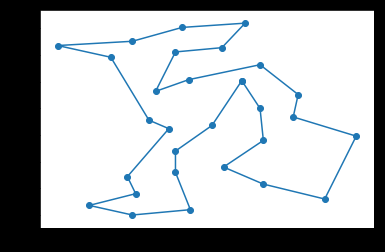
发现有些地方总有不变的地方，是不是可以把多条线路给叠加起来，做个链接的加权图，按照路径的权再来启发，是否能得到更好的结果呢？
比如右下角，一直都是一个形状，是否说明，这几个点的连接状况固定了呢？
这样可以把总是连续的点给合并成一个整体再来搜索是否也是个办法？
CSDN我的博客不知道怎么给禁用了，不能留言给博主，只能这样了。
对《禁忌搜索(Tabu Search)算法及python实现》的修改的更多相关文章
- 采用梯度下降优化器(Gradient Descent optimizer)结合禁忌搜索(Tabu Search)求解矩阵的全部特征值和特征向量
[前言] 对于矩阵(Matrix)的特征值(Eigens)求解,采用数值分析(Number Analysis)的方法有一些,我熟知的是针对实对称矩阵(Real Symmetric Matrix)的特征 ...
- 【算法】禁忌搜索算法(Tabu Search，TS)超详细通俗解析附C++代码实例
01 什么是禁忌搜索算法? 1.1 先从爬山算法说起 爬山算法从当前的节点开始,和周围的邻居节点的值进行比较. 如果当前节点是最大的,那么返回当前节点,作为最大值 (既山峰最高点):反之就用最高的邻居 ...
- MIP启发式求解：局部搜索 (local search)
*本文主要记录和分享学习到的知识,算不上原创. *参考文献见链接. 本文讲述的是求解MIP问题的启发式算法. 启发式算法的目的在于短时间内获得较优解. 个人认为局部搜索(local search)几乎 ...
- LeetCode初级算法的Python实现--排序和搜索、设计问题、数学及其他
LeetCode初级算法的Python实现--排序和搜索.设计问题.数学及其他 1.排序和搜索 class Solution(object): # 合并两个有序数组 def merge(self, n ...
- C++实现禁忌搜索解决TSP问题
C++实现禁忌搜索解决TSP问题 使用的搜索方法是Tabu Search(禁忌搜索) 程序设计 1) 文件读入坐标点计算距离矩阵/读入距离矩阵 for(int i = 0; i < CityNu ...
- 选择性搜索(Selective Search)
1 概述 本文牵涉的概念是候选区域(Region Proposal ),用于物体检测算法的输入.无论是机器学习算法还是深度学习算法,候选区域都有用武之地. 2 物体检测和物体识别 物体识别是要分辨出图 ...
- 常用查找数据结构及算法（Python实现）
目录 一.基本概念 二.无序表查找 三.有序表查找 3.1 二分查找(Binary Search) 3.2 插值查找 3.3 斐波那契查找 四.线性索引查找 4.1 稠密索引 4.2 分块索引 4.3 ...
- 集束搜索beam search和贪心搜索greedy search
贪心搜索(greedy search) 贪心搜索最为简单,直接选择每个输出的最大概率,直到出现终结符或最大句子长度. 集束搜索(beam search) 集束搜索可以认为是维特比算法的贪心形式,在维特 ...
- 第三十三节，目标检测之选择性搜索-Selective Search
在基于深度学习的目标检测算法的综述 那一节中我们提到基于区域提名的目标检测中广泛使用的选择性搜索算法.并且该算法后来被应用到了R-CNN,SPP-Net,Fast R-CNN中.因此我认为还是有研究的 ...
随机推荐
- 利用awk处理学生成绩问题（难度较大）
学生成绩表单如下: Name,Team,First Test, Second Test, Third Test Tom,Red,,, Joe,Green,,, Maria,Blue,,, Fred,B ...
- 准备下上机考试，各种排序！！以后再添加和仿真像wiki上那样！
#include <stdio.h> #include <string.h> #define N 6 typedef struct { ]; int score; }stude ...
- SQL-33 创建一个actor表，包含如下列信息
题目描述 创建一个actor表,包含如下列信息 列表 类型 是否为NULL 含义 actor_id smallint(5) not null 主键id first_name varchar(45) ...
- Python3虚拟环境安装:virtualenv、virtualenvwralpper
一:通过pip3(因python2和3共存,前文修改过pip3软连接,pip3可以安装到python3)安装virtualenv,pip3 install virtuale 二:建立虚拟环境文件目录 ...
- Android开发 ---基本UI组件2：图像按钮、单选按钮监听、多选按钮监听、开关
Android开发 ---基本UI组件2 1.activity_main.xml 描述: 定义一个按钮 <?xml version="1.0" encoding=" ...
- innodb mvcc，事务隔离级别，读写锁
mvcc其实和copyonwritelist的思路差不多:读不加锁,写加锁,事务提交之后释放锁,并且延伸的是,在UNdolog里面保存了几个版本,实现不同的隔离级别.如果读数据页里面最新的数据,那么就 ...
- L317 电子烟
Why it’s so hard to talk about e-cigarette risks A growing proportion of American adults consider va ...
- Tensorflow函数：tf.zeros
tf.zeros函数 tf.zeros( shape, dtype=tf.float32, name=None ) 定义在:tensorflow/python/ops/array_ops.py. 创建 ...
- Git客户端的安装与配置入门
GitLab与Git客户端的安装与配置入门,每次配置完一段时间,就忘记配置过程了,为了自己和同学们以后有所参照,特记录了本次下载和配置,其实Git就是一个版本控制系统,类似于SVN,CVS等 下载:W ...
- elasticsearch学习笔记——安装，初步使用
前言 久仰elasticsearch大名,近年来,fackbook,baidu等大型网站的搜索功能均开始采用elasticsearch,足见其在处理大数据和高并发搜索中的卓越性能.不少其他网站也开始将 ...