POJ 1470 Closest Common Ancestors

传送门

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 17306		Accepted: 5549

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ...

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
For example, for the following tree: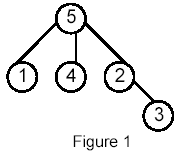 

Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

Source

Southeastern Europe 2000

-----------------------------------------------------------------------

LCA

采用 Tarjan 离线 LCA 算法比较方便

注意读入细节

-------------------------------------------------------------------------

#include <cstdio>
#include <vector>
#include <cstring>
#define pb push_back

using namespace std;
const int N();
vector<int> q[N], g[N];
int par[N], ans[N], col[N];
int find(int u){return par[u]==u?u:find(par[u]);}
void dfs(int u, int f){
	col[u]=-;
	for(int i=; i<q[u].size(); i++){
		int &v=q[u][i];
		if(col[v]==-) ans[v]++;
		else if(col[v]==) ans[find(v)]++;
		else q[v].pb(u);
	}
	for(int i=; i<g[u].size(); i++){
		int &v=g[u][i];
		dfs(v, u);
	}
	col[u]=;
	par[u]=f;
}
int main(){
	//freopen("in", "r", stdin);
	int n, m, u, v;
	for(;~scanf("%d", &n);){
		for(int i=; i<=n; i++) g[i].clear(), q[i].clear();
		memset(par, , sizeof(par));
		for(int i=; i<n; i++){
			scanf("%d:(%d)", &u, &m);
			while(m--){
				scanf("%d", &v);
				par[v]=u;
				g[u].pb(v);
			}
		}
		scanf("%d", &m);
		while(m--){
			scanf(" (%d%d)", &u, &v);
			q[u].pb(v);
		}
		int rt;
		for(rt=; par[rt]; rt=par[rt]);
		for(int i=; i<=n; i++) par[i]=i;
		memset(ans, , sizeof(ans));
		memset(col, , sizeof(col));
		dfs(rt, rt);
		for(int i=; i<=n; i++) if(ans[i]) printf("%d:%d\n", i, ans[i]);
	}
}