[bzoj1007][HNOI2008]水平可见直线_单调栈

水平可见直线 bzoj-1007 HNOI-2008

　　　　题目大意：给你n条直线，为你从上往下看能看见多少跳直线。

　　　　注释：能看见一条直线，当且仅当这条直线上存在一条长度>0的线段使得这条线段上方没有其他直线，$1\le n 5\cdot 10^4$。

　　　　　　想法：神题qwq。看见网上的做法突然有一种学计算几何的冲动，直到看见一篇大神的blog说用单调栈做？这题困难其实就困难在如何规定两条直线之间本不存在的单调性。用单调栈就是讲即将进栈元素不断和栈顶比较，然后弹来弹去最后剩下的都是可见的。不容易难想到：将直线先按斜率排序。如果两直线斜率相等那么截距小的那个自然直接gg。

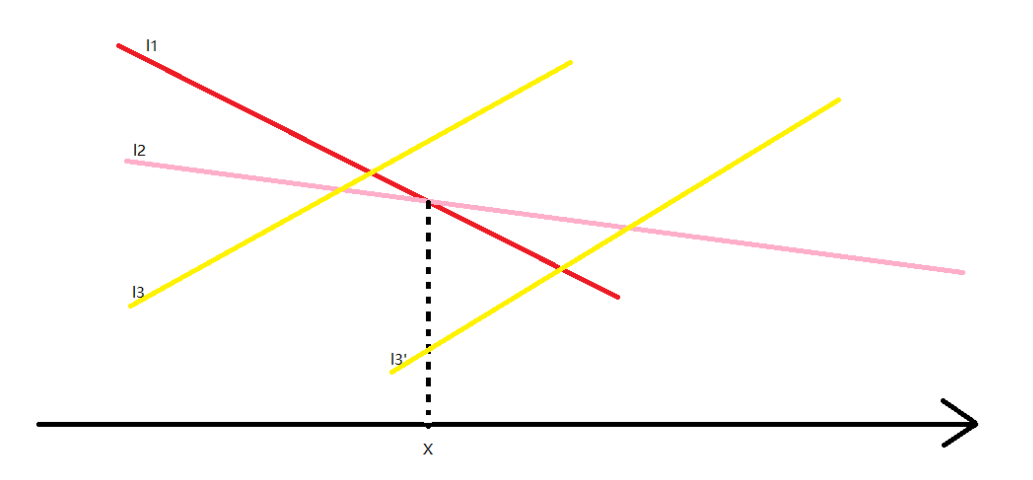
　　　　　　显然，当待入栈直线和栈顶直线的交点直接决定了栈顶直线是否仍有存在的意义。如果$l_3$和$l_2$的交点在x左侧，那么显然，$l_2$就可以滚犊犊了。以此类推，即可。

　　　　最后，附上丑陋的代码... ...

#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 1000010
using namespace std;
struct Node
{
	double k,b;
	int id;
}l[N];
inline bool cmp(Node a,Node b)
{
	if(a.k!=b.k) return a.k<b.k;
	return a.b>b.b;
}
double getpos(Node a,Node b)
{
	return (b.b-a.b)/(a.k-b.k);
}
int s[N];
bool ans[N];
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lf%lf",&l[i].k,&l[i].b);
		l[i].id=i;
	}
	sort(l+1,l+1+n,cmp);
	int top=1;
	s[1]=1;
	for(int i=2;i<=n;i++)
	{
		if( l[i].k-l[i-1].k < 1e-8) continue;
		while(top > 1&& getpos(l[i],l[s[top]])  <= getpos(l[s[top]],l[s[top-1]]) ) top--;
		s[++top]=i;
	}
	for(int i=1;i<=top;i++) ans[l[s[i]].id]=1;
	for(int i=1;i<=n;i++)
	{
		if(ans[i])
		{
			printf("%d ",i);
		}
	}
	puts("");
	return 0;
}

　　　　小结：对于这种问题将已知的元素排序，并将它们强行化作单调的情况，是不必要但可行的。