Intersection between a 2d line and a conic in OpenCASCADE

Intersection between a 2d line and a conic in OpenCASCADE

eryar@163.com

Abstract. OpenCASCADE provides the algorithm to implementation of the analytical intersection between a 2d line and another conic curve. The conic is defined by its implicit quadaratic equation, so the intersection problem is become a polynomial roots finding problem. The paper focus on the 2d line intersection another conic algorithm implementation.

Key Words. 2d line intersection, conic

1.Introduction

高中的时候学习了直线Line、圆Circle、圆锥曲线Conic（椭圆Ellipse、双曲线Hyperbola和抛物线parabola）等二维曲线的方程及特性，也可以对他们之间的相交情况进行计算。如何编程实现直线与任意圆锥曲线相交呢？本文通过对OpenCASCADE中二维直线与圆锥曲线相交代码的分析来理解其实现原理。

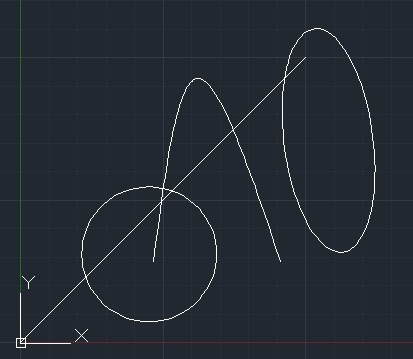
Figure 1. 直线与圆锥曲线相交

对于二维曲线知识的学习又把思绪拉回到高中年代，翻开泛黄的课本，遥想那个青涩时候，对于《数学》的学习也是停留在解题上，没有理解，更别说应用了。有人说数学、英语和代码是当今的世界语言，都可以进行思想的交流。数学本来就是描述现实世界规律的精妙语言，但我终究是个俗人，更崇拜能应用数学创建价值的人，如OpenCASCADE的开发者们。

2.Conic Implicit Equation

圆锥曲线一般的代数表示方法为：

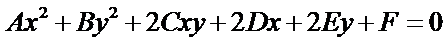
OpenCASCADE中使用类IntAna2d_Conic来表示圆锥曲线的代数方程。并提供了将二维曲线（直线、圆、椭圆、抛物线、双曲线）转换成代数方程的方法，相关代码如下所示：

Code highlighting produced by Actipro CodeHighlighter (freeware)
http://www.CodeHighlighter.com/

-->IntAna2d_Conic::IntAna2d_Conic (const gp_Lin2d& L) {
  a = 0.0;
  b = 0.0;
  c = 0.0;
  L.Coefficients(d,e,f);
  f = 2*f;
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Circ2d& C) {
  C.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Elips2d& E) {
  E.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Parab2d& P) {
  P.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Hypr2d& H) {
  H.Coefficients(a,b,c,d,e,f);
}

3.Intersection Implementation

当对直线和圆锥曲线进行求交时，先得到了直线的一般式方程和圆锥曲线的一般式方程，将它们联立成方程组如下所示：

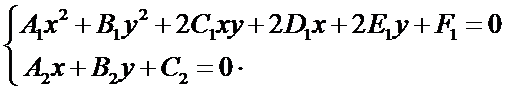
是一个二元二次方程组。通过直线的参数表示法，将上述二元二次方程组转换成一元二次方程，再对这个方程进行求解。设直线l经过点P0(x0,y0)，v=(a, b)是它的一个方向向量。P(x,y)是直线上任意一点，则向量P0P与v共线。根据向量共线的充要条件，存在唯一实数t，使：

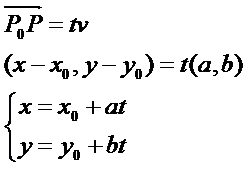
将直线的一般式化为参数式为：

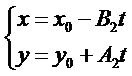
将直线的参数式代入圆锥曲线的一般式得到：

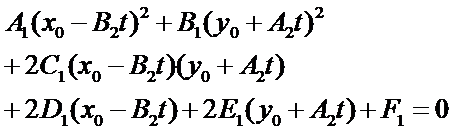
整理上述方程得：

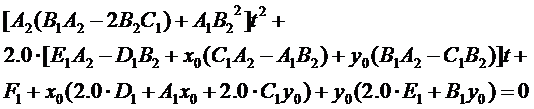
得到各次系数后，就可以用Newton法来解这个一元二次方程了。OpenCASCADE中的实现代码如下所示：

Code highlighting produced by Actipro CodeHighlighter (freeware)
http://www.CodeHighlighter.com/

-->void IntAna2d_AnaIntersection::Perform (const gp_Lin2d& L,
                   const IntAna2d_Conic& Conic)
{
  Standard_Real A,B,C,D,E,F;
  Standard_Real px0,px1,px2;
  Standard_Real DR_A,DR_B,DR_C,X0,Y0;
  Standard_Integer i;
  Standard_Real tx,ty,S;
  
  done = Standard_False;
  nbp  = 0;
  para = Standard_False;
  iden = Standard_False;
 
  Conic.Coefficients(A,B,C,D,E,F);
  L.Coefficients(DR_A,DR_B,DR_C);
  X0=L.Location().X();
  Y0=L.Location().Y();
  
  // Parametre: L
  // X = Xo - L DR_B    et     Y = Yo + L DR_A

px0=F + X0*(D+D + A*X0 + 2.0*C*Y0) + Y0*(E+E + B*Y0);
  px1=2.0*(E*DR_A - D*DR_B + X0*(C*DR_A - A*DR_B) + Y0*(B*DR_A - C*DR_B));
  px2=DR_A*(B*DR_A - 2.0*C*DR_B) + A*(DR_B*DR_B);
  
  MyDirectPolynomialRoots Sol(px2,px1,px0);
  
  if(!Sol.IsDone()) {
    done=Standard_False;
    return;
  }
  else { 
    if(Sol.InfiniteRoots()) {
      iden=Standard_True;
      done=Standard_True;
      return;
    }
    nbp=Sol.NbSolutions();
    for(i=1;i<=nbp;i++) {
      S=Sol.Value(i);
      tx=X0 - S*DR_B;
      ty=Y0 + S*DR_A;
      lpnt[i-1].SetValue(tx,ty,S);
    }
    Traitement_Points_Confondus(nbp,lpnt);
  }
  done=Standard_True;
}

从上述源码可知，OpenCASCADE使用了直线的参数式来将直线与圆锥曲线的求交表示成一元二次方程，再使用Newton法来对方程进行求解。 其中变量px0、px1、px2分别表示一元二次方程的零次、一次和二次项的系数。

4.Conclusion

通过圆锥曲线的一般式和直线的参数式将直线与圆锥曲线相交问题变成一个一元二次方程的求根问题，再通过方程求根的Newton法来对一元二次方程进行求解。

5.References

1. 人民教育出版社中学数学室. 数学第二册上. 人民教育出版社. 2000

2. 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002

3. 李原, 张开富, 余剑峰. 计算机辅助几何设计技术及应用. 西北工业大学出版社. 2007

4. 丘维声. 解析几何. 北京大学出版社. 1996

PDF Version: Intersection between a 2d line and a conic in OpenCASCADE