深入理解:Linear Regression及其正则方法

　　这是最近看到的一个平时一直忽略但深入研究后发现这里面的门道还是很多,Linear Regression及其正则方法(主要是Lasso,Ridge, Elastic Net)这一套理论的建立花了很长一段时间,是很多很多人的论文一点点堆起来的一套理论体系.如果你只停留在知道简单的Linear Regression,Lasso, Ridge, Elastic Net的原理,没有深入了解这套理论背后的故事,希望你能从这篇博客中有所收获,当然博主水平有限,也只是稍微深入了一些,如果你是主要做这方面的工作,还望你找一些相关论文来深入学习.

　　对于常见的Linear Regression我们刚学机器学习的时候会感觉这套理论很简单,损失函数是一个均方误差损失,然后用梯度下降来找最优的系数w即可.无论是数学公式的推到还是代码实现都非常简答.于是很多人都开始了学习下一章,.对于Lasso和Ridge也就是常用的L1正则和L2正则可能有部分人理解起来稍微麻烦一点,网上的教程也很多有的写的也非常好.大家可以取参考一下.这里假设大家对于L1正则是为了让一些相关度低的特征系数变为0从而达到select variable的目的,L2正则是对特征进行shrankage从而让模型更加balance(模型中个特征的系数都很小,因此模型不会受到某几个strong feature的影响)都有所了解,对于Elastic Net估计大家都停留在知道其是L1和L2正则的综合,但是究竟其背后的原理估计没人去深究.这里我来讲讲这套理论的发展历史.从理论一步步建立的过程来让大家对这几个算法有更深入的理解,做到知其然,知其所以然.

　　首先Linear Regression刚出来的时候效果很好(因为当时数据量不大,计算机性能也不好,Linear Regression已经是比较好的模型)因此被广泛使用,但是基于均方误差损失函数的Linear Regression有一个致命问题就会预测结果l地偏差高方差这个是均方误差损失函数的问题同时模型的解释性会很差,在小规模数据集上还能忍受,但是随着时间的推移,数据量在急剧增大,面对大数据集情况下出现高方差.模型的泛化能力弱如何解决,人们为了解决这个问题提出了L2正则,我们都知道,均方误差损失函数下对于那种噪点的loss会很大(y因为有个平方项),如果噪点恰好在strong featrue上那个loss大家可以脑补一下.为此人们想到了shrankage就是压缩权重系数,这样不论数据偏差多大,每个特征的贡献都会很小,模型整体对于单个特征的依赖就会减弱,这样模型整体的方差就不会很大,但是压缩意味着强特征的效果弱化,自然而然使得bias有所增大,但是就像机器学习模型的经典理论trade off biase and variance一样在这两者中找到一个平衡就好.而压缩权重系数的重任就交给了L2正则,这也是L2正则的特点.因此Ridge Regression理论就建立起来了.参数调好的情况下,其效过确实优于Linear Regression当然也是有前提条件的,对于特征较多,且大部分特征的影响较少的数据集上表现会非常好(Ridge只是L2正则中一个非常经典的算法,后来人们也对其进行了一系列的扩展来让它适应其他情况比如group Ridge就是对特征分组然后压缩等).anyway L2解决了模型的准确率的问题但是可解释性依然没有得到解决,而且当时的计算机算力不行,特征多了计算起来非常费时间,于是人们又开始了新算法的研究之路,这个研究的目的很明确就是来完成L2正则未完成的任务将一些特征压缩到0,这样模型实际用到的特征会很少可解释性得到满足同时计算速度也会大幅提高,当然其具体过程也是一波三折,大家可以仔细研究研究相关论文,最后提出来了L1正则,其思路是尽量把一些特征压缩到0,这样很显然模型的预测biase会变大一些,但是模型的variance会降低,同时计算速度会提高很多而且最重要的是模型的解释性能会变得很强(因为特征少了).因此在一些情况下也广泛使用(使用条件:小到中等数量的特征中等大小影响的数据集上表现比较好).这里说点题外话,在这两个算法提出来之前,人们进行特征选择是用subset selection来做的,就是暴力搜索,找出K个最优特征的组合,这种方法计算起来非常慢(当时人们提出来贪心来加速找近似最优解).所以我们从这个算法的发展过程可以看出来,算法的发展一定是在解决实际问题的基础上一步步演变的,非常有趣.

　　最后就是L1和L2正则结合的elastic net了,这个算法克服了Lasso在一些场景的限制:

　　(1)当P>>N(p是特征N是数据量)时Lasso最多只能选N(为什么是N需要用矩阵的知识来简单证明一下)个个特征这显然不是非常合理.

　　(2)当某些特征的相关性非常高,也就是所谓的组变量,Lasso一般倾向于只选择其中的一个也不关心究竟要选哪一个

　　(3)对于一般N>P的情况,如果某些特征与预测值之间的相关性很高,经验证明预测的最终性能是Lasso占主导地位相比于Ridge

　　对于上述三个缺陷,人们就提出来Elastic Net.其思想还是建立在L1正则上面的,其目的是在保证Lasso的优良特性的情况下,克服其缺项.Elastic Net既能select variable同时也能shrankage.他能同时选择相关度很高的组变量.论文上的一个比喻很形象:Elastic Net像一个可伸缩的渔网,可以网住所有的大鱼.这个算法的优化也有一些门道,传统的思路其实比较容易想到对于一个加了L1和L2正则的均方误差损失函数,我们先固定λ₂(L2正则项的系数)对所有的权重进行压缩,完成L2正则,然后用Lasso进行压缩,进行特征选择.但是这种方法有一个很致命的缺陷就是很慢,相当于要进行两次正则计算非常耗时.同时这种两次压缩并没有根本减少方差同时还引入了额外的偏差所以这种方法也叫作naive Elastic Net.后来为了优化这个算法又提出了最终我们目前使用的Elastic Net,其思想也很简单,但是很巧,就是将L2正则项同均方误差项进行合并,这样L2正则这一步就直接去掉相当于变成一个权重系数的缩减,因此这个新的表达式就可以近似看成一个Lasso Regression了.这样整个算法的计算时间跟Lasso一样,同时也避免了两次shrankage带来的额外偏差.当然整个算法具体实现细节需要大量的数学证明.这里就一一略过,需要深入了解的可以看看论文,写的很详细.

　　这里我对Linear Regression及其正则的实际使用发展历史及每个算法要解决的问题进行了一一阐述,可能有些粗糙.但是相信大家对于整个算法的发展过程有了了解后也明白什么样的情况使用什么样的算法,以及各个算法的局限性.下面我来做几个简单的实验demo来看看上面几个算法的效果,主要使用sklearn.

　　

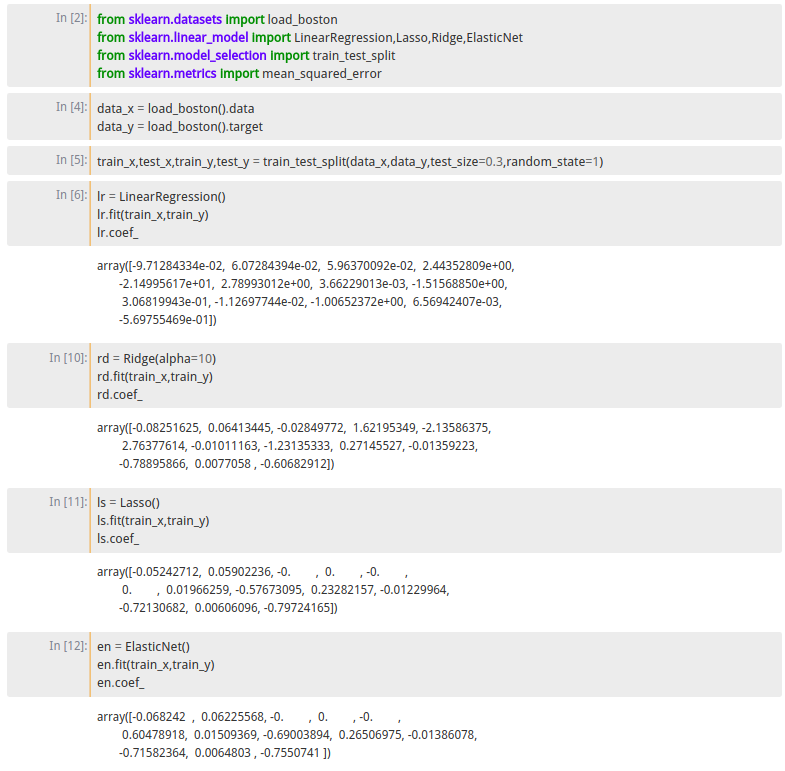
　　这里的数据集直接使用的是sklearn自带的boston房价数据集,其中特征较少,效果可能没那么明显,但整体来看还是有明显区别,其中lr是LinearRegression模型,其训练模型的系数差异很大,系数的大小代表个特征的权重,特征的强弱关系非常明显.有些特征很强有些很弱.接下来是rd表示Ridge模型(我把惩罚因子alpha稍微调大了一点效果更加明显),可以看出来相比如lr模型其系数都不同程度的进行了压缩,如果我们把alpha继续调大效果会更加明显,当然我这里没有管最终的预测结果,只是让大家感受一下这几个正则的效果.接着看ls表示Lasso模型相比如lr模型其及进行的shrankage同时也进行了变量选择.因为有四个特征的系数变为了0.最后我们看Elastic Net模型相比如Lasso模型其压缩幅度没有那么大,因此只有三个变量被压缩为0.这里看Elastic Net可能效果很差,但是不代表Elastic Net没有用,使用时我们一定要搞清楚自己的数据集的特点,每种数据集主要面对的是什么问题,才能找到最合适的方法.

　　通过上面的一个简单例子我们可以感受一下各种正则压缩的效果,当然如果纯粹从性能角度来看,我们需要用大量不同数据集来测试,如果大家有兴趣可以找一些数据集来测试一下各种算法的具体效果.这里对于Linear regresion及其正则方法有了一个全面的介绍,也给出了各种算法适合的条件和个算法解决的问题.实际问题中如何使用这些算法,还需要根据具体数据具体问题来分析选取.希望这篇简短的介绍能给大家对Linear regression更深刻的认识.