Python Linear algebra

Linear algebra

1.模块文档

NAME
    numpy.linalg
DESCRIPTION
    Core Linear Algebra Tools
    -------------------------
    Linear algebra basics:

    - norm            Vector or matrix norm
    - inv             Inverse of a square matrix
    - solve           Solve a linear system of equations
    - det             Determinant of a square matrix
    - lstsq           Solve linear least-squares problem
    - pinv            Pseudo-inverse (Moore-Penrose) calculated using a singular
                      value decomposition
    - matrix_power    Integer power of a square matrix

    Eigenvalues and decompositions:

    - eig             Eigenvalues and vectors of a square matrix
    - eigh            Eigenvalues and eigenvectors of a Hermitian matrix
    - eigvals         Eigenvalues of a square matrix
    - eigvalsh        Eigenvalues of a Hermitian matrix
    - qr              QR decomposition of a matrix
    - svd             Singular value decomposition of a matrix
    - cholesky        Cholesky decomposition of a matrix

    Tensor operations:

    - tensorsolve     Solve a linear tensor equation
    - tensorinv       Calculate an inverse of a tensor

    Exceptions:

    - LinAlgError     Indicates a failed linear algebra operation

LA.info?
Type:        module
String form: <module 'numpy.linalg.info' from 'F:\\Anaconda3\\lib\\site-packages\\numpy\\linalg\\info.py'>
File:        f:\anaconda3\lib\site-packages\numpy\linalg\info.py
Docstring:
Core Linear Algebra Tools
-------------------------
Linear algebra basics:

- norm            Vector or matrix norm
- inv             Inverse of a square matrix
- solve           Solve a linear system of equations
- det             Determinant of a square matrix
- lstsq           Solve linear least-squares problem
- pinv            Pseudo-inverse (Moore-Penrose) calculated using a singular
                  value decomposition
- matrix_power    Integer power of a square matrix

Eigenvalues and decompositions:

- eig             Eigenvalues and vectors of a square matrix
- eigh            Eigenvalues and eigenvectors of a Hermitian matrix
- eigvals         Eigenvalues of a square matrix
- eigvalsh        Eigenvalues of a Hermitian matrix
- qr              QR decomposition of a matrix
- svd             Singular value decomposition of a matrix
- cholesky        Cholesky decomposition of a matrix

Tensor operations:

- tensorsolve     Solve a linear tensor equation
- tensorinv       Calculate an inverse of a tensor

Exceptions:

- LinAlgError     Indicates a failed linear algebra operation

2.可用方法

'bench','cholesky','cond','det','division','eig','array','eigh','eigvals','eigvalsh','info','inv','lapack_lite','linalg','lstsq','matrix_power','matrix_rank','multi_dot','norm','pinv','print_function','qr','slogdet','solve','svd','tensorinv','tensorsolve','test'
eig : eigenvalues and right eigenvectors of general arrays
    eigvalsh : eigenvalues of symmetric or Hermitian arrays.
    eigh : eigenvalues and eigenvectors of symmetric/Hermitian arrays.

3.常用方法

首先导入相关模块

import numpy as np
from numpy import linalg as LA

3.1求数组的行列式：det

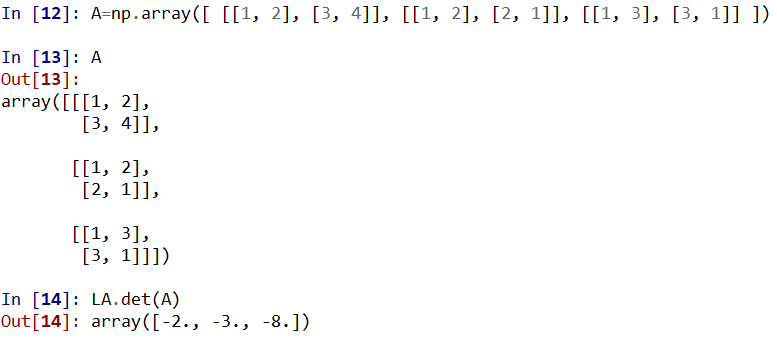
3.2求方阵的特征值、特征向量：eig

3.3求方阵的逆矩阵:：inv

3.4求解线性方程组：solve

Solve the system of equations 3 * x0 + x1 = 9 and x0 + 2 * x1 = 8:

3.5一个方阵的整数次幂：matrix_power

3.6计算在一个函数调用两个或两个以上的阵列的点积：multi_dot

4.官网文档

https://docs.scipy.org/doc/numpy/reference/routines.linalg.html