POJ 2184 Cow Exhibition (01背包的变形)

本文转载，出处：http://www.cnblogs.com/Findxiaoxun/articles/3398075.html

很巧妙的01背包升级。看完题目以后很明显有背包的感觉，然后就往背包上靠。把s看成是空间，f看成是价值，转换成了01背包经典模型(没有想到，，，)。可，s是负值，这就涉及到一个问题，如果按照普通的01背包，(01背包的倒序原因请参看这个http://hi.baidu.com/findxiaoxun/item/9abf560127a155c091571868)

for(int i=;i<n;i++)
    for(int v=maxv;v>=vi[i];v--)
        dp[v]=max{dp[v],dp[v-vi[i]]+w[i]}

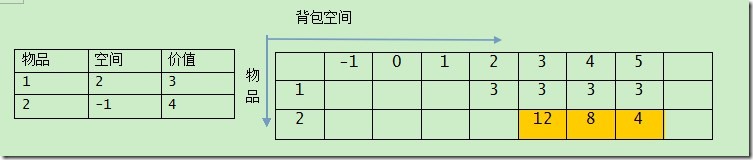
循环物品的时候，看第一件，在此题中，我们先假设最大空间为5，则2->5的值都为3，

然后i=1,循环第二件，v=5->3,而dp[5]=max{dp[5],dp[5+1]+4}，背包空间为6的位置，我们假设预置为0，则dp[5]=4;dp[4]=max{dp[4],dp[4-(-1)]+4};则dp[4]=4+4=8;其实到这个值，我们已经看出，如果按照正常的逆序，s为负值的物品不只使用一次，这与题目的要求是相悖的。那么，正序考虑。读者可以自行推导，证明其可行性。

而我们发现，背包空间出现了负值，下限是-100*1000；上限是100*1000；一个很容易想到的方法就是，把100*1000，作为我们的数轴上的0点。也就是背包空间变成2*100*1000，不过在考虑的时候，以100*1000为原点，左边实际上是负值，右边是正值。则dp[i]是数据中左边一列s的和为s时的最大f值，而s+f=dp[i]+i-10000;

初始预置为-INF，dp[orgpoint]=0的目的是为了从0原点开始，而且，只放可以放的点。用一两个样例思考下就能明白。

算法的可行性，其实最大的要求就是符合01背包的特点，每个物品后只有一件，只放一次。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int MAXN=;
const int INF=0x3f3f3f3f;
const int MAXV=*(int)1e5;
int dp[MAXV+];
int s[MAXN],f[MAXN];
int n;
int main(){
    int orgpoint=(int)1e5;
    while(scanf("%d",&n)!=EOF){
        for(int i=;i<n;i++)scanf("%d%d",&s[i],&f[i]);
        for(int i=;i<=MAXV;i++)dp[i]=-INF;
        dp[orgpoint]=;
        for(int i=;i<n;i++){
            if(s[i]>){//>0 then in reversed order
                for(int j=MAXV;j>=s[i];j--)//this order ensure that we put every item just for one time
                     if(dp[j-s[i]]>-INF)
                        dp[j]=max(dp[j],dp[j-s[i]]+f[i]);
            }else{//if negative number,have a look at the proof
                for(int j=;j<MAXV+s[i];j++)
                    if(dp[j-s[i]]>-INF)
                        dp[j]=max(dp[j],dp[j-s[i]]+f[i]);
            }
        }
        int ans=;
        for(int i=;i<=;i++)
            if(dp[i]>=&&dp[i]+i->ans)
                ans=dp[i]+i-;
        printf("%d\n",ans);

    }
return ;
}

代码参考http://www.cnblogs.com/kuangbin/archive/2012/09/14/2684929.html

最后附上本人的代码，其实差不多啦：

#include <iostream>
#include <stdio.h>
#include <string.h>
/*
AC
*/
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=;
const int V=;
int s[maxn],f[maxn];
int dp[V*+];
int n;
int main()
{
    int a,b;
    int sum=;
    scanf("%d",&n);
    for(int i=;i<n;i++){
        scanf("%d%d",&a,&b);
        s[i]=a;
        f[i]=b;
    }
    //memset(dp,0,sizeof(dp));  //不能为0值。。。因为f[i]有小于0的值，应该取负无穷大的值
    for(int i=;i<V*+;i++)
        dp[i]=-INF;
    dp[V]=;
    for(int i=;i<n;i++){
        if(s[i]>=){
            for(int v=V*;v>=s[i];v--){   //倒叙
                dp[v]=max(dp[v],dp[v-s[i]]+f[i]);
            }
        }
        else{
            for(int v=;v<=V*;v++){  //正序
                dp[v]=max(dp[v],dp[v-s[i]]+f[i]);
            }
        }
    }
    for(int i=;i<=V*;i++){
        if(i-+dp[i]>sum && dp[i]>=){
            sum=i-+dp[i];
        }
    }
    printf("%d\n",sum);
    return ;
}