Leetcode基础篇30天30题系列之数组：模拟计算法

作者：丁宋涛

数组：加一

题干：

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储一个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

参考样例：

示例 1:

输入: [1,2,3]

输出: [1,2,4]

解释: 输入数组表示数字 123。

示例 2:

输入: [4,3,2,1]

输出: [4,3,2,2]

解释: 输入数组表示数字 4321。

这道题是一道数组的基础题，其本质是一道模拟计算题。

这道题有一定的工程应用意义，大家都知道，计算机的浮点数运算有误差，究其细节有相当数量的开发者却往往不求甚解。请看：

做开发的朋友都知道计算机在程序处理中，都是将十进制数转成二进制数进行运算的。对于这种转化，其方法就是除2逆向取余法，例如：

十进制数13转成二进制的方法就是

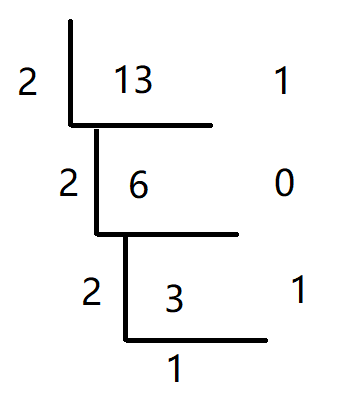
转化成数学表达式就是（13）₁₀=（1101）₂

对于十进制小数转化成二进制小数使用的方法是乘2正向取整法，比如十进制的0.75

即（0.75）₁₀=（0.11）₂

如果，我们考虑下将十进制的0.6转化成二进制呢？如果依然使用乘二正向取整法会发生什么呢？

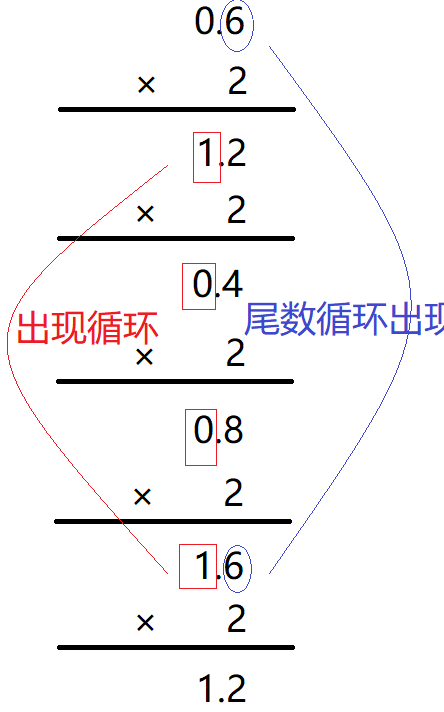
如果从数学上讲，（0.75）₁₀=（0.1001）₂

为什么会出现这种循环表示呢？因为数学上有证明，十进制表示法与二进制表示法，仅仅在整数范围内才有明确的对应的关系，而小数部分是做不到的。因此，在采用二进制运算上，计算机的数值求解是有缺陷的。

意识到这一点，我们就会问那么是不是我们现在和小数点相关的运行都是不可靠的呢？显然不可能，最常见的就是我们的金融活动。大凡和交易有关的数据，那是一个数字都不能出错的，那么他们背后的计算过程又是如何保证的呢？

答案就是模拟计算。

在小学数学课本上就教过这样的案例：123.4+5.67，我们来看，加数与被加数的位数并不相同，小学老师在教学中一定会强调对齐小数点，其过程如下：

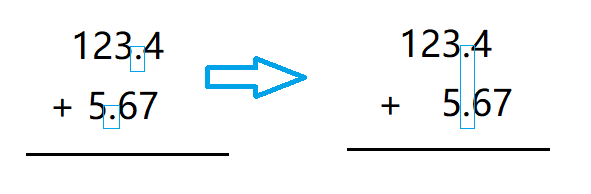
这个在计算机中有一个术语叫做对阶。所谓阶就是进制，十进制的阶就是10，二进制的阶就是2，具体的数学表达就是

123.4 = 1×10²+2×10¹+3×10⁰+4×10^-1

5.67=5×10⁰+6×10^-1+7×10^-2

我们知道计算机的整数运算是没有缺陷的，如果我们这样做，是不是就可以达到精确求解的目的了？

123.4+5.67=（12340+567）×10^-2=12907×10^-2=129.07

这就是精度计算中的常用的计算思想，这也是为什么在以Java为核心语言中做交易系统中，金额通常不用float，double而用decimal类型的原因。

明白了这个知识，我们就知道了这个看似普通的题目，其实是企业开发商用软件中的一个现实问题。那么，在现实计算中，人们又是如何来处理上述的对阶、运算的过程呢？答案就是数组。我们用数组来模拟每一位，然后用小学数学课本教授的方法，手工计算出就可以了。

下面回到这个题目：题目的函数签名是这样的：vector<int> plusOne(vector<int>& digits)

传入的参数是digits，是一个整型的向量，其位数按照角标升序排列，即角标0对应的是数字的最高位，最后一位表示的数字的最低位，比如参考样例：[1,2,3],他表示的是十进制123，角标0对应的是百位1，角标2对应的是个位3.模拟十进制计算的过程，就是逢10进位，这道题我们首先要找到最低位，如果最低位不是9，直接取出角标对应的数值加1即可，如果是数字的9的话，那么直接将其改为0，并向其上一位角标对应的数字加1.需要注意的细节是，如果这个数字恰好是[9,9,9],那么返回值应当增加1位得到[1,0,0,0]。为了方便编程，我们从最后一位开始。代码如下：

1 vector<int> plusOne(vector<int>& digits) {

2        int n = digits.size();

3        for(int i=n-1;i>=0;i--){

4            if(digits[i] == 9)

5                digits[i] =0;

6            else {

7                digits[i]++;

8                return digits;

9            }

10        }

11        digits[0] =1;

12        digits.push_back(0);

13        return digits;

14 }

第2行，首先获得当前向量digits的长度，并将其复制给n，然后从角标n-1开始，逆向遍历整个数组，由于i是从n-1开始，我们先判断当前位置是否是9，如果是9，那么就把把当前位置置0，并向前遍历到前一个位置，只要前一个位置不是9，那么就把此时的位置加1，然后返回。如果全体循环结束都没有返回，那么说明传入的必然是999这种类型的。那么出了循环之后，先把角标0改为1，并再增加一个0，就完成了全部的计算过程。